Crypto趣题-分组密码

这篇文章主要记录一些分组密码相关的趣题

EASY_dfa

最近做到的我觉得相当有意思的一个题，在这里记录一下解题过程

题目来源：川渝网络安全竞赛 2022

题目：

#!/usr/bin/python3
from random import sample, choice
from os import urandom
from secret import flag
from binascii import unhexlify
from hashlib import sha256
from string import hexdigits
from signal import alarm

logo = '''
 _______   ________  ________       ___    ___ 
|\  ___ \ |\   __  \|\   ____\     |\  \  /  /|
\ \   __/|\ \  \|\  \ \  \___|_    \ \  \/  / /
 \ \  \_|/_\ \   __  \ \_____  \    \ \    / / 
  \ \  \_|\ \ \  \ \  \|____|\  \    \/  /  /  
   \ \_______\ \__\ \__\____\_\  \ __/  / /    
    \|_______|\|__|\|__|\_________\\\___/ /    
                       \|_________\|___|/

     ________  ________ ________         
    |\   ___ \|\  _____\\\   __  \        
    \ \  \_|\ \ \  \__/\ \  \|\  \       
     \ \  \ \\\ \ \   __\\\ \   __  \      
      \ \  \_\\\ \ \  \_| \ \  \ \  \     
       \ \_______\ \__\   \ \__\ \__\    
         \|_______|\|__|    \|__|\|__|    
                                                                                                                                 
'''


_memu = '''
1. Encrypt
2. Get flag
3. Exit
'''


def proof():
    plain = "".join([choice(hexdigits) for i in range(20)])
    print(plain)
    s = sha256(plain.encode()).hexdigest()
    print(f"sha256({plain[:16]}xxxx) = {s}")
    xxxx = input("plz enter the xxxx: ")
    if xxxx != plain[16:]:
        exit()


def rev(x):
    for i in range(32):
        x = rotl(x, 1)
    return x


def rotl(x, n): return ((x << n) & 0xffffffff) | ((x >> (32 - n)) & 0xffffffff)


def xorl(x, y): return list(map(lambda a, b: a ^ b, x, y))


def Int2List(x): return [x >> 24, (x >> 16) & 0xff, (x >> 8) & 0xff, x & 0xff]


def List2Int(x): return x[0] << 24 | x[1] << 16 | x[2] << 8 | x[3]


class Enc:
    def __init__(self, key):
        self.K = key
        self.S = sample([i for i in range(256)], 256)

    def l(self, B: list) -> list:
        B = List2Int(B)
        B = B ^ rotl(B, 2) ^ rotl(B, 10) ^ rotl(B, 18) ^ rotl(B, 24)
        return Int2List(B)

    def encrypt(self, plain):
        T = xorl(self.K[:4], plain)
        T = Int2List(rev(List2Int(T)))
        T = self.l([self.S[i] for i in T])
        T = xorl(self.K[4:], T)
        return bytes(T).hex()


def E():
    plain = input("plz enter your plaintext: ")
    print(f"cipher = {C.encrypt(unhexlify(plain))}")


def Get_Flag():
    print(f"cipher = {f}")
    plain = input("plz enter your plaintext: ")
    c = C.encrypt(unhexlify(plain))
    if c == f:
        print(flag)
        exit(0)
    else:
        print("wrong!")
        exit(0)


def memu():
    choose = input("> ")
    if choose == "1":
        E()
    elif choose == "2":
        Get_Flag()
    else:
        print("Bye~")
        exit(0)


if __name__ == "__main__":
    proof()
    print(logo)
    key = urandom(8)
    C = Enc(key)
    f = C.encrypt(urandom(4))
    print(f"sbox: {C.S}")
    print(_memu)
    alarm(10)
    while True:
        memu()

代码略有点长，一步一步来，还是从分析加密流程开始：

首先，要过一个proof，为爆破一个十六进制串的末四位哈希，这个本来没什么好讲的，但是仔细看可以发现题目这里锅了：

def proof():
    plain = "".join([choice(hexdigits) for i in range(20)])
    print(plain)
    s = sha256(plain.encode()).hexdigest()
    print(f"sha256({plain[:16]}xxxx) = {s}")
    xxxx = input("plz enter the xxxx: ")
    if xxxx != plain[16:]:
        exit()

可以看到，他直接print了明文串，因此只需要接受明文串，并把末四个十六进制数发送回去即可通过proof。其实这也没什么，不过是一个小失误。但之所以我要特地讲出来，在这篇wp后面会说明原因。

过了proof后，加密正式开始：

• 生成一个8字节的随机密钥key
• 用这个key初始化一个Enc对象C
• 生成一个4字节的随机明文，记作plain，并用Enc对象C进行加密，得到f
• 给出C中的S盒
• 给我们10s时间，可以选择进行以下两种操作：
• • 输入”1”，可以自行构造一组明文进行加密，靶机端会返回加密后的密文
  • 输入”2”，可以输入一个明文，如果输入的明文被加密后与f相等，则核验通过，发放flag

这是靶机端需完成的任务的逻辑，再来看看Enc对象具体是怎么加密的，也就是encrypt函数：

def encrypt(self, plain):
    T = xorl(self.K[:4], plain)
    T = Int2List(rev(List2Int(T)))
    T = self.l([self.S[i] for i in T])
    T = xorl(self.K[4:], T)
    return bytes(T).hex()

• 生成一个S盒，是一个(0,256)之间的随机置换
• 将明文与key的前四个字节作异或，得到T
• 第二行，做完了题也不知道有什么用，估计是出题没删干净
• 将T作S盒置换后，调用l函数，得到更新后的T
• 将T与key的后半段异或，并给出十六进制密文

其中，l函数如下：

def l(self, B: list) -> list:
    B = List2Int(B)
    B = B ^ rotl(B, 2) ^ rotl(B, 10) ^ rotl(B, 18) ^ rotl(B, 24)
    return Int2List(B)

你应该可以感觉到，如果能够知道l函数的密文，那么这种级别的加密对于z3来说，求解出明文不是难事。

至此，题目加密流程就梳理结束了，接下来进行到分析环节。

思路一：生日攻击

刚才我特意说，题目的proof锅了，不需要实际爆破，作用就在这里。节省下来的爆破时间给生日攻击提供了一点可能性。

你可以发现，题目实质上就是要求给出正确的4个明文字节。而4个字节一共有2^32次方种可能性，因此我们随便输入四个字节给靶机，也有 $ \frac{1}{2^{32}}$ 的机会成功。而失败了的话，就重新连接靶机，再随便输入四个字节，如此重复。根据生日攻击理论，如果能够反复进行2^32次，我们就有超过50%的几率至少成功攻击一次，那么就能拿到flag。

当然，即使proof锅了，真的要进行2^32次方次的话，可以用tqdm测试一下大概需要600000个小时，仍然是不现实的。但是这确实是个思路，一点办法都没有的时候，可以拼拼运气。

思路二：构造明文

生日攻击只能说有非常微小的成功的机会。真正要做的话，还是得分析一下加密流程，以及如何构造出可用的明文。

首先要注意到，我们只有10s时间，这是个非常重要的信息。经过我用tqdm测试，我们大概最多能构造30-40组明文让服务器加密。并且，考虑到还需要用构造出的明文信息对f进行解密，实际上来说可能最多只能构造10-20组明文。

这个用处挺大的，直接完全排除了中间相遇攻击、建立字典查找等思路。因此现在的主要目标就是：如何用有限的、少量的明文，去泄露Enc对象C的信息，从而解密密文。

你应该能看出来，如果你能获得密钥key的完整8个字节，那么解密是很容易的，只需要对应异或、逆置换、z3解方程就可以解密出明文。

因此，重心放在求解key上也就是自然而然的思路。很容易想到，如果发送四个字节的”\x00”给靶机端，那么再观察encrypt函数：

def encrypt(self, plain):
    T = xorl(self.K[:4], plain)
    T = Int2List(rev(List2Int(T)))
    T = self.l([self.S[i] for i in T])
    T = xorl(self.K[4:], T)
    return bytes(T).hex()

那么第一步得到的T其实就是key的前四个字节，在之后也是key的前四个字节进行置换、调用l函数等。

而第二次，考虑发送下面这样的字节串：

b"\x00" * 3 + b"\x01"

可以发现，第一部得到的T，前面三个字节并没有受到影响，仍然是key的前三个字节，只有最后一字节的最后一比特取了反。因此，到第三步置换时，前三个字节的置换仍然是不变的，变的只有第四个字节。也就是说，经过这两次明文的发送，l函数输入的参数列表只有最后一个发生了改变！

而我们再看l函数加密过程，为了直观我画个图像：

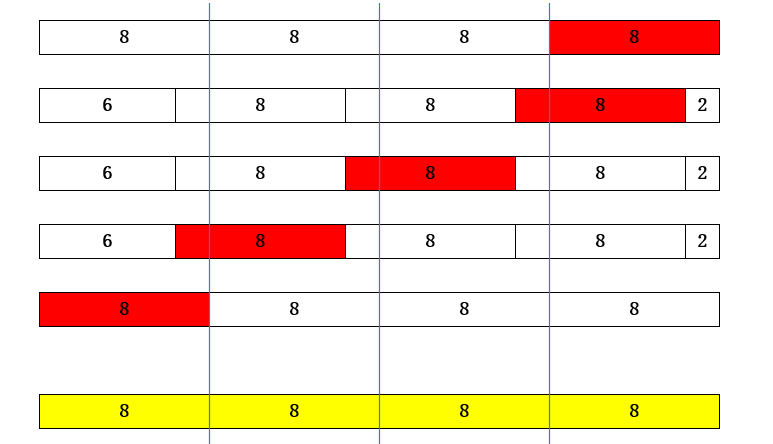
红色部分代表两次构造的明文在调l函数时的不同量，黄色部分代表得到密文，线条表示该线条与另一线条之间的五个部分异或得到下方的密文。

那么你仔细看这个图，你会发现，第二块密文和第三块密文，对于红色块异或的量是相同的！那么我们将两次服务器返回的密文异或，会发生什么呢？在下面的分析过程中，我们把key的前半部分记作key1，后半部分记作key2.

首先，我们把m经置换后的列表记作P(m)，经l函数后的列表记作l(P(m))，也就是m经第三步变换后，记作(l(P(m)))。那么两次构造明文到第三步前分别是key1、key1’，则有：

$$c1 \oplus c2 = (l(P(key_1)) \oplus key_2) \oplus (l(P(key_1')) \oplus key_2)$$

那么就可以消掉key2，即：

$$c1 \oplus c2 = l(P(key_1) \oplus l(P(key_1'))$$

而根据刚才的画图分析，密文中间两块对红色的异或利用是相同的，因此我们可以单独分析上式的中间两块，得到：

$$中间两块异或 = 两次明文的不同红色量异或$$

这一部分一定要结合图多理解理解，我没有想到讲的特别清楚的办法，如果哪里不明白可以与我交流。

而两次不同的红色量分别是(key1)和(key1^1)经置换得到的最后一字节，而我们拥有这个异或值以及S盒，因此可以反查到所有可能的解。一般来说会有1-4组。

那么通过上述方法，我们就获得了key1的一个字节，而类似的，通过构造下面几组明文并发送，可以通过相同的分析得到key1的剩下三个字节：

b"\x00"*2 + b"\x01"*1 +b"\x00"*1
b"\x00"*1 + b"\x01"*1 +b"\x00"*2
b"\x01"*1 + b"\x00"*3

而有了key1后，我们就可以发送key1作为明文，那么经第一步异或后得到的T就是四个全零字节，那么也就自然的可以得到第三步置换以及加密后的值，再与服务器返回的密文异或就能得到key2.

得到key2后，解密相对来说就很容易了，可以自行逆序实现。

需要注意的是，有一个地方导致我们可能不成功：

• 每次获得的key1的某字节可能有多解

但是没关系，我们只需要多与靶机交互几次，直到满足key1的四个字节都是正确解即可。这一段可以用下面的代码本地调试一下：

from random import sample, choice
from os import urandom
from binascii import *
from hashlib import sha256
from string import hexdigits
from Crypto.Util.number import *
from z3 import *

def rev(x):
    for i in range(32):
        x = rotl(x, 1)
    return x

def l(B):
    B = List2Int(B)
    B = B ^ rotl(B, 2) ^ rotl(B, 10) ^ rotl(B, 18) ^ rotl(B, 24)
    return Int2List(B)

def rotl(x, n): return ((x << n) & 0xffffffff) | ((x >> (32 - n)) & 0xffffffff)


def xorl(x, y): return list(map(lambda a, b: a ^ b, x, y))


def Int2List(x): return [x >> 24, (x >> 16) & 0xff, (x >> 8) & 0xff, x & 0xff]


def List2Int(x): return x[0] << 24 | x[1] << 16 | x[2] << 8 | x[3]

def decrypt(K,cipher):
    T = List2Int(xorl(K[4:],cipher))
    s = Solver() 
    B = BitVec('B',32)
    s.add(B ^ rotl(B, 2) ^ rotl(B, 10) ^ rotl(B, 18) ^ rotl(B, 24) == T)
    if s.check() == sat:    #检测是否有解
        result = str(s.model()) 
        T = Int2List(int(result[5:-1]))
        for i in range(len(T)):
            T[i] = inv_S[T[i]]
    T = List2Int(xorl(K[:4],T))
    return long_to_bytes(T).hex()


class Enc:
    def __init__(self, key):
        self.K = key
        self.S = sample([i for i in range(256)], 256)

    def l(self, B: list) -> list:
        B = List2Int(B)
        B = B ^ rotl(B, 2) ^ rotl(B, 10) ^ rotl(B, 18) ^ rotl(B, 24)
        return Int2List(B)

    def encrypt(self, plain):
        T = xorl(self.K[:4], plain)
        T = Int2List(rev(List2Int(T)))
        temp = [self.S[i] for i in T]
        T = self.l(temp)
        T = xorl(self.K[4:], T)
        return bytes(T)

def E(m):
    plain = hexlify(m)
    return C.encrypt(unhexlify(plain))

fin = 0
for kk in range(10):
    count = 0
    while(1):
        try:
            key = urandom(8)
            C = Enc(key)
            x = []
            x.append(E(b"\x00"*4))
            x.append(E(b"\x00"*3 + b"\x01"*1 +b"\x00"*0))
            x.append(E(b"\x00"*2 + b"\x01"*1 +b"\x00"*1))
            x.append(E(b"\x00"*1 + b"\x01"*1 +b"\x00"*2))
            x.append(E(b"\x00"*0 + b"\x01"*1 +b"\x00"*3))
            c = urandom(4)

            S = C.S
            inv_S = [0 for i in range(256)]
            for i in range(256):
                inv_S[S[i]] = i

            #获取key
            key_prefix = []

            #1.获取key[:4]
            for i in range(1,5):
                if(i % 2 == 0):
                    temp = (xorl(x[0],x[i]))[i-2]
                elif(i % 2 == 1):
                    temp = (xorl(x[0],x[i]))[i]
                for j in range(256):
                    t1 = (S[j]>>6) + ((S[j]&0b111111)<<2)
                    t2 = (S[j^1]>>6) + ((S[j^1]&0b111111)<<2)
                    if(t1^t2 == temp):
                        key_prefix.append(inv_S[S[j]])
                        break
            key_prefix = key_prefix[::-1]

            key_suffix = Int2List(bytes_to_long(E(long_to_bytes(List2Int(key_prefix)))))
            T = [0,0,0,0]
            temp = l([S[i] for i in T])
            key_suffix = xorl(temp, key_suffix)
            key_final = long_to_bytes(List2Int(key_prefix)) + long_to_bytes(List2Int(key_suffix))

            count += 1
            if(decrypt(key_final,E(c)) == c.hex()):
                break
        except:
            pass

    print(count)
    fin += count

print(fin//10)

可以计算出，平均需要180次左右，能获得一次key1的完全正确的解。运气好的话几组就能出，运气不好接近一千组也有可能，不过没事，交互挂着跑就好。

而本地能正确解密的话，我们就能顺利编写靶机代码了：

from Crypto.Util.number import *
from pwn import *
from binascii import *
from z3 import *

def rotl(x, n): return ((x << n) & 0xffffffff) | ((x >> (32 - n)) & 0xffffffff)

def xorl(x, y): return list(map(lambda a, b: a ^ b, x, y))

def List2Int(x): return x[0] << 24 | x[1] << 16 | x[2] << 8 | x[3]

def Int2List(x): return [x >> 24, (x >> 16) & 0xff, (x >> 8) & 0xff, x & 0xff]

def l(B):
    B = List2Int(B)
    B = B ^ rotl(B, 2) ^ rotl(B, 10) ^ rotl(B, 18) ^ rotl(B, 24)
    return Int2List(B)

def decrypt(K,cipher,inv_S):
    T = List2Int(xorl(K[4:],cipher))
    s = Solver() 
    B = BitVec('B',32)
    s.add(B ^ rotl(B, 2) ^ rotl(B, 10) ^ rotl(B, 18) ^ rotl(B, 24) == T)
    if s.check() == sat:    #检测是否有解
        result = str(s.model()) 
        T = Int2List(int(result[5:-1]))
        for i in range(len(T)):
            T[i] = inv_S[T[i]]
    T = List2Int(xorl(K[:4],T))
    return long_to_bytes(T).hex()

def getflag():
        while(1):
            try:
                r = remote("node4.anna.nssctf.cn",28579)
                temp = r.recvline().strip().decode()[-4:]
                r.sendline(temp.encode())
                r.recvuntil(b"sbox: ")
                S = eval(r.recvline())
                inv_S = [0 for i in range(256)]
                for i in range(256):
                    inv_S[S[i]] = i

                x = []
                #0
                temp = r.recvuntil(b"> ")
                r.sendline(b"1")
                temp = r.recvuntil(b" plaintext: ")
                r.sendline(hexlify(b"\x00"*4))
                temp = r.recvuntil(b"cipher =")
                x.append(unhexlify(r.recvline().strip()))

                #1
                temp = r.recvuntil(b"> ")
                r.sendline(b"1")
                temp = r.recvuntil(b" plaintext: ")
                r.sendline(hexlify(b"\x00"*3 + b"\x01"*1 +b"\x00"*0))
                temp = r.recvuntil(b"cipher =")		
                x.append(unhexlify(r.recvline().strip()))

                #2
                temp = r.recvuntil(b"> ")
                r.sendline(b"1")
                temp = r.recvuntil(b" plaintext: ")
                r.sendline(hexlify(b"\x00"*2 + b"\x01"*1 +b"\x00"*1))
                temp = r.recvuntil(b"cipher =")
                x.append(unhexlify(r.recvline().strip()))

                #3
                temp = r.recvuntil(b"> ")
                r.sendline(b"1")
                temp = r.recvuntil(b" plaintext: ")
                r.sendline(hexlify(b"\x00"*1 + b"\x01"*1 +b"\x00"*2))
                temp = r.recvuntil(b"cipher =")
                x.append(unhexlify(r.recvline().strip()))

                #4
                temp = r.recvuntil(b"> ")
                r.sendline(b"1")
                temp = r.recvuntil(b" plaintext: ")
                r.sendline(hexlify(b"\x00"*0 + b"\x01"*1 +b"\x00"*3))
                temp = r.recvuntil(b"cipher =")
                x.append(unhexlify(r.recvline().strip()))


                #获取key
                key_prefix = []

                #1.获取key[:4]
                for i in range(1,5):
                    if(i % 2 == 0):
                        temp = (xorl(x[0],x[i]))[i-2]
                    elif(i % 2 == 1):
                        temp = (xorl(x[0],x[i]))[i]
                    for j in range(255):
                        t1 = (S[j]>>6) + ((S[j]&0b111111)<<2)
                        t2 = (S[j^1]>>6) + ((S[j^1]&0b111111)<<2)
                        if(t1^t2 == temp):
                            key_prefix.append(inv_S[S[j]])
                            break
                key_prefix = key_prefix[::-1]

                #2.获取key[4:]
                temp = r.recvuntil(b"> ")
                r.sendline(b"1")
                temp = r.recvuntil(b" plaintext: ")
                r.sendline(hexlify(long_to_bytes(List2Int(key_prefix))))
                temp = r.recvuntil(b"cipher =")
                key_suffix = Int2List(bytes_to_long(unhexlify(r.recvline().strip())))
                T = [0,0,0,0]
                temp = l([S[i] for i in T])
                key_suffix = xorl(temp, key_suffix)
                key_final = long_to_bytes(List2Int(key_prefix)) + long_to_bytes(List2Int(key_suffix))


                #获取flag
                temp = r.recvuntil(b"> ")
                r.sendline(b"2")
                temp = r.recvuntil(b"cipher =")
                cipher = unhexlify(r.recvline().strip())
                t = decrypt(key_final,cipher,inv_S)
                r.sendline(t)
                temp = r.recvline()
                print(temp)
                if(b"wrong" not in temp):
                    return
                
                r.close()
            except:
                pass

getflag()

#NSSCTF{4f9d3982-be4b-4c4a-8ca0-db1a69b28b03}

就这一题而言，还是有不少不是很好讲清楚的地方，可能我的做法也并不简洁。如果看了这篇文章你有任何想说的，都欢迎与我交流！

newAES

题目来源：羊城杯 2023 决赛

题目：

#!/usr/bin/env python

SboxOriginal = (
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)

xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)


Rcon = (
    0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,
    0x80, 0x1B, 0x36, 0x6C, 0xD8, 0xAB, 0x4D, 0x9A,
    0x2F, 0x5E, 0xBC, 0x63, 0xC6, 0x97, 0x35, 0x6A,
    0xD4, 0xB3, 0x7D, 0xFA, 0xEF, 0xC5, 0x91, 0x39,
)


def text2matrix(text):
    text = int(text.hex(), 16)
    matrix = []
    for i in range(16):
        byte = (text >> (8 * (15 - i))) & 0xFF
        if i % 4 == 0:
            matrix.append([byte])
        else:
            matrix[i // 4].append(byte)
    return matrix


def matrix2text(matrix):
    text = 0
    for i in range(4):
        for j in range(4):
            text |= (matrix[i][j] << (120 - 8 * (4 * i + j)))
    return text.to_bytes(16, byteorder='big')


class AES:
    def __init__(self, master_key, Sbox=SboxOriginal):
        self.Sbox = Sbox
        self.InvSbox = [0]* 256
        for i in range(256):
            self.InvSbox[self.Sbox[i]] = i
        self.change_key(master_key)

    def change_key(self, master_key):
        self.round_keys = text2matrix(master_key)
        for i in range(4, 4 * 11):
            self.round_keys.append([])
            if i % 4 == 0:
                byte = self.round_keys[i - 4][0]        \
                     ^ self.Sbox[self.round_keys[i - 1][1]]  \
                     ^ Rcon[i // 4]
                self.round_keys[i].append(byte)

                for j in range(1, 4):
                    byte = self.round_keys[i - 4][j]    \
                         ^ self.Sbox[self.round_keys[i - 1][(j + 1) % 4]]
                    self.round_keys[i].append(byte)
            else:
                for j in range(4):
                    byte = self.round_keys[i - 4][j]    \
                         ^ self.round_keys[i - 1][j]
                    self.round_keys[i].append(byte)


    def encrypt(self, plaintext):
        self.plain_state = text2matrix(plaintext)

        self.__add_round_key(self.plain_state, self.round_keys[:4])

        for i in range(1, 10):
            self.__round_encrypt(self.plain_state, self.round_keys[4 * i : 4 * (i + 1)])

        self.__sub_bytes(self.plain_state)
        self.__shift_rows(self.plain_state)
        self.__add_round_key(self.plain_state, self.round_keys[40:])

        return matrix2text(self.plain_state)

    def decrypt(self, ciphertext):
        self.cipher_state = text2matrix(ciphertext)

        self.__add_round_key(self.cipher_state, self.round_keys[40:])
        self.__inv_shift_rows(self.cipher_state)
        self.__inv_sub_bytes(self.cipher_state)

        for i in range(9, 0, -1):
            self.__round_decrypt(self.cipher_state, self.round_keys[4 * i : 4 * (i + 1)])

        self.__add_round_key(self.cipher_state, self.round_keys[:4])

        return matrix2text(self.cipher_state)

    def __add_round_key(self, s, k):
        for i in range(4):
            for j in range(4):
                s[i][j] ^= k[i][j]


    def __round_encrypt(self, state_matrix, key_matrix):
        self.__sub_bytes(state_matrix)
        self.__shift_rows(state_matrix)
        self.__mix_columns(state_matrix)
        self.__add_round_key(state_matrix, key_matrix)


    def __round_decrypt(self, state_matrix, key_matrix):
        self.__add_round_key(state_matrix, key_matrix)
        self.__inv_mix_columns(state_matrix)
        self.__inv_shift_rows(state_matrix)
        self.__inv_sub_bytes(state_matrix)

    def __sub_bytes(self, s):
        for i in range(4):
            for j in range(4):
                s[i][j] = self.Sbox[s[i][j]]


    def __inv_sub_bytes(self, s):
        for i in range(4):
            for j in range(4):
                s[i][j] = self.InvSbox[s[i][j]]


    def __shift_rows(self, s):
        s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1]
        s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
        s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]


    def __inv_shift_rows(self, s):
        s[0][1], s[1][1], s[2][1], s[3][1] = s[3][1], s[0][1], s[1][1], s[2][1]
        s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
        s[0][3], s[1][3], s[2][3], s[3][3] = s[1][3], s[2][3], s[3][3], s[0][3]

    def __mix_single_column(self, a):
        t = a[0] ^ a[1] ^ a[2] ^ a[3]
        u = a[0]
        a[0] ^= t ^ xtime(a[0] ^ a[1])
        a[1] ^= t ^ xtime(a[1] ^ a[2])
        a[2] ^= t ^ xtime(a[2] ^ a[3])
        a[3] ^= t ^ xtime(a[3] ^ u)


    def __mix_columns(self, s):
        for i in range(4):
            self.__mix_single_column(s[i])


    def __inv_mix_columns(self, s):
        for i in range(4):
            u = xtime(xtime(s[i][0] ^ s[i][2]))
            v = xtime(xtime(s[i][1] ^ s[i][3]))
            s[i][0] ^= u
            s[i][1] ^= v
            s[i][2] ^= u
            s[i][3] ^= v

        self.__mix_columns(s)

import os
from secret import flag
from Crypto.Util.Padding import *


mybox = [105, 121, 73, 89, 41, 57, 9, 25, 233, 249, 201, 217, 169, 185, 137, 153, 104, 120, 72, 88, 40, 56, 8, 24, 232, 248, 200, 216, 168, 184, 136, 152, 107, 123, 75, 91, 43, 59, 11, 27, 235, 251, 203, 219, 171, 187, 139, 155, 106, 122, 74, 90, 42, 58, 10, 26, 234, 250, 202, 218, 170, 186, 138, 154, 109, 125, 77, 93, 45, 61, 13, 29, 237, 253, 205, 221, 173, 189, 141, 157, 108, 124, 76, 92, 44, 60, 12, 28, 236, 252, 204, 220, 172, 188, 140, 156, 111, 127, 79, 95, 47, 63, 15, 31, 239, 255, 207, 223, 175, 191, 143, 159, 110, 126, 78, 94, 46, 62, 14, 30, 238, 254, 206, 222, 174, 190, 142, 158, 97, 113, 65, 81, 33, 49, 1, 17, 225, 241, 193, 209, 161, 177, 129, 145, 96, 112, 64, 80, 32, 48, 0, 16, 224, 240, 192, 208, 160, 176, 128, 144, 99, 115, 67, 83, 35, 51, 3, 19, 227, 243, 195, 211, 163, 179, 131, 147, 98, 114, 66, 82, 34, 50, 2, 18, 226, 242, 194, 210, 162, 178, 130, 146, 101, 117, 69, 85, 37, 53, 5, 21, 229, 245, 197, 213, 165, 181, 133, 149, 100, 116, 68, 84, 36, 52, 4, 20, 228, 244, 196, 212, 164, 180, 132, 148, 103, 119, 71, 87, 39, 55, 7, 23, 231, 247, 199, 215, 167, 183, 135, 151, 102, 118, 70, 86, 38, 54, 6, 22, 230, 246, 198, 214, 166, 182, 134, 150]
plaintext = b"I will give you some hint: " + flag
plaintext = pad(plaintext,16,"pkcs7")
ciphertext = b"" 
key = os.urandom(16)
aes = AES(key, Sbox=mybox)
while len(plaintext) > 0:
    ciphertext += aes.encrypt(plaintext[:16])
    plaintext = plaintext[16:]
print(f'c = {ciphertext.hex()}')

# c = 26ec146dddda72b791585e5ecbc6a947bd6159d4de35df6c7717cd8eca1acd319f07803d8127f41b7ac7cdadc250ec8bb66f3661d772665a1622ffeba82996551463b738a997cd2c7081894fa9a5246c

题目代码不短，不过大部分是AES的具体实现，所以不用管。题目真正有用的信息其实就两点：

• 更换了一个AES的S盒
• 给了两组明文，以及AES加密后的对应密文

第一感觉应该是AES的某一部分作了小改动，然后导致产生了漏洞。但是把S盒换成普通的S盒之后，用自己构造的key，将明文分别用这个AES和cyberchef的AES进行加密，结果是完全一样的！说明这个AES真的就是完整、普通的AES加密，没有改动任何地方。

然后就懵了很久，因为好像没听说过AES还能已知明文攻击。但是题目目的其实已经很清楚了：根据这个更换的S盒以及两组明密文对，对AES进行已知明文攻击。

那肯定就是这个S盒设计的有问题，查阅后发现针对S盒确实有一种差分密码分析方式，然后就学习了一波：

密码分析（一）：差分密码分析-CSDN博客

简单说明一下我的理解，在这里我把差分分析的相关概念根据题目具体化一下：

差分：两组明文的异或值，就是明文差分；同理，两组密文的异或值，就是密文差分。

差分分析的依据：与密钥异或，不会改变差分

什么叫不会改变差分？我们把AES的行移位、列混淆都先不管，先单独看一下用到S盒的部分，也就是字节代换以及进行代换前的轮密钥加。这样的话，简单画个草图：

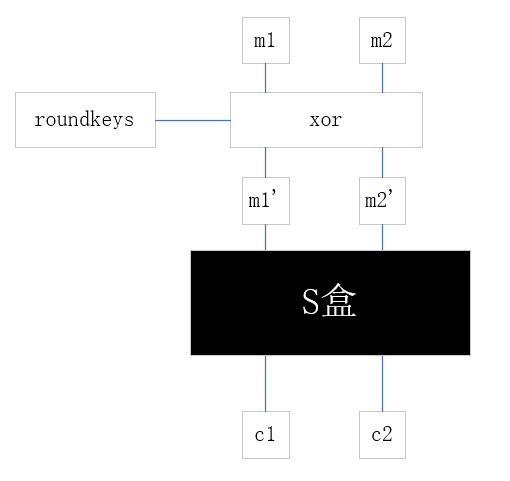
那么不会改变差分就体现在下面的式子中：若有

$$m_1 \oplus m_2 = t$$

则：

$$m_1' \oplus m_2' = (m_1\oplus roundkey) \oplus (m_2\oplus roundkey) = t$$

也就是说，轮密钥其实是对差分没有任何影响的，那么我们怎么利用这个事实进行攻击呢？

再回到刚才加密的那个图，可以看到，m1’经S盒代换后变成c1，m2’经S盒代换后变成c2，那么假设c1,c2的密文差分是r，那么我们就拥有了一个S盒的差分对 (t,r) 。

而S盒是一个字节代换操作，因此输入一共就有一个字节种可能，也就是256种，而对应的，所有可能的(m1,m2)明文对也就有256*256种，因此我们可以根据所有的(m1,m2)，用已知的S盒求出所有的(c1,c2)，从而求出所有明文差分及对应的密文差分，然后建立出一张S盒的差分表：

t = [[0 for i in range(256)] for j in range(256)]
for i in range(256):
    for j in range(256):
        t[i^j][sbox[i]^sbox[j]] += 1

那你应该要想到，这种差分对于一个设计良好的S盒来说，要显得很随机，因为S盒的字节代换本身是一个非线性操作，如果随机性不够，那么会让这个S盒有较大的概率暴露线性特征。

这么说可能还是有点抽象，直接列出两种S盒的差分表就直观了，简单打印一下前几行看看：

正常S盒的差分表：

[256, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 2, 0, 0, 2, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 0, 2, 2, 0, 0, 2, 2, 2, 0, 0, 0, 2, 4, 0, 2, 2, 0, 2, 0, 0, 0, 0, 2, 2, 0, 0, 2, 0, 2, 2, 2, 0, 0, 0, 2, 2, 2, 2, 2, 2, 2, 0, 0, 0, 2, 0, 0, 0, 2, 0, 0, 0, 2, 2, 0, 2, 2, 2, 0, 2, 2, 0, 2, 0, 2, 2, 0, 0, 0, 2, 2, 2, 0, 0, 0, 0, 0, 0, 0, 2, 2, 0, 2, 0, 0, 0, 2, 2, 2, 2, 0, 2, 0, 0, 0, 2, 0, 0, 2, 0, 0, 2, 2, 0, 0, 0, 2, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 0, 2, 2, 0, 0, 0, 2, 0, 0, 2, 0, 2, 0, 0, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 0, 2, 0, 2, 2, 2, 2, 2, 2, 0, 0, 2, 0, 2, 0, 2, 2, 2, 2, 0, 0, 2, 0, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 0, 2, 2, 0, 0, 0, 0, 2, 0, 0, 0, 2, 2, 0, 0, 2, 2, 0, 0, 2, 0, 0, 2, 0, 0, 2, 0, 0, 2, 2, 2, 0, 0, 2, 0, 0, 0, 2, 2, 2, 0, 2, 2, 0, 0, 0, 2]
[0, 0, 0, 2, 2, 2, 2, 2, 0, 0, 0, 2, 2, 2, 0, 2, 0, 2, 2, 0, 4, 0, 0, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0, 0, 0, 0, 2, 2, 0, 2, 0, 0, 2, 0, 2, 2, 2, 2, 0, 0, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0, 2, 0, 0, 0, 2, 2, 2, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 0, 2, 0, 2, 2, 0, 0, 0, 2, 0, 2, 2, 2, 0, 0, 0, 2, 2, 2, 0, 2, 0, 2, 0, 0, 2, 0, 0, 0, 2, 2, 2, 2, 2, 0, 0, 2, 0, 0, 2, 2, 2, 2, 2, 2, 0, 2, 0, 2, 0, 2, 0, 0, 2, 0, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 2, 2, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 0, 2, 0, 0, 2, 2, 0, 0, 0, 0, 0, 0, 0, 2, 0, 2, 2, 2, 0, 2, 2, 2, 2, 0, 2, 0, 0, 2, 0, 0, 2, 0, 2, 2, 2, 2, 2, 0, 0, 2, 2, 0, 0, 0, 0, 2, 2, 0, 0, 2, 0, 2, 0, 0, 2, 0, 0, 2, 2, 0, 2, 0, 0, 2, 0, 2, 0, 2, 0, 2, 2, 0, 0, 0, 2, 0, 0, 2, 0, 0, 2, 2, 2]
[0, 0, 2, 0, 2, 2, 0, 0, 2, 0, 2, 2, 2, 0, 0, 0, 0, 2, 2, 2, 2, 2, 2, 2, 4, 0, 0, 2, 0, 0, 2, 2, 0, 2, 2, 0, 2, 0, 0, 0, 2, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 2, 2, 0, 0, 2, 0, 0, 0, 0, 0, 2, 0, 0, 0, 2, 2, 2, 0, 2, 0, 0, 2, 0, 2, 2, 0, 0, 0, 2, 2, 0, 2, 2, 2, 0, 0, 0, 0, 2, 2, 0, 0, 2, 0, 2, 0, 2, 0, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 2, 2, 0, 0, 2, 2, 0, 0, 0, 0, 2, 2, 2, 2, 2, 0, 2, 2, 0, 0, 2, 2, 0, 2, 0, 2, 2, 0, 0, 0, 0, 0, 2, 2, 2, 2, 2, 0, 0, 0, 2, 0, 2, 0, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 0, 0, 2, 2, 0, 0, 2, 0, 2, 0, 0, 0, 0, 2, 0, 0, 2, 0, 0, 2, 2, 2, 0, 2, 0, 0, 2, 2, 0, 0, 2, 2, 2, 2, 0, 0, 0, 2, 0, 2, 0, 0, 2, 0, 2, 2, 0, 2, 2, 2, 2, 2, 0, 2, 0, 2, 0, 0, 2, 0, 2, 2, 2, 0, 0, 2, 2, 2, 0, 0, 2, 0, 2, 2, 0, 0, 0, 0, 2, 0, 2, 2, 2, 2, 2, 0, 2, 0, 2]

这个题目的S盒的差分表：

[256, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 256, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 256, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 256, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

能感受到区别了吧，这个题目的S盒的差分表完全就没有任何随机性，明文差分与密文差分完全是固定的！而这个固定的差分就不会受轮密钥加的影响，因此我们完全不需要密钥，把对应密钥的操作剔除掉即可。

也就是说，我们只需要将已知密文与未知密文求差分，然后将这个差分用AES解密(去除轮密钥加)，求出初始的明文差分，然后将这个差分与已知明文再求差分，就能得到未知的明文了。

需要注意的是，由于是对差分进行AES解密，所以用的并不是题目给的S盒，而是由S盒求出的差分S盒。

exp：

from Crypto.Util.number import *

def xor(a,b):
    return bytes([i^j for i,j in zip(a,b)])

xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)

Rcon = (
    0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,
    0x80, 0x1B, 0x36, 0x6C, 0xD8, 0xAB, 0x4D, 0x9A,
    0x2F, 0x5E, 0xBC, 0x63, 0xC6, 0x97, 0x35, 0x6A,
    0xD4, 0xB3, 0x7D, 0xFA, 0xEF, 0xC5, 0x91, 0x39,
)


def text2matrix(text):
    text = int(text.hex(), 16)
    matrix = []
    for i in range(16):
        byte = (text >> (8 * (15 - i))) & 0xFF
        if i % 4 == 0:
            matrix.append([byte])
        else:
            matrix[i // 4].append(byte)
    return matrix


def matrix2text(matrix):
    text = 0
    for i in range(4):
        for j in range(4):
            text |= (matrix[i][j] << (120 - 8 * (4 * i + j)))
    return text.to_bytes(16, byteorder='big')


class AES:
    def __init__(self, Sbox):
        self.Sbox = Sbox
        self.InvSbox = [0]* 256
        for i in range(256):
            self.InvSbox[self.Sbox[i]] = i

    def decrypt(self, ciphertext):
        self.cipher_state = text2matrix(ciphertext)
        self.__inv_shift_rows(self.cipher_state)
        self.__inv_sub_bytes(self.cipher_state)

        for i in range(9, 0, -1):
            self.__round_decrypt(self.cipher_state)

        return matrix2text(self.cipher_state)

    def __round_decrypt(self, state_matrix):
        self.__inv_mix_columns(state_matrix)
        self.__inv_shift_rows(state_matrix)
        self.__inv_sub_bytes(state_matrix)

    def __inv_sub_bytes(self, s):
        for i in range(4):
            for j in range(4):
                s[i][j] = self.InvSbox[s[i][j]]

    def __inv_shift_rows(self, s):
        s[0][1], s[1][1], s[2][1], s[3][1] = s[3][1], s[0][1], s[1][1], s[2][1]
        s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
        s[0][3], s[1][3], s[2][3], s[3][3] = s[1][3], s[2][3], s[3][3], s[0][3]

    def __mix_single_column(self, a):
        t = a[0] ^ a[1] ^ a[2] ^ a[3]
        u = a[0]
        a[0] ^= t ^ xtime(a[0] ^ a[1])
        a[1] ^= t ^ xtime(a[1] ^ a[2])
        a[2] ^= t ^ xtime(a[2] ^ a[3])
        a[3] ^= t ^ xtime(a[3] ^ u)


    def __mix_columns(self, s):
        for i in range(4):
            self.__mix_single_column(s[i])


    def __inv_mix_columns(self, s):
        for i in range(4):
            u = xtime(xtime(s[i][0] ^ s[i][2]))
            v = xtime(xtime(s[i][1] ^ s[i][3]))
            s[i][0] ^= u
            s[i][1] ^= v
            s[i][2] ^= u
            s[i][3] ^= v

        self.__mix_columns(s)

def get_sbox_diff(sbox):          
    t = [[0 for i in range(256)] for j in range(256)]
    for i in range(256):
        for j in range(256):
            t[i^j][sbox[i]^sbox[j]] += 1

    sbox_diff = [0 for i in range(256)]

    for i in range(256):
        for j in range(256):
            if t[i][j] == 256:
                sbox_diff[i] = j
    return sbox_diff

sbox = [105, 121, 73, 89, 41, 57, 9, 25, 233, 249, 201, 217, 169, 185, 137, 153, 104, 120, 72, 88, 40, 56, 8, 24, 232, 248, 200, 216, 168, 184, 136, 152, 107, 123, 75, 91, 43, 59, 11, 27, 235, 251, 203, 219, 171, 187, 139, 155, 106, 122, 74, 90, 42, 58, 10, 26, 234, 250, 202, 218, 170, 186, 138, 154, 109, 125, 77, 93, 45, 61, 13, 29, 237, 253, 205, 221, 173, 189, 141, 157, 108, 124, 76, 92, 44, 60, 12, 28, 236, 252, 204, 220, 172, 188, 140, 156, 111, 127, 79, 95, 47, 63, 15, 31, 239, 255, 207, 223, 175, 191, 143, 159, 110, 126, 78, 94, 46, 62, 14, 30, 238, 254, 206, 222, 174, 190, 142, 158, 97, 113, 65, 81, 33, 49, 1, 17, 225, 241, 193, 209, 161, 177, 129, 145, 96, 112, 64, 80, 32, 48, 0, 16, 224, 240, 192, 208, 160, 176, 128, 144, 99, 115, 67, 83, 35, 51, 3, 19, 227, 243, 195, 211, 163, 179, 131, 147, 98, 114, 66, 82, 34, 50, 2, 18, 226, 242, 194, 210, 162, 178, 130, 146, 101, 117, 69, 85, 37, 53, 5, 21, 229, 245, 197, 213, 165, 181, 133, 149, 100, 116, 68, 84, 36, 52, 4, 20, 228, 244, 196, 212, 164, 180, 132, 148, 103, 119, 71, 87, 39, 55, 7, 23, 231, 247, 199, 215, 167, 183, 135, 151, 102, 118, 70, 86, 38, 54, 6, 22, 230, 246, 198, 214, 166, 182, 134, 150]
m = b"I will give you some hint: DASCT"
ciphertext = b"" 
aes = AES(Sbox=get_sbox_diff(sbox))

c = "26ec146dddda72b791585e5ecbc6a947bd6159d4de35df6c7717cd8eca1acd319f07803d8127f41b7ac7cdadc250ec8bb66f3661d772665a1622ffeba82996551463b738a997cd2c7081894fa9a5246c"
c1 = long_to_bytes(int(c[:64],16))
c2 = long_to_bytes(int(c[64:],16))
print("DASCT",end = "")
for i in range(len(c2)//16):
    diff1 = xor(c1[:16],c2[16*i:16*i+16])
    temp1 = aes.decrypt(diff1)
    print(str(xor(temp1,m[:16]))[2:-1],end = "")

#DASCTF{de423c9aa5df7e683bd4b08bbca2a3409c018867}

aes

题目来源：EIS 2019

题目：

#!/usr/bin/env python3
# coding=utf-8

import os
import signal
from Crypto.Cipher import AES
from Crypto.Util import Counter

def enc(msg, key):
    ctr = Counter.new(128,  initial_value=sum(msg))
    cipher = AES.new(key, AES.MODE_CTR, counter=ctr)
    return cipher.encrypt(msg)

if __name__ == '__main__':
    signal.alarm(60)
    key = os.urandom(16)
    with open('/home/ctf/flag', 'rb') as f:
        flag = f.read()
    assert len(flag) == 30
    enc_flag = enc(flag, key)

    print("Welcome to the our AES encryption system!")
    print(f"Here is your encrypted flag: {enc_flag}")
    for i in range(30):
        try:
            plaintext = input("Please input your plaintext: ")
            plaintext = bytes.fromhex(plaintext)
            ciphertext = enc(plaintext, key)
            print(f"Here is your ciphertext: {ciphertext}")
        except Exception:
            print('Error!')
            break
    print('Bye~')

靶机提供了如下操作：

• 连接上靶机后，开始计时60s
• 随机生成十六字节作为AES密钥
• 使用AES_CTR模式对flag进行加密，其中Counter由flag的所有字节和生成，并给出flag的加密值
• 可以与服务器进行三十次交互，每一次交互中，可以输入一段明文，并获得其AES_CTR模式的加密值，对应Counter仍然由输入明文的字节和产生

首先就注意到用了一个平时不怎么见的AES_CTR模式，那么问题肯定也出在这里，先了解一波CTR模式是什么：

AES的CTR模式加密解密详解 | Wuman’s Blog (wumansgy.github.io)

其核心如下：

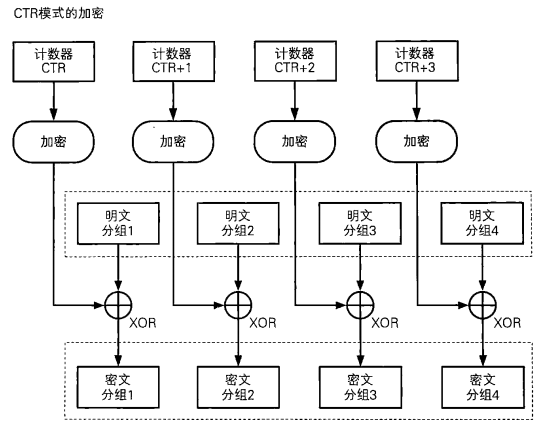
可以看到，他的AES加密是作用于Counter而非明文。也就是说，其加密流程是将被AES加密的Counter与明文异或得到密文。

而这道题显然提供了Counter的额外信息，也就是其initial_value是传入明文的字节和。而flag固定为30个字节，因此其和只有256*30种可能性，完全可以爆破。而当我们取的明文值字节和正好等于flag的字节和时，其AES加密的结果相同，因此有：

flag = flag_enc ^ input ^ input_enc

至于限时60s以及限30次，完全不重要，因为可以反复连接靶机而flag不会变。当然注意输入明文长度应与flag一致，均为30。

然而，在NSS上复现本题时，爆破完所有范围依然没有结果，此时打印出传回的flag_enc，发现是45字节，说明题目改动了flag与容器镜像的附件，但是下发的附件忘记改了，因此需要扩大范围至256*45。并且由于改动过flag，那么flag头应该考虑”NSSCTF”。同时，考虑到flag均为可见字符，因此复现时还可以进一步缩小一点范围。

exp：

from Crypto.Util.number import *
from pwn import *
from tqdm import *

#context.log_level = 'debug'

for count in trange(256//2*3):
    r = remote("node4.anna.nssctf.cn",28353)
    r.recvuntil(b"flag:")
    flag_enc = eval(r.recvline().strip().decode())

    for i in range(30):
        r.recvuntil(b"plaintext: ")
        num = 30 * count + i
        input1 = b""
        while(num > 255):
            num -= 255
            input1 += b"\xff"
        input1 += long_to_bytes(num)
        pad = (45-len(input1))*b"\x00"
        input1 += pad           
        r.sendline(input1.hex())
        r.recvuntil(b"ciphertext:")
        input_c = eval(r.recvline().strip().decode())
        flag = long_to_bytes(bytes_to_long(input_c) ^ bytes_to_long(flag_enc) ^ bytes_to_long(input1))
        if(b"NSSCTF" in flag):
            print(flag)
            exit()
    r.close()

#NSSCTF{b93abc9b-7972-4c46-b13f-5eed06787edc}

3DES

题目来源：暂不明确

题目：

import os
from secret import flag
from Crypto.Cipher import DES
from Crypto.Util.Padding import pad
from Crypto.Util.strxor import strxor

def expand(k):
    k=k.hex()
    k=''.join('0'+c for c in k)
    k=bytes.fromhex(k)
    return k

k1=expand(os.urandom(4))
k2=expand(os.urandom(4))
k3=expand(os.urandom(4))

msg=pad(b'The flag:'+flag,8)
enc1=DES.new(k1,mode=DES.MODE_ECB).encrypt(msg)
enc2=strxor(enc1,k2*(len(msg)//len(k2)))
enc3=DES.new(k3,mode=DES.MODE_ECB).encrypt(enc2)
print(enc3.hex())
#e31e0ba78a911e14e8a2ae20fc7410e5d615d6841671497ee576749128a6df8b442912d910e82bd3ee463adaeebf91321060225d1308c20c4044af1add539b48b80bce411aad4a24fba68a89b2bfd3c1ee7cdae49b48acfd

题目先生成三个4字节的key，并按如下方式将他们扩展到八字节：

• 转为十六进制
• 在每个十六进制字符前面加一个0
• 转为字节流

举个例子，如果生成的四字节key是：

b"1111"

其十六进制为：

"31313131"

那么最终expand后得到的八字节就是：

b'\x03\x01\x03\x01\x03\x01\x03\x01'

讲完这个过程后回头看题目，他将三个key分别用在：

• 第一层的DES加密
• 第二层的异或加密
• 第三层的DES加密

然后给出了9个字节的已知明文头以及密文，要求解出明文。

由于DES加密分组为8字节一组，所以现在我们相当于拥有一组已知的明密文对，而看到这几层加密不难想到是要中间相遇攻击。具体来说，中间相遇的思路是：

• 爆破k1去加密已知明文分组，建立字典
• 爆破k3去解密对应密文分组，查字典
• 如果在字典中，则是可能的k1、k3，可以进行解密来看是否有可见flag来判断是否是正确的密钥对

但是这样没有考虑到k2的影响，事实上由于k2的存在，是没有办法直接用k1的加密值去建立字典的。不过，注意到k2也expand了，所以其对应十六进制的奇数位置的字符都是0，所以这些位置的k1加密值等于没有异或，因此只需要把这些位置的字符存入字典即可。

这样解决了怎么去中间相遇的问题，下一个问题就是复杂度。由于k1、k3都是随机4字节，那么要爆破的话，首先时间复杂度就是2^32往上，并且建立的字典也有2^32项，还要存关键字以及值，所以内存怎么也得用几十G，还得换机器跑。虽然说如果用C++写以及合适的机器跑的话似乎也勉强可以接受，但是还是太臃肿了。

然后突然反应过来这是DES，而DES的密钥看似是64bit，实际上是56bit，因为每个字节的最后一位本来是用于奇偶校验的，并不参与加密解密。因此回看expand后的key就可以少爆8bit，这样一下子就大大减小了时间和空间的压力，几分钟就可以跑出来。

exp：

from Crypto.Cipher import DES
from tqdm import *
from Crypto.Util.number import *
from itertools import product
from Crypto.Util.strxor import strxor
from Crypto.Util.Padding import unpad

#part1 construct dic
msg = b'The flag'
dic = {}
for i in tqdm(product(range(8),repeat = 8)):
    tt1 = [hex(2*j)[2:] for j in list(i)]
    temp=''.join('0'+c for c in tt1)
    k1 = bytes.fromhex(temp)
    enc1 = DES.new(k1,mode=DES.MODE_ECB).encrypt(msg)
    enc1 = enc1.hex()
    tt = enc1[0] + enc1[2] + enc1[4] + enc1[6] + enc1[8] + enc1[10] + enc1[12] + enc1[14]
    dic[tt] = tt1


#part2 mitm and get flag
c_prefix = long_to_bytes(int("e31e0ba78a911e14",16))
c = long_to_bytes(int("e31e0ba78a911e14e8a2ae20fc7410e5d615d6841671497ee576749128a6df8b442912d910e82bd3ee463adaeebf91321060225d1308c20c4044af1add539b48b80bce411aad4a24fba68a89b2bfd3c1ee7cdae49b48acfd",16))
for i in tqdm(product(range(8),repeat = 8)):
    tt1 = [hex(2*j)[2:] for j in list(i)]
    temp=''.join('0'+k for k in tt1)
    k3 = bytes.fromhex(temp)
    dec2 = DES.new(k3,mode=DES.MODE_ECB).decrypt(c_prefix)
    dec2 = dec2.hex()
    tt = dec2[0] + dec2[2] + dec2[4] + dec2[6] + dec2[8] + dec2[10] + dec2[12] + dec2[14]
    if(tt in dic):
        k1 = dic[tt]
        k1 = bytes.fromhex(''.join('0'+k for k in k1))

        #get k2
        enc1 = DES.new(k1,mode=DES.MODE_ECB).encrypt(msg)
        dec2 = DES.new(k3,mode=DES.MODE_ECB).decrypt(c_prefix)
        k2 = strxor(enc1,dec2[:8])

        #try to decrypt
        dec2 = DES.new(k3,mode=DES.MODE_ECB).decrypt(c)
        dec1 = strxor(dec2,k2*(len(c)//len(k2)))
        flag = DES.new(k1,mode=DES.MODE_ECB).decrypt(dec1)

        try:
            flag = unpad(flag,8).decode()
            print(flag)
        except:
            pass


#DASCTF{b3ffef61aaa0d088baf2c53abd8cccbf21b8bcd697a335f46ccc6b542f5437e9}