糖醋小鸡块的blog
0%

Crypto趣题-其他

发表于 更新于 分类于 Valine：

该文章主要记录一些特殊的趣题

Shamir门限

题目来源：暂不明确

题目：

1
2
3
4
5
6
7
8
9
公司使用Shamir门限密钥设计了一个秘密保存方案，将fag保存了起来，最终的设计效果如下密钥总共有9份，拿到任意5个密钥即可解出保存的flag.现在我们知道公共的密钥:
p=0x3b9f64aeadae9545d899102c8c1874e3d4f12caf6ded3eb8454c27fd7058ff31a5742aee60b2b7
以及如下5个密钥:
0x13570e530aaa3639e622d02ca8a0f89089ad0ee3ba51edd95490653b684aaeedd3a762938d08b3
0xb583b75e84190f9d081234088b23e6b634110bda167a21bdfb4b5608a65e7283e8531547623d8
0x8d3bbbb28592b1a00885c11633369568fcb8bbfdec3cbf4d8cd5546728ca99f24cbe0ac214a39
0x13816f03e972210516c17b13a008ee8fd9b888839d6e1ce203fd7723f5e8e0443c2c6279c8dab9
0x1553e323763e4c3ba53f6f93e0feb01d6b168fdda30fd87e949664eb4c8f2fd8414e2c14df8f5e
请恢复flag

题目明确说了这是一个Shamir门限方案，先来简单梳理一下Shamir门限方案的基本实施方式，大概分为以下几步:

1、根据恢复秘密最小人数及秘密消息，生成秘密多项式

  • 将秘密消息转化为整数，记为 secret
  • 首先，设置一个需恢复秘密的最小人数 t ，而题目中说”拿到任意5个密钥即可解出保存的flag”，因此t=5
  • 设置一个公钥 p ，作为之后生成的多项式所处的有限域
  • 生成一个 t-1 次的多项式，满足：
  • 因此可以看出，当多项式取 x=0 时，对应的 f(x)=f(0)=a0=secret，即秘密消息


2、根据秘密多项式，进行密钥分发

  • 设实际参与密钥分发的人数为 n ，则将 1~n(有时也可能是n个不同的随机数)依次代入秘密多项式 f(x)，便得到n组密钥：
  • 将生成的 n 个密钥分发给 n 个人


3、销毁秘密多项式


至此，Shamir门限方案便实施完成了，这种分法方案涉及到两个数字，一个是需恢复秘密的最小人数 t ，一个是实际参与密钥分发的人数 n ，因此可以称为 (t,n) - 门限方案。

需要注意到的是，在完成密钥分发之后，秘密多项式便随之被销毁了。那么在拥有足够数量的密钥(>=t)的情况下，怎么恢复秘密信息 secret呢？这就需要用到拉格朗日插值公式，我们不妨先把密钥记为:

则插值多项式如下：

直观一点可以展开写成下式：

观察一下这个多项式的性质：

  • 是一个 t-1 次多项式
  • 分发的密钥均是多项式上的点：
  • 这是因为，代入其中任意一个密钥的横坐标，则只有代入的那一项不为0，而其他全为0，拿 x1 举例：
  • 即：

所以当有足够多的点( t-1 次多项式需要 t 个点)进行插值时，就可以代入 0 进入插值多项式，解出的常数项即为秘密消息 secret


完全了解了Shamir门限方案后再来看这个题，就可以发现密钥数量是完全足够的，但是不清楚5个人具体分到的是9个密钥中的哪一个密钥，因此还需要全排列爆破处理。

exp.py：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from itertools import permutations
from Crypto.Util.number import *

p = 0x3b9f64aeadae9545d899102c8c1874e3d4f12caf6ded3eb8454c27fd7058ff31a5742aee60b2b7
c = [0x13570e530aaa3639e622d02ca8a0f89089ad0ee3ba51edd95490653b684aaeedd3a762938d08b3,0xb583b75e84190f9d081234088b23e6b634110bda167a21bdfb4b5608a65e7283e8531547623d8,0x8d3bbbb28592b1a00885c11633369568fcb8bbfdec3cbf4d8cd5546728ca99f24cbe0ac214a39,0x13816f03e972210516c17b13a008ee8fd9b888839d6e1ce203fd7723f5e8e0443c2c6279c8dab9,0x1553e323763e4c3ba53f6f93e0feb01d6b168fdda30fd87e949664eb4c8f2fd8414e2c14df8f5e]

m = ([0, c[0]],[0, c[1]],[0, c[2]],[0, c[3]],[0, c[4]])
for i in permutations(range(9),5):
        m[0][0] = i[0]
        m[1][0] = i[1]
        m[2][0] = i[2]
        m[3][0] = i[3]
        m[4][0] = i[4]
        try:
            r = (
                m[0][1] * (0 - m[1][0]) * (0 - m[2][0]) * (0 - m[3][0]) * (0 - m[4][0]) * inverse((m[0][0] - m[1][0]) * (m[0][0] - m[2][0]) * (m[0][0] - m[3][0]) * (m[0][0] - m[4][0]), p) +
                m[1][1] * (0 - m[0][0]) * (0 - m[2][0]) * (0 - m[3][0]) * (0 - m[4][0]) * inverse((m[1][0] - m[0][0]) * (m[1][0] - m[2][0]) * (m[1][0] - m[3][0]) * (m[1][0] - m[4][0]), p) +
                m[2][1] * (0 - m[1][0]) * (0 - m[0][0]) * (0 - m[3][0]) * (0 - m[4][0]) * inverse((m[2][0] - m[1][0]) * (m[2][0] - m[0][0]) * (m[2][0] - m[3][0]) * (m[2][0] - m[4][0]), p) +
                m[3][1] * (0 - m[1][0]) * (0 - m[2][0]) * (0 - m[0][0]) * (0 - m[4][0]) * inverse((m[3][0] - m[1][0]) * (m[3][0] - m[2][0]) * (m[3][0] - m[0][0]) * (m[3][0] - m[4][0]), p) +
                m[4][1] * (0 - m[1][0]) * (0 - m[2][0]) * (0 - m[3][0]) * (0 - m[0][0]) * inverse((m[4][0] - m[1][0]) * (m[4][0] - m[2][0]) * (m[4][0] - m[3][0]) * (m[4][0] - m[0][0]), p)
                ) % p
            temp = str(long_to_bytes(r))
            if("flag" in temp):
                print(temp)
        except:
            pass
        
#flag{b14f4963671a457cf22ec271356e0f78}



sqrt

题目来源：bricsctf-2023-Quals

题目：

1
2
3
4
5
from sage.all import *
import hashlib
P = Permutations(256).random_element()
print(P**2)
print([x^y for x,y in zip(hashlib.sha512(str(P).encode()).digest(), open('flag.txt', 'rb').read())])

密文txt：

1
2
[41, 124, 256, 27, 201, 93, 40, 133, 47, 10, 69, 253, 13, 245, 165, 166, 118, 230, 197, 249, 115, 18, 71, 24, 100, 14, 160, 28, 251, 96, 106, 5, 244, 58, 67, 44, 150, 42, 255, 74, 168, 182, 153, 209, 227, 232, 159, 128, 125, 11, 135, 90, 76, 30, 84, 31, 1, 149, 48, 95, 216, 94, 157, 131, 196, 172, 105, 169, 202, 203, 121, 210, 53, 9, 147, 89, 39, 68, 59, 141, 87, 207, 51, 180, 19, 81, 57, 103, 228, 77, 12, 129, 185, 85, 45, 123, 50, 116, 65, 213, 104, 64, 54, 155, 222, 112, 3, 252, 21, 33, 138, 151, 211, 233, 204, 97, 239, 113, 82, 200, 23, 231, 177, 26, 72, 4, 78, 183, 199, 6, 49, 29, 250, 119, 32, 56, 110, 187, 35, 143, 83, 25, 70, 2, 66, 101, 217, 120, 224, 142, 191, 136, 189, 127, 132, 36, 174, 146, 152, 140, 193, 62, 178, 17, 148, 248, 167, 88, 73, 229, 134, 156, 158, 60, 63, 242, 221, 34, 214, 20, 171, 139, 226, 186, 164, 181, 236, 107, 111, 61, 99, 108, 179, 223, 137, 212, 237, 102, 161, 145, 184, 173, 247, 162, 205, 154, 55, 117, 254, 38, 75, 234, 7, 46, 109, 22, 175, 144, 219, 220, 195, 190, 98, 79, 15, 170, 80, 235, 52, 8, 37, 243, 198, 86, 43, 192, 241, 240, 208, 130, 188, 114, 218, 215, 206, 176, 238, 16, 246, 126, 122, 163, 225, 92, 91, 194]
[18, 188, 48, 47, 100, 234, 225, 8, 187, 34, 124, 113, 118, 252, 137, 196, 125, 20, 251, 168, 167, 5, 225, 134, 66, 203, 26, 148, 63, 181, 213, 124, 170, 234, 35, 120, 47, 69, 157, 69, 194]

题目非常简短，流程如下：

  • 将256个元素进行全排列，并随机抽取其中一个排列，记为 P
  • 打印出该排列的平方
  • 将该排列 P 的 sha512 值与flag明文相异或，打印出密文

因此，任务就只有一个：根据排列的平方，还原出该排列，并与密文异或就能还原flag

有一个概念一定要先理解清楚，排列的平方是什么意思？用代码可以如下表示：

1
C[i] = P[P[i]]

也就是说，一组排列可以看作是一个置换，那么排列的平方就是进行二重置换。

那么怎么还原呢，我们用图的方式来理解，图上一个节点指向另一个节点，代表的就是经过一次置换后，该节点置换到指向节点的位置，比如下面这张图就可以表示一个置换：

(偶数个点的情况)

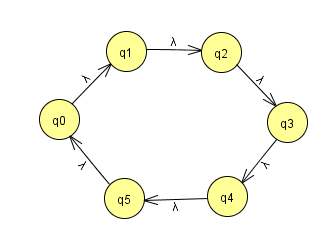
image-20230926104953693

这张图代表：0置换到1、1置换到2、…5置换到0，这很好理解

那么这个置换平方后会是什么样子？很简单，只需要把一个节点指向节点所指向的节点作为新的置换即可，说起来有点绕，还是举个例子：0指向1，1指向2，所以平方后，0指向2，这就很容易明白了。

所以上面的置换平方后会变成如下形式：

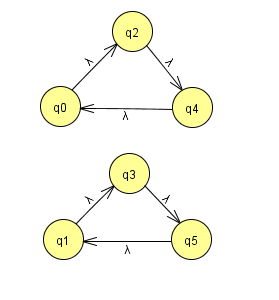
image-20230926105347447

那么还原的方式就是将两个环并排，然后挨个插入，如下：

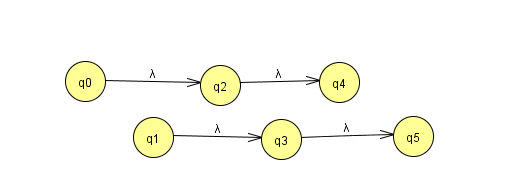
image-20230926105546460

但是显然，由于插入的相对位置不同，这样还原就可能会得到多个不同的初始置换，而他们平方后都是满足要求的。

上面的例子是偶数个点的情况，想一想奇数个点平方后会如何：

(奇数个点的情况)

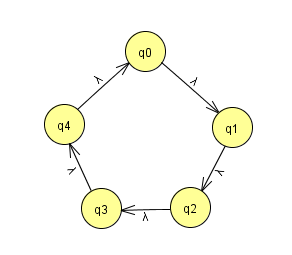
image-20230926105945860

继续利用把一个节点指向节点所指向的节点作为新的置换这一点，可以看出平方后，环并没有裂开，只是交换了位置：

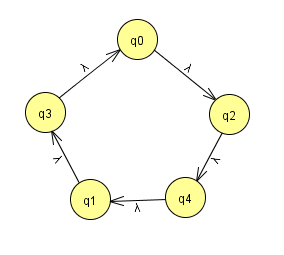
image-20230926110200084

仔细想想就能明白，这种形式的还原是唯一的，不会有多种情况。

想清楚置换与图的关系后，回到题目本身来，按如下步骤分析：

1、首先就要把平方后的排列先转化为若干个环：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#打印环
n = [18, 188, 48, 47, 100, 234, 225, 8, 187, 34, 124, 113, 118, 252, 137, 196, 125, 20, 251, 168, 167, 5, 225, 134, 66, 203, 26, 148, 63, 181, 213, 124, 170, 234, 35, 120, 47, 69, 157, 69, 194]

P2 = [41, 124, 256, 27, 201, 93, 40, 133, 47, 10, 69, 253, 13, 245, 165, 166, 118, 230, 197, 249, 115, 18, 71, 24, 100, 14, 160, 28, 251, 96, 106, 5, 244, 58, 67, 44, 150, 42, 255, 74, 168, 182, 153, 209, 227, 232, 159, 128, 125, 11, 135, 90, 76, 30, 84, 31, 1, 149, 48, 95, 216, 94, 157, 131, 196, 172, 105, 169, 202, 203, 121, 210, 53, 9, 147, 89, 39, 68, 59, 141, 87, 207, 51, 180, 19, 81, 57, 103, 228, 77, 12, 129, 185, 85, 45, 123, 50, 116, 65, 213, 104, 64, 54, 155, 222, 112, 3, 252, 21, 33, 138, 151, 211, 233, 204, 97, 239, 113, 82, 200, 23, 231, 177, 26, 72, 4, 78, 183, 199, 6, 49, 29, 250, 119, 32, 56, 110, 187, 35, 143, 83, 25, 70, 2, 66, 101, 217, 120, 224, 142, 191, 136, 189, 127, 132, 36, 174, 146, 152, 140, 193, 62, 178, 17, 148, 248, 167, 88, 73, 229, 134, 156, 158, 60, 63, 242, 221, 34, 214, 20, 171, 139, 226, 186, 164, 181, 236, 107, 111, 61, 99, 108, 179, 223, 137, 212, 237, 102, 161, 145, 184, 173, 247, 162, 205, 154, 55, 117, 254, 38, 75, 234, 7, 46, 109, 22, 175, 144, 219, 220, 195, 190, 98, 79, 15, 170, 80, 235, 52, 8, 37, 243, 198, 86, 43, 192, 241, 240, 208, 130, 188, 114, 218, 215, 206, 176, 238, 16, 246, 126, 122, 163, 225, 92, 91, 194]
for i in range(len(P2)):
    P2[i] -= 1
print(P2[204])
lenlist = []
for i in range(len(P2)):
    len = 1
    t = 0
    loc = P2[i]
    chain = [loc]
    while(1):
        t = P2[loc]
        loc = t
        chain.append(loc)
        len += 1
        if(t == i):
            #print(i,",",len)
            if(len == 2):
                print(chain)
                print(i+1)
            break
#print(lenlist.count(2))
#2*82 + 75 + 3*3 + 1*8

可以发现，平方后的置换可以拆分为 ：

  • 2个长为 82 的环
  • 1个长为75的环
  • 3个长为3的环
  • 8个单元环


2、接下来就是分析如何还原：

  • 对于长为 82 的环，他一定是长为 164 的环拆分而成
  • 长为 75 的环一定是本身长就为 75 的环
  • 3个长为3的环，可能本身就是 3 个长为 3 的环；也可能本身是一个长为 3 的环加上一个长为 6 的环拆分而成
  • 8个单元环，可能本身就是 8 个单元环，也可能是 1-4 个 2 元环加上剩下的单元环

因此，要考虑上述的所有可能情况，求出所有符合要求的排列，并与密文异或做爆破。按理来说，一般爆破需要的是flag头，但是由于我并不知道flag头是什么(别的师傅问的)，所以采用全为可见字符来爆破。

复杂度经计算应该是 ：(对哪一部分复杂度不清楚可以问我) 

1
82*1*4*C(8,2)*C(6,2)*C(4,2)*16

约为一千多万，大概跑五分钟左右可以全部完成。

exp.py：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
from Crypto.Util.number import *
import hashlib
from itertools import combinations

#打印环
'''
n = [18, 188, 48, 47, 100, 234, 225, 8, 187, 34, 124, 113, 118, 252, 137, 196, 125, 20, 251, 168, 167, 5, 225, 134, 66, 203, 26, 148, 63, 181, 213, 124, 170, 234, 35, 120, 47, 69, 157, 69, 194]

P2 = [41, 124, 256, 27, 201, 93, 40, 133, 47, 10, 69, 253, 13, 245, 165, 166, 118, 230, 197, 249, 115, 18, 71, 24, 100, 14, 160, 28, 251, 96, 106, 5, 244, 58, 67, 44, 150, 42, 255, 74, 168, 182, 153, 209, 227, 232, 159, 128, 125, 11, 135, 90, 76, 30, 84, 31, 1, 149, 48, 95, 216, 94, 157, 131, 196, 172, 105, 169, 202, 203, 121, 210, 53, 9, 147, 89, 39, 68, 59, 141, 87, 207, 51, 180, 19, 81, 57, 103, 228, 77, 12, 129, 185, 85, 45, 123, 50, 116, 65, 213, 104, 64, 54, 155, 222, 112, 3, 252, 21, 33, 138, 151, 211, 233, 204, 97, 239, 113, 82, 200, 23, 231, 177, 26, 72, 4, 78, 183, 199, 6, 49, 29, 250, 119, 32, 56, 110, 187, 35, 143, 83, 25, 70, 2, 66, 101, 217, 120, 224, 142, 191, 136, 189, 127, 132, 36, 174, 146, 152, 140, 193, 62, 178, 17, 148, 248, 167, 88, 73, 229, 134, 156, 158, 60, 63, 242, 221, 34, 214, 20, 171, 139, 226, 186, 164, 181, 236, 107, 111, 61, 99, 108, 179, 223, 137, 212, 237, 102, 161, 145, 184, 173, 247, 162, 205, 154, 55, 117, 254, 38, 75, 234, 7, 46, 109, 22, 175, 144, 219, 220, 195, 190, 98, 79, 15, 170, 80, 235, 52, 8, 37, 243, 198, 86, 43, 192, 241, 240, 208, 130, 188, 114, 218, 215, 206, 176, 238, 16, 246, 126, 122, 163, 225, 92, 91, 194]
for i in range(len(P2)):
    P2[i] -= 1
print(P2[204])
lenlist = []
for i in range(len(P2)):
    len = 1
    t = 0
    loc = P2[i]
    chain = [loc]
    while(1):
        t = P2[loc]
        loc = t
        chain.append(loc)
        len += 1
        if(t == i):
            #print(i,",",len)
            if(len == 2):
                print(chain)
                print(i+1)
            break
#print(lenlist.count(2))
#2*82 + 75 + 3*3 + 1*8
'''


#验证函数
'''
        tt = [0 for k in range(256)]
        for k in range(256):
            tt[k] = P[P[k]] + 1
        for k in range(256):
            if(tt[k]!= c[k]):
                print(k)
        exit()
'''

chain1 = [9,12,23,27,166,204,218,219]
group_size = 2
num_groups = 4
all_groupings = list(combinations(chain1, 2))

def generate_groupings(chain1, group_size, num_groups):
    if num_groups == 1:
        yield [chain1]
    else:
        for combo in combinations(chain1, group_size):
            remaining_chain1 = [e for e in chain1 if e not in combo]
            for rest_grouping in generate_groupings(remaining_chain1, group_size, num_groups - 1):
                yield [list(combo)] + rest_grouping

chain1r = list(generate_groupings(chain1, group_size, num_groups))


n = [18, 188, 48, 47, 100, 234, 225, 8, 187, 34, 124, 113, 118, 252, 137, 196, 125, 20, 251, 168, 167, 5, 225, 134, 66, 203, 26, 148, 63, 181, 213, 124, 170, 234, 35, 120, 47, 69, 157, 69, 194]
c = [41, 124, 256, 27, 201, 93, 40, 133, 47, 10, 69, 253, 13, 245, 165, 166, 118, 230, 197, 249, 115, 18, 71, 24, 100, 14, 160, 28, 251, 96, 106, 5, 244, 58, 67, 44, 150, 42, 255, 74, 168, 182, 153, 209, 227, 232, 159, 128, 125, 11, 135, 90, 76, 30, 84, 31, 1, 149, 48, 95, 216, 94, 157, 131, 196, 172, 105, 169, 202, 203, 121, 210, 53, 9, 147, 89, 39, 68, 59, 141, 87, 207, 51, 180, 19, 81, 57, 103, 228, 77, 12, 129, 185, 85, 45, 123, 50, 116, 65, 213, 104, 64, 54, 155, 222, 112, 3, 252, 21, 33, 138, 151, 211, 233, 204, 97, 239, 113, 82, 200, 23, 231, 177, 26, 72, 4, 78, 183, 199, 6, 49, 29, 250, 119, 32, 56, 110, 187, 35, 143, 83, 25, 70, 2, 66, 101, 217, 120, 224, 142, 191, 136, 189, 127, 132, 36, 174, 146, 152, 140, 193, 62, 178, 17, 148, 248, 167, 88, 73, 229, 134, 156, 158, 60, 63, 242, 221, 34, 214, 20, 171, 139, 226, 186, 164, 181, 236, 107, 111, 61, 99, 108, 179, 223, 137, 212, 237, 102, 161, 145, 184, 173, 247, 162, 205, 154, 55, 117, 254, 38, 75, 234, 7, 46, 109, 22, 175, 144, 219, 220, 195, 190, 98, 79, 15, 170, 80, 235, 52, 8, 37, 243, 198, 86, 43, 192, 241, 240, 208, 130, 188, 114, 218, 215, 206, 176, 238, 16, 246, 126, 122, 163, 225, 92, 91, 194]

chain821 = [193, 222, 97, 115, 96, 49, 10, 68, 201, 172, 157, 145, 100, 103, 154, 131, 28, 250, 121, 230, 36, 149, 141, 24, 99, 212, 6, 39, 73, 8, 46, 158, 151, 135, 55, 30, 105, 111, 150, 190, 98, 64, 195, 211, 233, 85, 80, 86, 56, 0, 40, 167, 87, 102, 53, 29, 95, 122, 176, 220, 194, 136, 109, 32, 243, 214, 108, 20, 114, 203, 161, 61, 93, 84, 18, 196, 236, 240, 187, 106, 2, 255]
chain822 = [125, 3, 26, 159, 139, 142, 69, 202, 246, 237, 239, 129, 5, 92, 184, 163, 16, 117, 112, 210, 74, 146, 216, 174, 62, 156, 173, 59, 94, 44, 226, 79, 140, 82, 50, 134, 31, 4, 200, 183, 185, 180, 170, 133, 118, 81, 206, 54, 83, 179, 19, 248, 245, 175, 241, 113, 232, 197, 101, 63, 130, 48, 124, 71, 209, 37, 41, 181, 138, 34, 66, 104, 221, 189, 60, 215, 21, 17, 229, 7, 132, 249]
chain75 = [90, 11, 252, 224, 14, 164, 147, 119, 199, 144, 65, 171, 155, 35, 43, 208, 253, 91, 128, 198, 160, 192, 178, 213, 45, 231, 242, 217, 143, 1, 123, 25, 13, 244, 205, 153, 126, 77, 67, 168, 72, 52, 75, 88, 227, 234, 42, 152, 188, 110, 137, 186, 235, 191, 107, 251, 162, 177, 33, 57, 148, 223, 78, 58, 47, 127, 182, 225, 169, 228, 51, 89, 76, 38, 254]
chain31 = [15, 165, 247]
chain32 = [207, 116, 238]
chain33 = [120, 22, 70]
chain1 = [9,12,23,27,166,204,218,219]

locdic = {}

#处理chain3(四种情况)
#情况1：3个三环
if(0):
    chain31r = [15, 247, 165]
    chain32r = [207, 238, 116]
    chain33r = [120, 70, 22]
    #添加入位置字典
    for i in range(3):
        locdic[chain31r[i]] = chain31r[(i+1)%3]
        locdic[chain32r[i]] = chain32r[(i+1)%3]
        locdic[chain33r[i]] = chain33r[(i+1)%3]

#情况2:1个三环,1个六环
if(1):
    chain31r = [15, 247, 165]
    chain6r = [0 for j in range(6)]
    for j in range(6):
        if(j % 2 == 0):
            chain6r[j] = chain32[j//2]
        else:
            chain6r[j] = chain33[(j//2 + 0) % 6] 
    #添加入位置字典
    for i in range(3):
        locdic[chain31r[i]] = chain31r[(i+1)%3]
    for i in range(6):
        locdic[chain6r[i]] = chain6r[(i+1)%6]

if(0):
    chain32r = [120, 70, 22]
    chain6r = [0 for j in range(6)]
    for j in range(6):
        if(j % 2 == 0):
            chain6r[j] = chain31[j//2]
        else:
            chain6r[j] = chain33[(j//2 + 0) % 6] 
    #添加入位置字典
    for i in range(3):
        locdic[chain32r[i]] = chain32r[(i+1)%3]
    for i in range(6):
        locdic[chain6r[i]] = chain6r[(i+1)%6]

if(0):
    chain33r = [120, 70, 22]
    chain6r = [0 for j in range(6)]
    for j in range(6):
        if(j % 2 == 0):
            chain6r[j] = chain31[j//2]
        else:
            chain6r[j] = chain32[(j//2 + 0) % 6] 
    #添加入位置字典
    for i in range(3):
        locdic[chain33r[i]] = chain33r[(i+1)%3]
    for i in range(6):
        locdic[chain6r[i]] = chain6r[(i+1)%6]

#处理chain75(确定)
chain75r = [0 for i in range(75)]
for i in range(75):
    chain75r[2*i%75] = chain75[i]
#添加入位置字典
for i in range(75):
    locdic[chain75r[i]] = chain75r[(i+1)%75]

#嗯造剩下两种环的组合
for i in range(82):
    print(i)
    #造一个副本
    locdic1 = locdic
    chain164r = [0 for j in range(164)]
    for j in range(164):
        if(j % 2 == 0):
            chain164r[j] = chain821[j//2]
        else:
            chain164r[j] = chain822[(j//2 + i) % 82] 
    #添加入位置字典
    for i in range(164):
        locdic1[chain164r[i]] = chain164r[(i+1)%164]
      
    #4个二元环（包含单环情况）
    for mm in range(16):
        ttt = bin(mm)[2:].zfill(4)
        for j in range(len(chain1r)):
            locdic2 = locdic1
            if(ttt[0] == "1"):
                locdic2[chain1r[j][0][0]] = chain1r[j][0][1]
                locdic2[chain1r[j][0][1]] = chain1r[j][0][0]
            else:
                locdic2[chain1r[j][0][0]] = chain1r[j][0][0]
                locdic2[chain1r[j][0][1]] = chain1r[j][0][1]
            if(ttt[1] == "1"):
                locdic2[chain1r[j][1][0]] = chain1r[j][1][1]
                locdic2[chain1r[j][1][1]] = chain1r[j][1][0]
            else:
                locdic2[chain1r[j][1][0]] = chain1r[j][1][0]
                locdic2[chain1r[j][1][1]] = chain1r[j][1][1]
            if(ttt[2] == "1"):
                locdic2[chain1r[j][2][0]] = chain1r[j][2][1]
                locdic2[chain1r[j][2][1]] = chain1r[j][2][0]
            else:
                locdic2[chain1r[j][2][0]] = chain1r[j][2][0]
                locdic2[chain1r[j][2][1]] = chain1r[j][2][1]
            if(ttt[3] == "1"):
                locdic2[chain1r[j][3][0]] = chain1r[j][3][1]
                locdic2[chain1r[j][3][1]] = chain1r[j][3][0]
            else:
                locdic2[chain1r[j][3][0]] = chain1r[j][3][0]
                locdic2[chain1r[j][3][1]] = chain1r[j][3][1]
            P = [locdic2[j]+1 for j in range(256)]
            
            t = ""
            for x,y in zip(hashlib.sha512(str(P).encode()).digest(), n):
                if((x^y)>=32 and (x^y)<=127):
                    t+=chr(x^y)
                else:
                    break
            if(len(t) > 10):
                print(t)
                exit()
                
#brics+{ab99943f6dae4f20595c8645fcf8289e}

脚本比较丑，只能就题论题，不能作为该类求平方根置换的通解。



prng(加强版)

(题目具体名称并不是这个，只是我还没有找到对应题目名，就先用着)

题目来源：江苏省领航杯

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.number import *
from secret import flag
import random

def base(n, l):
    bb = []
    while n > 0:
        n, r = divmod(n, l)
        bb.append(r)
    return ''.join(str(d) for d in bb[::-1])

def prng(secret):
	seed = base(secret, 5)
	seed = [int(i) for i in list(seed)]
	length = len(seed)
	R = [[ random.randint(0,4) for _ in range(length)] for _ in range(length**2)]
	S = []
	for r in R:
		s = 0
		for index in range(length):
			s += (r[index] + seed[index]) % 5
		s %= 2
		S.append(s)
	return R, S

m = bytes_to_long(flag)
R, S = prng(m)

with open('output.txt', 'w') as f:
	f.write(f'R = {R}\nS = {S}')

梳理加密流程：

  • 将flag转为大整数后，将该整数转为五进制数，并转为列表，作为seed
  • 记列表seed长度为n
  • 生成一个 $ n^2*n$ 的矩阵R，其中每个元素为0-4的随机数
  • 利用R矩阵，对seed矩阵做如下加密：(其中，$ i=1,2…n^2$)
  • 将 $ s_i$ 拼接为S向量后，提供R与S，求解明文

自己做是一点思路都没有，最终找到了 ZM.J 师傅的一篇wp，发现题目是类似的：

[CryptoCTF] CryptoCTF 2023 tough分类 团队解题writeup - 知乎 (zhihu.com)

于是就可以迁移到这道题目中来：

首先，由于seed中每个数字都是0-4之中的某个数m，我们可以先对其进行编码：

1
2
3
4
5
0 : (1,0,0,0,0)
1 : (0,1,0,0,0)
2 : (0,0,1,0,0)
3 : (0,0,0,1,0)
4 : (0,0,0,0,1)

此时，我们相当于把一个0-4的数转化为了五个变量组成的一个向量：

其中，每个变量 $ x_i$ 只有0或1两种取值，并且对于任意一个0-4的数m， $ x_i$ 有且仅有一个变量为1，其他均为0

这么做的意义是什么？是让我们能够将这个先模5再模2的没有办法解的线性方程组，变化到一个可以解的形式。

为什么这样变换后就可以解？由加密流程知道，$ r_{ij},seed_i$ 均为0-4之间的数，因此相加后模5模2的结果完全可以用一张表加以表示：

0 1 2 3 4
0 0 1 0 1 0
1 1 0 1 0 0
2 0 1 0 0 1
3 1 0 0 1 0
4 0 0 1 0 1

表的含义是，当 r 取 i ，seed 取 j 时，表中第 i 行第 j 列即为$ (r+seed)\;(mod\;5)\;(mod\;2)$ 的值

然后在这里举个简单的例子来看一下如何变换原题目的线性方程到这种形式下：

假设$ s = (2+m_0)+(3+m_1)+(4+m_2) \;(mod\;5)\;(mod\;2)$，

第一步，把每个 $ m_i$ 表示为五个变量的形式：

第二步，把每一个r转化成对应系数矩阵：

比如，r=2时，看上表的取2的行，需要变量1或4取1就能得到1，否则为0；r=3时，看上表的取3的行，需要变量0或3取1就能得到1，否则为0；r=4时，看上表的取4的行，需要变量2或4取1就能得到1，否则为0

这又是什么意思呢？比如 $ (2+1) \;(mod\;5)\;(mod\;2)$，由真值表可知，他就完全等价于下面的形式：

这么做的好处就是：

  • 去除了模5的影响
  • 由加法转成了乘法，变成了矩阵可解的形式

因此，刚才的等式$ s = (2+m_0)+(3+m_1)+(4+m_2) \;(mod\;5)\;(mod\;2)$就彻底去除了与模5的关系，而只剩下模2下的线性关系与变量，变成了下面这种形式：

而把这种形式应用于我们需要求解的问题之中，就可以把seed中原本的n个变量转化成5n个变量，因此只需要从n^2个线性方程中拿出5n个线性线性方程即可解得所有的变量取值，再用刚才对m的编码还原即可。

你可能会发现求解后的向量并不全是刚才的编码形式：

1
2
3
4
5
0 : (1,0,0,0,0)
1 : (0,1,0,0,0)
2 : (0,0,1,0,0)
3 : (0,0,0,1,0)
4 : (0,0,0,0,1)

而出现了：

1
(1,1,1,1,0)

事实上，这是因为我们并没有把刚才说的这一点加入到线性方程组的约束中：

  • 对于任意一个0-4的数m， $ x_i$ 有且仅有一个变量为1，其他均为0

但是影响不大了，因为你大概也能猜到(1,1,1,1,0)对应的就是不加该限制时4的编码，因此对应还原就好

exp.ipynb:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from Crypto.Util.number import *

with open(r'E:\vscode\output4.txt') as f:
    exec(f.read())

n = len(R[0])
A = []
B = []

for i in range(5 * n):
    a = []
    B.append(S[i])
    for j in range(n):
        if (R[i][j] == 0):
            a.extend([0, 1, 0, 1 ,0])
        elif (R[i][j] == 1):
            a.extend([1, 0, 1, 0, 0])
        elif (R[i][j] == 2):
            a.extend([0, 1, 0, 0, 1])
        elif (R[i][j] == 3):
            a.extend([1, 0, 0, 1, 0])
        elif (R[i][j] == 4):
            a.extend([0, 0, 1, 0, 1])
    A.append(a)

A = matrix(GF(2), A)
B = vector(GF(2), B)
x = A.solve_right(B)
#print(x)

flag = []
temp = []
for i in range(n):
    if (x[5*i] == 1) and (x[5*i+1] == 0) and (x[5*i+2] == 0) and (x[5*i+3] == 0) and (x[5*i+4] == 0):
        flag.append("0")
    elif (x[5*i] == 0) and (x[5*i+1] == 1) and (x[5*i+2] == 0) and (x[5*i+3] == 0) and (x[5*i+4] == 0):
        flag.append("1")
    elif (x[5*i] == 0) and (x[5*i+1] == 0) and (x[5*i+2] == 1) and (x[5*i+3] == 0) and (x[5*i+4] == 0):
        flag.append("2")
    elif (x[5*i] == 0) and (x[5*i+1] == 0) and (x[5*i+2] == 0) and (x[5*i+3] == 1) and (x[5*i+4] == 0):
        flag.append("3")
    elif (x[5*i] == 0) and (x[5*i+1] == 0) and (x[5*i+2] == 0) and (x[5*i+3] == 0) and (x[5*i+4] == 1):
        flag.append("4")
    elif (x[5*i] == 1) and (x[5*i+1] == 1) and (x[5*i+2] == 1) and (x[5*i+3] == 1) and (x[5*i+4] == 0):
        flag.append("4")

flag = "".join(flag)
flag = long_to_bytes(int(flag, 5))
print(flag)

#CnHongKe{179bdc38ea135c35f1f973c039a422a7}

(有不懂的地方欢迎与我交流！)



ahead

题目来源：暂不明确

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
from random import randint
from os import urandom
from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes
from binascii import unhexlify
from secret import flag
import signal

def gen(S, B):
    L = S[0] ^ S[7] ^ S[38] ^ S[70] ^ S[81] ^ S[96]
    N = S[0] ^ B[0] ^ B[26] ^ B[56] ^ B[91] ^ B[96] ^ (B[3] & B[67]) ^ \
        (B[11] & B[13]) ^ (B[17] & B[18]) ^ (B[27] & B[59]) ^ (B[40] & B[48]) ^ \
        (B[61] & B[65]) ^ (B[68] & B[84]) ^ (B[22] & B[24] & B[25]) ^ \
        (B[70] & B[78] & B[82]) ^ (B[88] & B[92] & B[93] & B[95])
    for j in range(128):
        if j <= 126:
            S[j] = S[j + 1]
            B[j] = B[j + 1]
        else:
            S[127] = L
            B[127] = N
    h = (B[12] & S[8]) ^ (S[13] & S[20]) ^ (B[95] & S[42]) ^ (S[60] & S[79]) ^ \
        (B[12] & B[95] & S[94])
    z = h ^ S[93] ^ B[2] ^ B[15] ^ B[36] ^ B[45] ^ B[64] ^ B[73] ^ B[89]
    return z

S1 = [randint(0, 1) for i in range(128)]
B1 = [randint(0, 1) for i in range(128)]
hint = []
for i in range(40):
    while 1:
        tmp = randint(1, 120)
        if tmp not in hint:
            hint.append(tmp)
            break

print(f"{S1}")
print(f"{hint}")
hint2 = []
for i in range(128):
    if i not in hint:
        hint2.append(B1[i])

print(f"{hint2}")
z = []
for i in range(128):
    z.append(gen(S1, B1))
print(f"{z}")

key = ""
for i in range(128):
    key += str(gen(S1, B1))
key = long_to_bytes(int(key, 2))
iv = urandom(16)
secret = urandom(16)
aes = AES.new(bytes(key), AES.MODE_CBC, iv)
enc_secret = aes.encrypt(secret)
print(f"{iv.hex()}||{enc_secret.hex()}")
input_secret = input("my secret?").strip().encode()
if unhexlify(input_secret) == secret:
    print(flag)
else:
    print("wrong")

仍然是一个师傅问我的没有靶机的交互题，因此也只说思路。题目看着很复杂，简单梳理一下流程：

  • 生成一个初始的S、B，均为长度为128的0、1数组
  • 给出初始S的全部值，以及初始B的88个值
  • 然后以S、B数组为初始值，经过gen函数连续生成128个值作为z数组，并给出z数组
  • 然后继续生成128个值作为AES的key，并加密一个secret，给出密文与iv。如果我们能输入正确的secret就能得到flag

那么显然，如果我们有完整的初始B，就可以直接用他的gen函数生成出key，就能解AES。而现在B被隐藏了40个值，但是却给出了包含了128个初始S、B经gen函数生成的值的数组z。而gen函数看着很麻烦，实际上就是一个复杂LFSR的更新过程，所以其实也可以看作是模2下的一些简单运算。

因此，我们把隐去的40个值视作40个变量，实际上就是40个变量、128个方程的解方程问题。

而这种位运算的多变量方程，z3往往是很有效的。我也直接丢给z3就得到了解，本地测试如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
from random import randint
from z3 import *

def gen(S, B):
    L = S[0] ^ S[7] ^ S[38] ^ S[70] ^ S[81] ^ S[96]
    N = S[0] ^ B[0] ^ B[26] ^ B[56] ^ B[91] ^ B[96] ^ (B[3] & B[67]) ^ \
        (B[11] & B[13]) ^ (B[17] & B[18]) ^ (B[27] & B[59]) ^ (B[40] & B[48]) ^ \
        (B[61] & B[65]) ^ (B[68] & B[84]) ^ (B[22] & B[24] & B[25]) ^ \
        (B[70] & B[78] & B[82]) ^ (B[88] & B[92] & B[93] & B[95])
    for j in range(128):
        if j <= 126:
            S[j] = S[j + 1]
            B[j] = B[j + 1]
        else:
            S[127] = L
            B[127] = N
    h = (B[12] & S[8]) ^ (S[13] & S[20]) ^ (B[95] & S[42]) ^ (S[60] & S[79]) ^ \
        (B[12] & B[95] & S[94])
    z = h ^ S[93] ^ B[2] ^ B[15] ^ B[36] ^ B[45] ^ B[64] ^ B[73] ^ B[89]
    return z

S1 = [randint(0, 1) for i in range(128)]
B1 = [randint(0, 1) for i in range(128)]
S = [0 for i in range(128)]
BB = [0 for i in range(128)]
for i in range(128):
    S[i] = S1[i]
    BB[i] = B1[i]

hint = []
for i in range(40):
    while 1:
        tmp = randint(1, 120)
        if tmp not in hint:
            hint.append(tmp)
            break
hint2 = []
for i in range(128):
    if i not in hint:
        hint2.append(B1[i])

z = []
for i in range(128):
    z.append(gen(S1, B1))


#z3solve
def z3_solve():
    B = [BitVec(f'B_{i}', 1) for i in range(128)]
    solver = Solver()
    j = 0
    for i in range(128):
        if i not in hint:
            B[i] = hint2[j]
            j += 1
    #print(B)
    for i in range(128):
        solver.add(gen(S, B) == z[i])
    if solver.check()==sat:
        print(solver.model())

z3_solve()
print(BB)

那么还原出B后，用初始S、B先生成z，再生成key就能得到AES密钥，就能解密文了。



e20k

题目来源：N1CTF 2023

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
#!/usr/bin/sage
from Crypto.Util.Padding import pad
from Crypto.Util.number import *
from Crypto.Cipher import AES
from hashlib import md5
import signal
import random
import os
FLAG = os.environ.get('FLAG', 'n1ctf{XXXXFAKE_FLAGXXXX}')

class ECPrng:
    def __init__(self):
        self.N = self.keygen()
        self.E = EllipticCurve(Zmod(self.N), [3, 7])
        self.bias = random.randint(1, 2^128)
        self.state = None
        print(f"N = {self.N}")
        
    def keygen(self):
        P = getPrime(256)
        while True:
            q = getPrime(256)
            if is_prime(2*q-1):
                Q = 2*q^2-q
                return P*Q
    
    def setState(self, x0, y0):
        self.state = self.E(x0, y0)
    
    def next(self):
        self.state = 4*self.state
        return int(self.state.xy()[0])+self.bias

def v2l(v):
    tp = []
    for item in v:
        tp.append(item.list())
    return tp

def Sample(eta, num, signal=0):
    if signal:
        random.seed(prng.next())
    s = []
    for _ in range(num):
        if random.random() < eta:
            s.append(1)
        else:
            s.append(0)
    return Rq(s)

class P:
    def __init__(self, A, s, t):
        self.A = A
        self.s = s
        self.t = t
        self.y = None
    
    def generateCommit(self, Verifier):
        self.y = vector(Rq, [Sample(0.3, N, 1) for _ in range(m)])
        w = self.A * self.y
        Verifier.w = w
        print(f"w = {w.list()}")
        
    def generateProof(self, Verifier, c):
        z = self.s*c + self.y
        print(f"z = {v2l(z)}")
        Verifier.verifyProof(z)

class V:
    def __init__(self, A, t):
        self.A = A
        self.t = t
        self.w = None
        self.c = None
        
    def challenge(self, Prover):
        self.c = Sample(0.3, N)
        print(f"c = {self.c.list()}")
        Prover.generateProof(self, self.c)
        
    def verifyProof(self, z):
        if self.A*z == self.t*self.c + self.w:
            return True
        return False

def Protocol(A, secret, t):
    prover = P(A, secret, t)
    verifier = V(A, t)
    prover.generateCommit(verifier)
    verifier.challenge(prover)

if __name__ == "__main__":
    try:
        signal.alarm(120)
        print("ECPRNG init ...")
        prng = ECPrng()
        x0, y0 = input("PLZ SET PRNG SEED > ").split(',')
        prng.setState(int(x0), int(y0))
        N, q, m = (256, 4197821, 15)
        PRq.<a> = PolynomialRing(Zmod(q))
        Rq = PRq.quotient(a^N + 1, 'x')
        A = vector(Rq, [Rq.random_element() for _ in range(m)])
        secret = vector(Rq, [Sample(0.3, N) for _ in range(m)])
        t = A*secret
        print(f"A = {v2l(A)}")
        print(f"t = {t.list()}")
        Protocol(A, secret, t)
        cipher = AES.new(md5(str(secret).encode()).digest(), mode=AES.MODE_ECB)
        print(f"ct = {cipher.encrypt(pad(FLAG.encode(), 16)).hex()}")
    except:
        print("error!")

e20k，0k代表零知识证明(Zero-Knowledge Proof)，简要一点说的话，零知识证明就是一方向另一方证明他知道某个问题的答案，但在证明过程中却不透露答案的任何信息。对于零知识证明，有一篇描述的很通俗的科普类的文章可以参考：

零知识证明Zero-Knowledge Proof介绍 - 知乎 (zhihu.com)

而本题就围绕着一个零知识证明的协议展开，接下来梳理一下题目流程。

连接上靶机后，题目首先会生成一个基于ECC的PRNG，其方程为：

其中N由三个素数组成，并且满足：

然后需要我们提供曲线上的一个点P作为初始state，后续更新state的方式为：

然后用这个PRNG取伪随机数的方式，是取P点的横坐标并加上一个2^128以下的未知的固定偏差bias。

这个ECPRNG初始化完毕后，题目生成一个商环如下：

其中的参数是已知的，分别是(注意与ECPRNG里的q和N区分开)：

1
N, q, m = (256, 4197821, 15)

其中m表示后面的向量长度。

然后题目会生成两个向量A和secret，这里写个例子应该更清晰一点，因为我自己做这个题目的时候就很昏。

具体来说，A是一个如下的长为15的向量：

其中每个元素Ai是Rq中的随机多项式，长这个样子：

1
356602*x^255 + 4017611*x^254 + 3758030*x^253 + ... + 3299775*x^2 + 874450*x + 4059361

而secret是一个用Sample生成的长为15的向量(signal=0)：

其中每个元素si是Rq中的系数仅有01，且1占比约为0.3的多项式，长这个样子：

1
x^253 + x^252 + x^250 + ... + x^5 + x^3 + 1

然后靶机计算向量A和secret的内积，记为t，也就是：

但secret靶机是不会给我们的，因为其md5值会作为后来AES加密flag的密钥，但是靶机会给到我们A和t。在这之后，题目就会进入到本题的零知识证明的协议中，具体来说如下：

首先，证明方(prover)生成一个同样用Sample生成的长为15的向量y(与secret区别在于signal=1)，计算出A和y的内积w，并同时给到我们和验证方：

在此之后，验证方(verifier)进行一次challenge(也就是零知识证明中，验证方要求证明方证明他拥有正确答案而发起的挑战)，challenge的内容是，生成一个用Sample生成的多项式c(和secret中每个元素的生成方式相同，signal=0)，并给到我们和证明方。证明方接收到本次挑战中的c后，需要用如下方式计算出一个向量z：

z也就可以说是证明方的证明材料，证明方将z发送给我们和验证方，验证方通过验证：

来检验证明方是否真的知道secret的值。

简单说一下这个零知识证明的协议为什么正确，我们将上方的式子代入到最后一个表达式中，就有：

所以其正确性是显然的，这说明证明方的确知道secret，否则z会是错误的。而证明方发送给验证方的消息有z和w。w很明显没有泄露secret的任何信息，而显然也没有办法通过向量z计算出secret，所以可以认为，证明方没有泄露任何有关secret的信息。这也就满足了我们刚才提到的零知识证明的目的：

一方向另一方证明他知道某个问题的答案，但在证明过程中却不透露答案的任何信息。

整个协议结束后，靶机将flag用secret的md5值作为AES密钥进行加密，并给出密文。因此，我们的任务就是在上述全部题目流程中，找到可利用点，从而计算出secret的值去进行AES解密。这大概可以分为以下几步：

获取ECC上的点

从上面的题目流程可以知道，我们需要提供一个ECC上的点用于初始化state。然而这个ECC是在模N下的，难以求解其上的二次剩余，所以也就很难得到其上某个点的坐标，因此我们第一步就是要分解N，而分解N的利用点就在于其三个素数的生成方式：

也就是：

敏锐一点的话可以看出其实能构造出一个更合理的形式：

而r也是个素数，所以式子用p、r来表示可以写作：

到这里就和sus那个题目的分解方式一模一样了，只是：

所以也就是从构造一个阶为r^3-1的乘法群，变到构造一个阶为r^2-1的乘法群而已。具体分解过程可以见：

Crypto趣题-RSA(一) | 糖醋小鸡块的blog (tangcuxiaojikuai.xyz)

得到N的分解后，我们就可以在以下三个曲线上分别找点，并crt起来就能得到题目里模N下的ECC上的点了。

利用next

next的过程是：

而如果我们能找到一个阶为3的点的话，那么就有：

就能达到一个目的：每次得到的随机数都相同，而如果每次生成的随机数均相同的话，对于Sample用signal=1生成的向量y来说，由于signal为1时会用next设置种子，因此y中的15个元素均是相同值。

而为了找到模N曲线下阶为3的点P，我们只需要在三条子曲线上分别找到阶为3的点，并crt起来就可以得到所需要的阶为3的P点。而在子曲线上找阶为3的点也很简单，以在模p的曲线上为例，我们只需要先找到其上的一个生成元Gp，并计算：

就可以得到模p曲线上阶为3的点了，但这就要求Ep的阶有3这个因子。同理，Eq、Er的阶必须都要有3，我们才能找到需要的点P。因此我们成功的概率仅有1/27，不满足时就要刷掉重来。

得到这样的P点后，y向量虽然未知，但是我们能知道的一点是：y向量中的15个元素全是相同的。

求y

因为y中15个元素均相同，记为y0，这时候再回看刚才的w的计算过程：

展开写这个向量内积，也就是：

也就是：

而我们又有w和A，因此就可以求出y0的值，也就得到了整个y向量。

求secret

有y向量后，由于我们知道z向量的值以及其计算方式：

所以直接就能得到secret值了。得到secret后就能求md5得到AES密钥，进而解密得到flag。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
from Pwn4Sage.pwn import *
from sympy.ntheory.modular import crt
from Crypto.Cipher import AES
from hashlib import md5
from Crypto.Util.number import *
import ast

while(1):
    sh = remote("node4.anna.nssctf.cn",28855)
    sh.recvuntil(b"N = ")
    N = int(sh.recvline().strip().decode())

    #part1 factor N
    n = 2*N  # n = r(r+1)p
    R = Zmod(N)["x"]
    while(1):
        Q = R.quo(R.random_element(2))
        r = GCD(ZZ(list(Q.random_element() ^ n)[1]), N)
        if(r != 1):
            q = (r+1) // 2
            p = N // q // r
            break


    #part2 get a point whose order is 3
    Ep = EllipticCurve(Zmod(p),[3,7])
    Eq = EllipticCurve(Zmod(q),[3,7])
    Er = EllipticCurve(Zmod(r),[3,7])
    Ep_ord = Ep.order()
    if(Ep_ord % 3 != 0):
        sh.close()
        print("Not this time")
        continue
    Eq_ord = Eq.order()
    if(Eq_ord % 3 != 0):
        sh.close()
        print("Not this time")
        continue
    Er_ord = Er.order()
    if(Er_ord % 3 != 0):
        sh.close()
        print("Not this time")
        continue
    Ep_G = Ep.gens()[0]*(Ep_ord//3)
    Eq_G = Eq.gens()[0]*(Eq_ord//3)
    Er_G = Er.gens()[0]*(Er_ord//3)
    xlist = [int(Ep_G[0]),int(Eq_G[0]),int(Er_G[0])]
    ylist = [int(Ep_G[1]),int(Eq_G[1]),int(Er_G[1])]
    modlist = [p,q,r]
    E_x = crt(modlist,xlist)[0]
    E_y = crt(modlist,ylist)[0]

    sh.recvuntil(b"PLZ SET PRNG SEED > ")
    sh.sendline(str(E_x).encode()+b","+str(E_y).encode())
    break


#part3 get data
N, q, m = (256, 4197821, 15)
PRq.<a> = PolynomialRing(Zmod(q))
Rq = PRq.quotient(a^N + 1, 'x')
sh.recvuntil(b"A = ")
A = ast.literal_eval(sh.recvline().strip().decode())
sh.recvuntil(b"t = ")
t = ast.literal_eval(sh.recvline().strip().decode())
sh.recvuntil(b"w = ")
w = ast.literal_eval(sh.recvline().strip().decode())
sh.recvuntil(b"c = ")
c = ast.literal_eval(sh.recvline().strip().decode())
sh.recvuntil(b"z = ")
z = ast.literal_eval(sh.recvline().strip().decode())
sh.recvuntil(b"ct = ")
ct = long_to_bytes(int(sh.recvline().strip().decode(),16))

A = vector(Rq, [Rq(Ai) for Ai in A])
t = Rq(t)
w = Rq(w)
c = Rq(c)
z = vector(Rq, [Rq(zi) for zi in z])


#part4 get y and then get secret
sum_A = Rq(0)
for Ai in A:
    sum_A += Ai
y = w*sum_A^(-1)
secret = vector(Rq,[(z[i]-y)*c^(-1) for i in range(len(z))])
cipher = AES.new(md5(str(secret).encode()).digest(), mode=AES.MODE_ECB)
flag = cipher.decrypt(ct)
print(flag)

#NSSCTF{0c4a79b9-545f-484b-9f99-e040c2bd0dc9}

看了maple的博客了解到，其实不需要这个w也能做。这是因为当y相同时，将z向量中的每个元素均与最后一个元素作差，就能消去y的影响。然后接下来就有很多做法，比如由于s是仅由01构成的向量，因此可以通过得到的差值向量的系数看出secret对应幂次的项的系数，然后通过多组统计就能得到secret的完整值；又或者再联立t的产生式子，直接求出差向量过后就可以求出A的和然后解出secret。后面这个方法也就是原题flag中提到的RSIS的解决思路了。

此外还看到几个比较有趣的点：

  • 在利用next那个步骤中，我们其实也可以求阶为5的P点，这是因为当阶为5时，有：

  • 而P和-P的横坐标是相同的，所以ECPRNG产生的所有伪随机数仍然相同

  • 商环下的多项式卷积运算应该是可以写成矩阵形式的，因此可能可以造格，然后用LLL直接规约出secret。但问题在于格的维度太大且q(4197821)不够大所以没有特别好的效果



shamir-for-dummies

题目来源：b01lersCTF 2024

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
import os
import sys
import time
import math
import random
from Crypto.Util.number import getPrime, isPrime, bytes_to_long, long_to_bytes

def polynomial_evaluation(coefficients, x):
	at_x = 0
	for i in range(len(coefficients)):
		at_x += coefficients[i] * (x ** i)
		at_x = at_x % p
	return at_x

flag = b'bctf{REDACTED}'

print("")
print("Thanks for coming in. I can really use your help.\n")
print("Like I said, my friend can only do additions. He technically can do division but he says he can only do it once a day.")
print("")
print("I need to share my secret using Shamir secret sharing. Can you craft the shares, in a way that my friend can recover it?\n")
print("")
print("Don't worry, I have the polynomial and I will do all the math for you.")
print("")

s = bytes_to_long(flag)

n = getPrime(4)
p = getPrime(512)

while p % n != 1:
    p = getPrime(512)

print("Let's use \n")
print("n =", n)
print("k =", n)
print("p =", p)
print("")

coefficients = [s]
for i in range(1, n):
	coefficients.append(random.randint(2, p-1))

print("Okay, I have my polynomial P(X) ready. Let me know when you are ready to generate shares with me.\n")
print("")

evaluation_points = []
shares = []

count = 1
while count < n+1:
	print("Evaluate P(X) at X_{0} =".format(count))
	print("> ", end="")
	eval_point = int(input())
	if eval_point % p == 0:
		print("Lol, nice try. Bye.")
		exit()
		break
	elif eval_point < 0 or eval_point > p:
		print("Let's keep things in mod p. Please choose it again.")
	else:
		if eval_point not in evaluation_points:
			evaluation_points.append(eval_point)
			share = polynomial_evaluation(coefficients, eval_point)
			shares.append(share)
			count += 1
		else:
			print("You used that already. Let's use something else!")

print("Nice! Let's make sure we have enough shares.\n")
assert len(shares) == n
assert len(evaluation_points) == n
print("It looks like we do.\n")
print("By the way, would he have to divide with anything? (Put 1 if he does not have to)")
print("> ", end="")
some_factor = int(input())
print("Good. Let's send those over to him.")

for _ in range(3):
	time.sleep(1)
	print(".")
	sys.stdout.flush()

sum_of_shares = 0

for s_i in shares:
	sum_of_shares += s_i
	sum_of_shares = sum_of_shares % p

sum_of_shares_processed = (sum_of_shares * pow(some_factor, -1, p)) % p

if sum_of_shares_processed == s:
	print("Yep, he got my secret message!\n")
	print("The shares P(X_i)'s were':")
	print(shares)
	print("... Oh no. I think now you'd know the secret also... Thanks again though.")
else:
	print("Sorry, it looks like that didn't work :(")

题目流程有点长，简单说一说：

  • 连接上靶机后，题目随机生成512bit的素数p，以及4bit的素数n，保证p-1是n的倍数
  • 以p为模数，生成一个度为n-1的多项式，其中常数项是secret的值，其余系数为未知随机值
  • 可以与靶机交互，输入n个互不相同的横坐标，靶机会计算输入横坐标对应的多项式值(这里注意偷鸡是不可能的，限制死了只能输入互不相同的0-p的值，并且不能是0和p)
  • 在n个点输入完毕后，靶机并不会返回给我们所有点对(否则就可以直接拉格朗日插值)，而是会计算所有纵坐标的和，记为sum of shares
  • 允许我们输入一个数字some_factor，靶机计算如下值，如果该值与secret相等则会给我们所有点对，由于可以拉格朗日插值，所以满足这个条件也就等价于给了我们flag：

那么现在问题就是：如何构造输入点的横坐标与最后的some_factor，去使得上述计算结果恰好为未知的常数项？

不妨回顾一下shamir密钥分享重建多项式的本质。对于一个度为n-1的多项式，如果能有n个互不相同的点对，那么可以通过解如下矩阵方程得到所有系数ai：

而对于题目来说，其计算的是所有纵坐标的和，也就等价于：

也就可以写成：

最终也就等于：

可以看出，无论我们选的n个横坐标的值究竟是多少，ns这个值永远是存在的，这也侧面说明对于some factor应该选择n才能得到s项。而要使得最终结果是ns，就要使剩余的所有和加起来模p下为0，而显然如果能使每个幂次和加起来均为0的话显然能使这一点成立。

而由于费马小定理的存在，a^(p-1)在模p下总是为1，因此我考虑简单构造等比数列。比如我取：

那么此时，对于所有幂次为1的和就有：

这是个公比为2^(p-1/n)的等比数列求和，其公式为：

同理可以验证剩余所有幂次和也均为0，所以就达到了目的。并且返回点对后也不需要再插值了，计算其和并自己求n的逆元相乘就得到flag。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from Crypto.Util.number import *
from pwn import *

sh = remote("gold.b01le.rs", 5006)

sh.recvuntil(b"n = ")
n = int(sh.recvline().strip().decode())
sh.recvuntil(b"p = ")
p = int(sh.recvline().strip().decode())

ttt = (p - 1) // n
tt = pow(2, ttt, p)
for i in range(n): 
    sh.recvuntil(b"> ")
    sh.sendline(str(pow(tt, i, p)).encode())

sh.recvuntil(b"> ")
sh.sendline(str(n).encode())

sh.recvuntil(b"The shares P(X_i)'s were':\n")
datas = eval(sh.recvline().decode())
res = sum(datas)
print(long_to_bytes((res * inverse(n, p)) % p))


#bctf{P0LYN0m14l_1N_M0d_P_12_73H_P0W3Rh0u23_0F_73H_5h4M1r}

不过在看了休息师傅n次单位根的思路后：

b01lers CTF 2024] crypto/pwn 部分-CSDN博客

突然意识到这题还有更有趣的数学道理在里面，下面来阐述一下。

首先，对于模p下的n次单位根，sage可以用如下方式求解：

1
res = GF(p)(1).nth_root(n, all=True)

但是求解他的意义在哪里呢？这就是因为n次单位根的所有幂次和均为0，很容易就满足了我们刚才的要求，具体原因见下。

将n个n次单位根分别记为xi，那么利用这些单位根可以写出如下因式分解：

而由于等式两侧相同，因此等式两侧对应的所有多项式幂次前的系数均相同。也就是说，左侧x^1,x^2,…x^(n-1)的系数均为0，那么右侧对应幂次也应该均为0。

所以把右侧展开，可以轻松得到第一个幂次和为0的事实：

但是似乎并不能直接推出其他次方的幂次和也为0：

但是可以利用牛顿恒等式间接推出这个事实。关于牛顿恒等式的相关知识我在之前TPCTF的wp中有简单讲到：

2023-TPCTF-wp-crypto | 糖醋小鸡块的blog (tangcuxiaojikuai.xyz)

此处我们依然关注的是如下定理的应用：

image-20240418114003579

将这些符号与本题对应起来，P(x)其实就是x^n-1，其n个根就是上面的所有n次单位根xi，而对这个式子的右侧多项式展开：

可以发现其x^k的对应系数就是上图的ek，而由于等式两侧多项式对应幂次前系数需对应相等的缘故，所以ek(0<k<n)也均为0。同时由于P1我们已经知道其为0了，所以这样往上递推就可以得到n次单位根的所有幂次和都为0的事实。

但是还可以进一步延申，因为有限域中的n次单位根其实构成一个循环群，并且其实显然可以发现，对于任意如下形式的t：

t都是n次单位根(因为显然有t^n=1)。因此当t是该循环群的生成元时，两种做法本质上是完全相同的，可以用如下示例程序简单验证：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from Crypto.Util.number import *

n = getPrime(4)
p = getPrime(512)

while p % n != 1:
    p = getPrime(512)

PR.<x> = PolynomialRing(Zmod(p))
f = PR.random_element(degree=n)

res = set(GF(p)(1).nth_root(n, all=True))

T = []
tt = pow(2,(p-1)//n,p)
for i in range(n):
    T.append(pow(tt,i,p))

print(set(T) == res)

有一定概率输出false，此时是因为tt恰好等于1的缘故。