2023-TPCTF-wp-crypto

没有参加这场比赛，但赛后有不少师傅问我题目，就慢慢复现一下吧，目前复现了三道题目。

blurred memory

题目：

from secret import flag

assert flag[:6] == 'TPCTF{' and flag[-1] == '}'
flag = flag[6:-1]

assert len(set(flag)) == len(flag)

xs = []
for i, c in enumerate(flag):
    xs += [ord(c)] * (i + 1)

p = 257
print('output =', [sum(pow(x, k, p) for x in xs) % p for k in range(1, len(xs) + 1)])

output.txt：

output = [125, 31, 116, 106, 193, 7, 38, 194, 186, 33, 180, 189, 53, 126, 134, 237, 123, 65, 179, 196, 99, 74, 101, 153, 84, 74, 233, 5, 105, 32, 75, 168, 161, 2, 147, 18, 68, 68, 162, 21, 94, 194, 249, 179, 24, 60, 71, 12, 40, 198, 79, 92, 44, 72, 189, 236, 244, 151, 56, 93, 195, 121, 211, 26, 73, 240, 76, 70, 133, 186, 165, 48, 31, 39, 3, 219, 96, 14, 166, 139, 24, 206, 93, 250, 79, 246, 256, 199, 198, 131, 34, 192, 173, 35, 0, 171, 160, 151, 118, 24, 10, 100, 93, 19, 101, 15, 190, 74, 10, 117, 4, 41, 135, 45, 107, 155, 152, 95, 222, 214, 174, 139, 117, 211, 224, 120, 219, 250, 1, 110, 225, 196, 105, 96, 52, 231, 59, 70, 95, 56, 58, 248, 171, 16, 251, 165, 54, 4, 211, 60, 210, 158, 45, 96, 105, 116, 30, 239, 96, 37, 175, 254, 157, 26, 151, 141, 43, 110, 227, 199, 223, 135, 162, 112, 4, 45, 66, 228, 162, 238, 165, 158, 27, 18, 76, 36, 237, 107, 84, 57, 233, 96, 72, 6, 114, 44, 119, 174, 59, 82, 202, 26, 216, 35, 55, 159, 113, 98, 4, 74, 2, 128, 34, 180, 191, 8, 101, 169, 157, 120, 254, 158, 97, 227, 79, 151, 167, 64, 195, 42, 250, 207, 213, 238, 199, 111, 149, 18, 194, 240, 53, 130, 3, 188, 41, 100, 255, 158, 21, 189, 19, 214, 127]

题目将flag除去头尾，保证剩下的字符互不相同，之后以如下形式的等式进行了加密：

$c_1 = x_1 + 2x_2 + 3x_3 + ... + 22x_{22} \quad(mod\;p)$ $c_2 = x_1^2 + 2x_2^2 + 3x_3^2 + ... + 22x_{22}^2 \quad(mod\;p)$ $...$ $c_{253} = x_1^{253} + 2x_2^{253} + 3x_3^{253} + ... + 22x_{22}^{253} \quad(mod\;p)$

其中，x1至x22是待求的flag中的字符值，c1至c253是给定的加密值。我们要利用这些加密值还原flag字符。然而，把这253组等式写成上面这种形式的话，可能反而会对解题产生一点误导，这一点继续往下看就会明白。

解决这个题目需要知道牛顿恒等式这个知识，这个可以参考：

牛顿恒等式Newton’s Identities - 知乎 (zhihu.com)

而在这个题目中，我们主要关注这一点应用：

简单说来，牛顿恒等式提供给了我们一个工具，这个工具的作用有：

1、给定一个多项式：
$P(x) = x^k + a_{k-1}x^{k-1} + ... + a_1x + a_0$
假设它拥有根 $ m_1,m_2,…,m_k$ ，则可以求出所有如下形式的幂次和：
$P_i = m_1^i + m_2^i + m_3^i + ... + m_k^i$
2、给定k个幂次和：
$P_i = m_1^i + m_2^i + m_3^i + ... + m_k^i (1 \leq i \leq k)$
则可以恢复以mi为根的如下多项式的所有系数ai：
$P(x) = x^k + a_{k-1}x^{k-1} + ... + a_1x + a_0$

而这个题目中，我们拥有的是若干组幂次和，因此我们显然想要利用第二个作用，用幂次和恢复一个多项式的所有系数，然后对这个多项式求根，从而得到flag的所有字符。但是我们回看刚才写的253组等式形式：

而我们所希望看见的幂次和的形式是：

$P_i = m_1^i + m_2^i + m_3^i + ... + m_k^i (1 \leq i \leq k)$

也就是说，比起我们所希望看见的幂次和的形式，题目提供的等式多了2，3，…，22这样的系数，看上去好像没有办法处理，这也就是我刚才说的会对解题产生一点误导的形式。事实上，2，3，…，22这些系数并不是题目为增加难度进行的设计，反而是为了帮助我们确定每个字符在flag中的位置！这是因为我们其实可以把253组等式写成下面这种形式：

$c_1 = x_1 + x_2 + x_2 + x_3+ x_3+ x_3 + ... + x_{22} \quad(mod\;p)$ $c_2 = x_1^2 + x_2^2 + x_2^2 + x_3^2 + x_3^2+ x_3^2 + ... +x_{22}^2 \quad(mod\;p)$ $...$ $c_{253} = x_1^{253} + x_2^{253} + x_2^{253} + x_3^{253} + x_3^{253} + x_3^{253} + ... + x_{22}^{253} \quad(mod\;p)$

而这就变成了我们需要的幂次和形式，并且flag的每个字符的位置，正好就是我们转化回的多项式中对应根的重数。因此我们就可以还原flag了。

exp：

from Crypto.Util.number import *

output = [125, 31, 116, 106, 193, 7, 38, 194, 186, 33, 180, 189, 53, 126, 134, 237, 123, 65, 179, 196, 99, 74, 101, 153, 84, 74, 233, 5, 105, 32, 75, 168, 161, 2, 147, 18, 68, 68, 162, 21, 94, 194, 249, 179, 24, 60, 71, 12, 40, 198, 79, 92, 44, 72, 189, 236, 244, 151, 56, 93, 195, 121, 211, 26, 73, 240, 76, 70, 133, 186, 165, 48, 31, 39, 3, 219, 96, 14, 166, 139, 24, 206, 93, 250, 79, 246, 256, 199, 198, 131, 34, 192, 173, 35, 0, 171, 160, 151, 118, 24, 10, 100, 93, 19, 101, 15, 190, 74, 10, 117, 4, 41, 135, 45, 107, 155, 152, 95, 222, 214, 174, 139, 117, 211, 224, 120, 219, 250, 1, 110, 225, 196, 105, 96, 52, 231, 59, 70, 95, 56, 58, 248, 171, 16, 251, 165, 54, 4, 211, 60, 210, 158, 45, 96, 105, 116, 30, 239, 96, 37, 175, 254, 157, 26, 151, 141, 43, 110, 227, 199, 223, 135, 162, 112, 4, 45, 66, 228, 162, 238, 165, 158, 27, 18, 76, 36, 237, 107, 84, 57, 233, 96, 72, 6, 114, 44, 119, 174, 59, 82, 202, 26, 216, 35, 55, 159, 113, 98, 4, 74, 2, 128, 34, 180, 191, 8, 101, 169, 157, 120, 254, 158, 97, 227, 79, 151, 167, 64, 195, 42, 250, 207, 213, 238, 199, 111, 149, 18, 194, 240, 53, 130, 3, 188, 41, 100, 255, 158, 21, 189, 19, 214, 127]
p = 257
P = output

e = []
#get e
for i in range(253):
    temp = 0
    for j in range(i):
        temp += (-1)**j * e[j] * P[i-j-1]
        temp %= p
    
    temp = (P[i] - temp) % p
    ei = temp * inverse((-1)^i*(i+1), p) % p
    e.append(ei)

#get a
a = [1]
for i in range(len(e)):
    a.append((-1)^(i+1) * e[i] % p)

#find roots
PR.<x> = PolynomialRing(Zmod(p))
f = 0
for i in range(253):
    f += x^(253-i)*a[i]
f += a[-1]
res = f.roots()

#get flag
flag = [0 for i in range(22)]
for i in res:
    flag[i[1]-1] = chr(i[0])
print("TPCTF{" + "".join(flag) + "}")


#TPCTF{polyisfun_MJCQz:a^VX"G}

sort-teaser

题目：

import re
from Crypto.Util.number import bytes_to_long
import random

letters=set(bytes(range(65,91)).decode())
class Command:
    def __init__(self, target_var, op, l, r=0):
        self.target_var = target_var
        self.op = op
        self.l = l if l in letters else int(l)
        self.r = r if r in letters else int(r)
    def __str__(self):
        return self.target_var+"="+str(self.l)+((self.op+str(self.r)) if self.op!="=" else "")
    __repr__=__str__

class Computation:
    def __init__(self):
        self.vars={x:0 for x in letters}
    
    def resolve_val(self,symbol):
        return self.vars[symbol] if type(symbol)==str else symbol
    
    def run(self,cmd):
        if cmd.op=='+':
            self.vars[cmd.target_var]=self.resolve_val(cmd.l)+self.resolve_val(cmd.r)
            if self.vars[cmd.target_var].bit_length()>100000:
                raise OverflowError
        elif cmd.op=='-':
            self.vars[cmd.target_var]=self.resolve_val(cmd.l)-self.resolve_val(cmd.r)
            if self.vars[cmd.target_var].bit_length()>100000:
                raise OverflowError
        elif cmd.op=='*':
            self.vars[cmd.target_var]=self.resolve_val(cmd.l)*self.resolve_val(cmd.r)
            if self.vars[cmd.target_var].bit_length()>100000:
                raise OverflowError
        elif cmd.op=='/':
            self.vars[cmd.target_var]=self.resolve_val(cmd.l)//self.resolve_val(cmd.r)
        elif cmd.op=='%':
            self.vars[cmd.target_var]=self.resolve_val(cmd.l)%self.resolve_val(cmd.r)
        elif cmd.op=='&':
            self.vars[cmd.target_var]=self.resolve_val(cmd.l)&self.resolve_val(cmd.r)
        elif cmd.op=='|':
            self.vars[cmd.target_var]=self.resolve_val(cmd.l)|self.resolve_val(cmd.r)
        elif cmd.op=='^':
            self.vars[cmd.target_var]=self.resolve_val(cmd.l)^self.resolve_val(cmd.r)
        elif cmd.op=='<':
            self.vars[cmd.target_var]=int(self.resolve_val(cmd.l)<self.resolve_val(cmd.r))
        elif cmd.op=='>':
            self.vars[cmd.target_var]=int(self.resolve_val(cmd.l)>self.resolve_val(cmd.r))
        elif cmd.op=='<=':
            self.vars[cmd.target_var]=int(self.resolve_val(cmd.l)<=self.resolve_val(cmd.r))
        elif cmd.op=='>=':
            self.vars[cmd.target_var]=int(self.resolve_val(cmd.l)>=self.resolve_val(cmd.r))
        elif cmd.op=='!=':
            self.vars[cmd.target_var]=int(self.resolve_val(cmd.l)!=self.resolve_val(cmd.r))
        elif cmd.op=='==':
            self.vars[cmd.target_var]=int(self.resolve_val(cmd.l)==self.resolve_val(cmd.r))
        elif cmd.op=='<<':
            if self.resolve_val(cmd.l).bit_length()+self.resolve_val(cmd.r)>100000:
                raise OverflowError
            self.vars[cmd.target_var]=int(self.resolve_val(cmd.l)<<self.resolve_val(cmd.r))
        elif cmd.op=='>>':
            self.vars[cmd.target_var]=int(self.resolve_val(cmd.l)>>self.resolve_val(cmd.r))
        elif cmd.op=='=':
            self.vars[cmd.target_var]=self.resolve_val(cmd.l)

def parse_command(cmdstr):
    cmdstr=re.sub("\s","",cmdstr)
    m=re.match("^([A-Z])=([A-Z]|-?\d+)$",cmdstr)
    if m:
        return Command(m[1],"=",m[2])
    m=re.match("^([A-Z])=([A-Z]|-?\d+)([+\-*/%&|^><]|[><!=]=|<<|>>)([A-Z]|-?\d+)$",cmdstr)
    if m:
        return Command(m[1],m[3],m[2],m[4])
    m=re.match("^([A-Z])=-([A-Z])$",cmdstr)
    if m:
        return Command(m[1],"-",0,m[2])
    raise SyntaxError

def run_commands(fun, init_state):
    comp=Computation()
    comp.vars.update(init_state)
    try:
        for i in fun:
            comp.run(i)
    except Exception as e:
        pass # exceptions are suppressed
    return comp.vars

def input_function(line_limit, cmd_limit):
    fun=[]
    while True:
        line = input().strip()
        if line == "EOF":
            break
        if len(line)>line_limit:
            assert False, "command too long"
        fun.append(parse_command(line))
        if len(fun)>cmd_limit:
            assert False, "too many commands"
    return fun

flag=open(f"flag.txt").read().strip()
assert len(flag)<32

print("Enter your function A:")
fun_A=input_function(100,30)


flag_array=list(flag.encode()) # the flag is static
A=[]
B=[]
for i in range(100):
    cur_A=bytes_to_long(bytes(flag_array))
    cur_res=run_commands(fun_A,{"A":cur_A})
    A.append(cur_A)
    B.append(cur_res["B"])
    random.shuffle(flag_array)

assert len(set(B))==1, "results are not same"

target_B=bytes_to_long(bytes(sorted(flag_array)))
if target_B==B[0]:
    print(flag)
else:
    print("You did not sort correctly")
exit(0)

几个sort题目都是基于Command类和Computation类以及几个工具函数开展的，因此先介绍一下这些工具的功能。

Command类：这个类提供了一个运算式的拆分、具体来说，对于一个运算式例如 $A = B + C $，Command类可以将它拆分为目标变量A，二元运算左值B，二元运算符+与二元运算右值C。同时Command类可以用str方法返回这个运算式的字符串形式。

Computation类：这个类提供了三个基本功能：

设置了一个字典，可记录A-Z共26个变量的当前运算结果
可返回当前某个变量的值
可以进行变量之间的运算

parse_command函数：这个函数的功能就是把字符串形式的运算式识别出来，并返回Command类对象。

run_commands函数：这个函数的功能就是执行一串commands形式的计算式，并在全部执行完毕后返回26个变量的计算结果。

明白这些工具的作用之后，我们正式进入题目。题目的任务如下：

首先确保flag长度小于32
然后我们可以输入不超过30行Commands计算式，每一行的长度不超过100。而由于题目中的Commands不支持带括号的嵌套计算(比如A=(A+B)+C)，因此长度不超过100的限制应该主要是防止输入数字过大
之后进行100轮计算，每一轮会把当前的flag_array赋值给A，然后用我们输入的所有Commands计算式进行运算，运算完毕后将B的计算结果添加到列表B中，之后将flag_array打乱，进行下一轮计算
100轮计算完毕后，如果满足每一轮B的运算结果均相同，且均等于排序好的flag_array值，就能得到flag

所以我们需要做的事情是根据题目任务的要求，想办法构造一组Commands指令实现题目目标。

而我的核心思路是利用以下两点：

flag是静态的，也就是多次连接靶机访问到的flag均相同
在100轮计算完毕后，靶机会优先检查B列表的计算值是不是全部相同后，再检查是不是均为排序好的flag_array值

如何利用呢？首先我们可以爆破flag的长度n，为此构造如下的Commands序列：

1 2	C = A >> 8*n B = C

从0开始爆破，如果n恰好等于flag的长度，那么100轮计算中B均为0；而n小于flag的长度的话，B就会是不同值。这就导致靶机返回的信息分别为assert的报错和sort不正确，因此我们可以确定flag的长度。

有了flag的长度后，我们又知道flag头是”TPCTF{“，因此我们就可以逐个爆破flag字符，为此构造如下的Commands序列：

1 2	C = A >> 8*(length-6-i+1) B = C == ("TPCTF{" + n)

其中，i是当前已经爆破出的字符数量，n是我们的爆破值。当n恰好等于当前flag的字符值时，第一次计算得到的B是1；而后面进行了打乱，开头的”TPCTF{“被打乱了，因此B应该均为0。而n不等于当前flag的字符值时，100次计算出的结果B均为0，这就又产生了区别。因此我们就可以逐个还原flag的字符。

同理，已知”}”是flag尾，我们也可以从尾部用&运算逐个爆破。

exp：

from Crypto.Util.number import *
from pwn import *
from tqdm import *

# context.log_level = 'debug'

#get length
if(0):
    for i in range(32):
        r = remote('202.112.238.82', 13371)
        shift = 8*i
        command1 = ("C=A>>" + str(shift)).encode()
        command2 = b"B=C"
        r.recvuntil(b"Enter your function A:")
        r.sendline(command1)
        r.sendline(command2)
        r.sendline(b"EOF")
        r.recvline()
        temp = r.recvline()
        if(b"You did not sort correctly"in temp):
            print(i)
            r.close()
            break
        r.close()

#get flag
length = 29
prefix = b"TPCTF{"
table = [i for i in range(32,128)]
flag = b""
if(1):
    for i in trange(length-6):
        for n in table:
            r = remote('202.112.238.82', 13371)
            shift = 8*(length-6-i-1)
            already = (bytes_to_long(prefix + flag) << 8) + n
            command1 = ("C=A>>" + str(shift)).encode()
            command2 = ("B=C==" + str(already)).encode()
            r.recvuntil(b"Enter your function A:")
            r.sendline(command1)
            r.sendline(command2)
            r.sendline(b"EOF")
            r.recvline()
            temp = r.recvline()
            if(b"You did not sort correctly" not in temp):
                flag += long_to_bytes(n)
                r.close()
                break
            r.close()
print(prefix+flag)

#TPCTF{A_strAnge_s1de_channel}

matrix

题目：

import numpy as np

matrices=[[[16, 55, 40], [0, -39, -40], [0, 55, 56]], [[13, 41, 29], [3, -25, -29], [-3, 41, 45]], [[7, 13, 7], [9, 3, -7], [-9, 13, 23]], [[1, -15, -15], [15, 31, 15], [-15, -15, 1]], [[217, 728, 512], [39, -472, -512], [-39, 728, 768]], [[9341, 41833, 32493], [21635, 96663, 75027], [-29315, -130967, -101651]], [[10, 27, 18], [6, -11, -18], [-6, 27, 34]], [[28, 111, 84], [-12, -95, -84], [12, 111, 100]], [[266, 970, 705], [-10, -714, -705], [10, 970, 961]], [[1878, 4506, 2629], [2218, -410, -2629], [-2218, 4506, 6725]], [[253, 953, 701], [3, -697, -701], [-3, 953, 957]], [[1881, 4520, 2640], [2215, -424, -2640], [-2215, 4520, 6736]], [[233, 821, 589], [23, -565, -589], [-23, 821, 845]], [[1593, 3096, 1504], [2503, 1000, -1504], [-2503, 3096, 5600]], [[-7038, -35490, -28451], [-19586, -98654, -79069], [27266, 137310, 110045]], [[196, 695, 500], [60, -439, -500], [-60, 695, 756]], [[1590, 3082, 1493], [2506, 1014, -1493], [-2506, 3082, 5589]], [[166, 490, 325], [90, -234, -325], [-90, 490, 581]], [[149002, 670490, 521489], [375174, 1688246, 1313071], [-506214, -2277910, -1771695]], [[163, 546, 384], [93, -290, -384], [-93, 546, 640]], [[145, 457, 313], [111, -201, -313], [-111, 457, 569]], [[148969, 670341, 521373], [375207, 1688395, 1313187], [-506247, -2278059, -1771811]], [[178, 606, 429], [78, -350, -429], [-78, 606, 685]], [[9389, 42057, 32669], [21587, 96439, 74851], [-29267, -130743, -101475]], [[46, 195, 150], [-30, -179, -150], [30, 195, 166]], [[4, -1, -4], [12, 17, 4], [-12, -1, 12]], [[-7041, -35504, -28462], [-19583, -98640, -79058], [27263, 137296, 110034]], [[184, 579, 396], [72, -323, -396], [-72, 579, 652]], [[22, 83, 62], [-6, -67, -62], [6, 83, 78]], [[127, 368, 242], [129, -112, -242], [-129, 368, 498]], [[25, 97, 73], [-9, -81, -73], [9, 97, 89]], [[118, 289, 172], [138, -33, -172], [-138, 289, 428]], [[19, 69, 51], [-3, -53, -51], [3, 69, 67]], [[199, 639, 441], [57, -383, -441], [-57, 639, 697]], [[160, 517, 358], [96, -261, -358], [-96, 517, 614]]]


flag=input("Flag (TPCTF{...}): ").strip()
x=int('23'+''.join([f"{i:07b}" for i in flag[6:-1].encode()]),16)
a=np.array([80+256*x,396+1280*x, 317+1024*x])

mi=input("Series of matrices: ").encode()
for i in mi:
    a=np.dot(a,matrices[i-65])
        
if np.dot(a,[84118752460105480846935836819753079271600697690686619664255230678276718877418958891792249030775786942317984652111184426018279427, 89173103422445447876715049689189652193176619520301916283899743110137112860432642548206151350732936688768966032976538813292605444, -132496067393083180057627771316425335059370948823049050270938486557240570794895542908205751446110117596540703704248469623120326662])==0:
    print("Correct")
else:
    print("Wrong")

参考：

TPCTF 2023 matrix wp (done after contest) (github.com)

非常有意思的一道题目。题目代码不长，首先梳理一下其加密过程：

给出一系列矩阵matrices
将flag去掉头尾，然后每个字符转为7位二进制，全部转完后在前面连接上23，最后用十六进制的方式转化为整数值x
以x为基础定义一个向量a
从matrices中选择若干个矩阵(每个矩阵也可能在不同位置被选择若干次)与a作右乘，相乘完毕后，若a与一个目标向量点积为0，则输出”Correct”

那么首先会注意到题目对于flag串的处理很奇怪，他将flag逐字符转为二进制后，却用十六进制将他转为一个整数值，这肯定是之后可以利用的一个点。

回到题目，我们先要找到具体的求解步骤。如果我们可以知道mi到底是选择了哪些矩阵连乘的话，我们就可以计算出最后与目标向量做点积的向量a，从而解方程得到x进而还原flag。

所以我们的核心目标就在于通过某种方式确定mi到底是哪些矩阵。为此我们观察matrices这一系列矩阵的特征，首先计算一下他们的特征值：

matrices=[[[16, 55, 40], [0, -39, -40], [0, 55, 56]], [[13, 41, 29], [3, -25, -29], [-3, 41, 45]], [[7, 13, 7], [9, 3, -7], [-9, 13, 23]], [[1, -15, -15], [15, 31, 15], [-15, -15, 1]], [[217, 728, 512], [39, -472, -512], [-39, 728, 768]], [[9341, 41833, 32493], [21635, 96663, 75027], [-29315, -130967, -101651]], [[10, 27, 18], [6, -11, -18], [-6, 27, 34]], [[28, 111, 84], [-12, -95, -84], [12, 111, 100]], [[266, 970, 705], [-10, -714, -705], [10, 970, 961]], [[1878, 4506, 2629], [2218, -410, -2629], [-2218, 4506, 6725]], [[253, 953, 701], [3, -697, -701], [-3, 953, 957]], [[1881, 4520, 2640], [2215, -424, -2640], [-2215, 4520, 6736]], [[233, 821, 589], [23, -565, -589], [-23, 821, 845]], [[1593, 3096, 1504], [2503, 1000, -1504], [-2503, 3096, 5600]], [[-7038, -35490, -28451], [-19586, -98654, -79069], [27266, 137310, 110045]], [[196, 695, 500], [60, -439, -500], [-60, 695, 756]], [[1590, 3082, 1493], [2506, 1014, -1493], [-2506, 3082, 5589]], [[166, 490, 325], [90, -234, -325], [-90, 490, 581]], [[149002, 670490, 521489], [375174, 1688246, 1313071], [-506214, -2277910, -1771695]], [[163, 546, 384], [93, -290, -384], [-93, 546, 640]], [[145, 457, 313], [111, -201, -313], [-111, 457, 569]], [[148969, 670341, 521373], [375207, 1688395, 1313187], [-506247, -2278059, -1771811]], [[178, 606, 429], [78, -350, -429], [-78, 606, 685]], [[9389, 42057, 32669], [21587, 96439, 74851], [-29267, -130743, -101475]], [[46, 195, 150], [-30, -179, -150], [30, 195, 166]], [[4, -1, -4], [12, 17, 4], [-12, -1, 12]], [[-7041, -35504, -28462], [-19583, -98640, -79058], [27263, 137296, 110034]], [[184, 579, 396], [72, -323, -396], [-72, 579, 652]], [[22, 83, 62], [-6, -67, -62], [6, 83, 78]], [[127, 368, 242], [129, -112, -242], [-129, 368, 498]], [[25, 97, 73], [-9, -81, -73], [9, 97, 89]], [[118, 289, 172], [138, -33, -172], [-138, 289, 428]], [[19, 69, 51], [-3, -53, -51], [3, 69, 67]], [[199, 639, 441], [57, -383, -441], [-57, 639, 697]], [[160, 517, 358], [96, -261, -358], [-96, 517, 614]]]
target = vector(ZZ,[84118752460105480846935836819753079271600697690686619664255230678276718877418958891792249030775786942317984652111184426018279427, 89173103422445447876715049689189652193176619520301916283899743110137112860432642548206151350732936688768966032976538813292605444, -132496067393083180057627771316425335059370948823049050270938486557240570794895542908205751446110117596540703704248469623120326662])

for i in matrices:
    temp = Matrix(ZZ,i)
    print(temp.eigenvalues())

可以发现每个矩阵特征值都是很特殊的，全部为16的幂的形式：

1	[1, 16, 16],[1, 256, 256],[4096, 256, 1]......

这与我们刚才说的对flag的奇怪处理对上了，十六进制一定是一个很重要的点

而对于矩阵连乘，如果我们能够将其通过相似矩阵对角化，使得每个矩阵Mi都变成如下形式：

$M_i = PL_iP^{-1}$

其中Li是对角矩阵，那么连乘的运算可以化成：

$\prod_{i=0}^{n}M_i = \prod_{i=0}^{n}PL_iP^{-1} = P(\prod_{i=0}^{n}L_i)P^{-1}$

也就是说，如果能找到相同的P矩阵去对角化所有矩阵，就能抵消掉很多可逆矩阵的相乘过程，而变成对角线上元素的朴素的数乘过程，因此我们尝试对角化：

1
2
3

for i in matrices:
    temp = Matrix(ZZ,i)
    print(temp.diagonalization())

但是这样会报错，说明矩阵是无法对角化的，之后我尝试化成jordan_form发现无法使矩阵变成ZZ形式，也许是打开方式有问题。

然后出题人赛后给了hint，这一步的P矩阵以及其对应的逆矩阵分别是：

1 2	[[2, 9, 7], [1, 5, 4], [1, 1, 1]] [[1, -2, 1], [3, -5, -1], [-4, 7, 1]]

我们用这两个矩阵对M进行相似处理：

P = Matrix(ZZ,[[2, 9, 7], [1, 5, 4], [1, 1, 1]])
P_inv = Matrix(ZZ,[[1, -2, 1], [3, -5, -1], [-4, 7, 1]])
for i in matrices:
    temp = Matrix(ZZ,i)
    print(P*temp*P_inv)
    print()

这可以将Mi处理成如下的相似矩阵，但不是对角化的：

[16  0  0]
[ 0 16  0]
[ 5  5  1]

[16  0  0]
[ 0 16  0]
[ 4  4  1]

[16  0  0]
[ 0 16  0]
[ 2  2  1]
......

可以发现，处理后的所有矩阵都是如下形式：

$\left(\begin{matrix} 16^x & & \\ & 16^y & \\ a & b & 1\\ \end{matrix}\right)$

到这个时候，我们终于知道一直觉得奇怪的十六进制到底该怎么用了，为了表示方便，我们把题目最后验证点积的的目标向量称作t，因此以最初matrices的一系列形式进行连乘的算式如下：

$aM_iM_j...M_kt = 0$

我们将Mi换成相似表示后的形式：

$L_i = PM_iP^{-1}$

所以有：

$M_i = P^{-1}L_iP$

然后全部代入到连乘式里：

$a(P^{-1}L_iP)(P^{-1}L_jP)...(P^{-1}L_kP)t = 0$

矩阵乘法具有结合律，我们换一种连乘分组：

$(aP^{-1})L_i(PP^{-1})L_j(P...P^{-1})L_k(Pt) = 0$

中间的可逆矩阵相乘均抵消掉，就变成了：

$(aP^{-1})L_iL_j...L_k(Pt) = 0$

而正如刚才所说，Li均为如下形式：

$\left(\begin{matrix} 16^x & & \\ & 16^y & \\ a & b & 1\\ \end{matrix}\right)$

而对任意一个满足如下条件的1x3的向量c与他相乘：

$(c_1,c_2,1) \left(\begin{matrix} 16^x & & \\ & 16^y & \\ a & b & 1\\ \end{matrix}\right)$

得到的向量是：

$(c1*16^x + a,c_2 * 16^y + b,1)$

这其实是一个十六进制串的拼接，因为乘16^x的操作，等价于十六进制串左移x位，+a就等于左移后在低位+a。对于16^y和b同理。

这就是题目最重要的一点，而接下来，注意到我们刚才转化后的矩阵连乘形式中，aP^-1和Pt都是可以计算的：

$(aP^{-1})L_iL_j...L_k(Pt) = 0$

于是我们把他们计算出来：

PR.<x> = PolynomialRing(ZZ)
a = vector([80+256*x,396+1280*x, 317+1024*x])
print(a)
print(a*P_inv)
print(P*target)

计算出的结果完美的符合我们的一切发现：

1
2

aP_inv = (0, 256*x + 79, 1)
Pt = (43322963970637732180912721627235682866194329302747133987038743447103457934462900359999600095377180907771737671271930809827721216, -1, 40795788489467748666023115192517396405406368387939485677216487231173260942956058531792648935398606034546246980839253616190558209)

我们把Pt记为：

1	Pt = (c1,-1,c2)

并且可以发现，c1转化为十六进制其实是：

1	0x10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

也就是将一个十六进制串左移106位。

之后，我们将刚才Li，Lj，……Lk的连乘过程转化为十六进制串的拼接过程，假设aP^-1第一维和第二维分别拼接上的是A和B，那么就有：

$(aP^{-1})L_iL_j...L_k = (0, 256*x + 79, 1)L_iL_j...L_k$

79用十六进制表示为4f，那么得到的向量用十六进制串表示就是，此后我们用或运算符|表示字符串的连接，避免与加法搞混：

$(A,flag|4f|B,1)$

而这个向量与Pt向量点积为0：

$(A,flag|4f|B,1)(c1,-1,c2) = 0$

也就是：

$Ac1 +c2 = flag|4f|B$

而正如我们刚才所说，c1是十六进制串左移106位，那么这个式子最终就表示成了：

$A|c2 = flag|4f|B$

这就以十六进制串连接的形式，构造出了我们最终需要的等式。我们要根据这个等式来想办法求解出A和B，这样就可以确定整个串，从而知道flag的构成。

而回看我们现在的已知条件，我们知道每一个Li中，x、y、a、b的具体值：

$\left(\begin{matrix} 16^x & & \\ & 16^y & \\ a & b & 1\\ \end{matrix}\right)$

也就是说我们知道与乘上每个Li等价的十六进制串连接，举个例子，L0为：

1
2
3

[16  0  0]
[ 0 16  0]
[ 5  5  1]

所以由于x，y均为1，其对应的拼接就是”5”,”5”。而假设有如下矩阵：

1
2
3

[16  0  0]
[ 0 256  0]
[ 5  5  1]

那么x=1，y=2，对应的拼接就为”5”，”05”。

明白了这一点后，我们找出所有Li对应的拼接，并存储起来：

P = Matrix(ZZ,[[2, 9, 7], [1, 5, 4], [1, 1, 1]])
P_inv = Matrix(ZZ,[[1, -2, 1], [3, -5, -1], [-4, 7, 1]])
L = [P*Matrix(ZZ,i)*P_inv for i in matrices]
padding = []
for i in L:
    len1 = len(bin(i[0,0])[2:]) // 4
    len2 = len(bin(i[1,1])[2:]) // 4
    pad1 = hex(i[2,0])[2:].zfill(len1)
    pad2 = hex(i[2,1])[2:].zfill(len2)
    padding.append((pad1,pad2))
print(padding)

padding为：

[('5', '5'), ('4', '4'), ('2', '2'), ('0', '0'), ('61', '16'), ('304', '74'), ('3', '3'), ('9', '9'), ('64', '41'), ('310', '135'), ('34', '94'), ('311', '136'), ('54', '40'), ('301', '036'), ('28', '231'), ('19', '91'), ('300', '035'), ('50', '05'), ('2314', '1'), ('09', '90'), ('08', '80'), ('2304', '0'), ('18', '81'), ('314', '84'), ('f', 'f'), ('1', '1'), ('27', '230'), ('51', '15'), ('7', '7'), ('07', '70'), ('8', '8'), ('29', '23'), ('6', '6'), ('60', '06'), ('17', '71')]

那么接下来怎么入手呢？回看刚才的等式：

$A|c2 = flag|4f|B$

由于我们知道flag的开头连接了一个23，所以进一步拆分为：

$A|c2 = 23|flag|4f|B$

并且c2等于：

1	f111101101010100101001001110111011100101000010100011110001001000111100110101011001001101010111010010101001

可以看出c2是不含4的，因此等式左右两个串各部分的对应关系有两种，一种是：

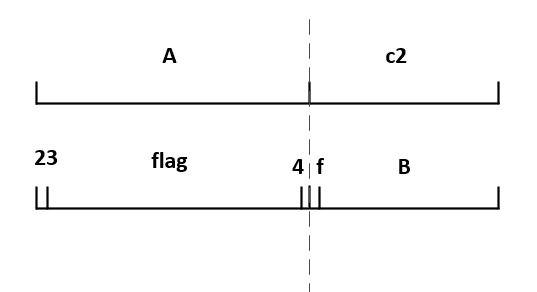
此时我们就可以完全知道B，但也可以发现，这种情况下，我们通过B找不到任何一组符合要求的A，这是因为flag也是全部为0、1的串，而A开头是23，因此对于B的第一个字符1，只能找到下面的这一组padding对应：

1	('2314', '1')

但是4是不在flag里的，因此这种串的长度对应关系不合理，那么合理的对应关系就是：

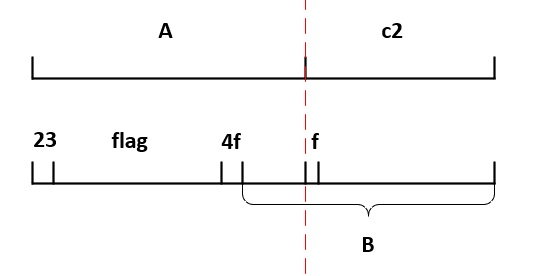
此时我们仅能通过c2知道B的后半部分，但是由于0和1均存在两种对应关系：

1 2	('2304', '0'), ('0', '0') ('2314', '1'), ('1', '1')

并且B的前半部分和A有交集，因此并不是很好从B出发确定每一个padding分别是什么。因此我们转换思路，从A出发。出发的点就是A的开头是23，并且在一系列01串之后以4f结尾。

进一步的，观察上面的padding对应关系，可以发现关于f的部分只有：

1	('f', 'f')

也就是说，A如果某处出现f，B对应的部分一定也是f，所以我们把4f拆开，就又可以对问题进行一点简化：

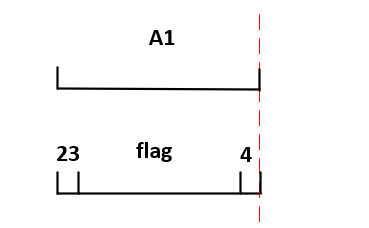
也就是说为了得到flag，我们只需要找到对应的A1部分即可，其中A1部分以23开头，4结尾，并且中间部分全为01。同时我们知道，23开头的padding只有：

1	('2304', '0'), ('2314', '1')

显然都不符合要求，因此要从剩下的padding之中选择，对于2来说可供选择的只有：

1	('2', '2')

同样的道理，4也就只能选择：

1	('4', '4')

而中间只剩下01串，因此也只能选择：

1	('0', '0'), ('1', '1')

但是3可以选择：

1	('300', '035'), ('301', '036'), ('310', '135'), ('311', '136'), ('3', '3')

也就是说，这个推导过程可以以f为分隔，按照如下形式向右推进：

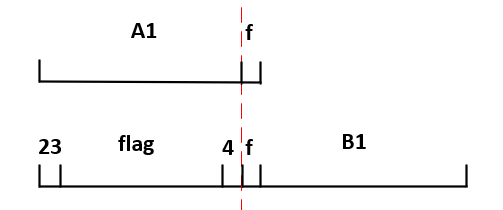
这个推导过程可以一直向右推进，直到Bi=c2则结束，此间Ai=Bi恒成立。

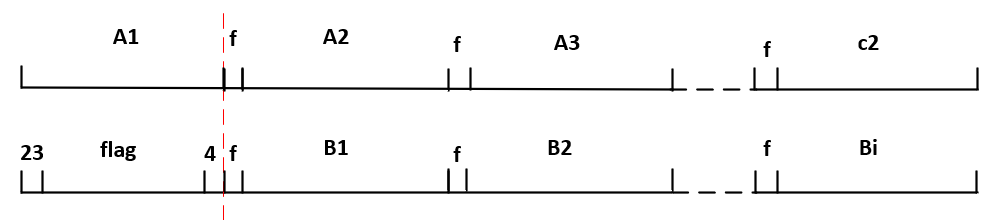
此时就可以看出题目最重要的一点：这个推进过程其实可以看作是A1、A2…、Ai、c2之间的一个逐步的跳转过程，跳转的依据是由矩阵确定的padding规则，跳转的起始点是23|flag|4，结束点是c2。

因此我们现在要做的事情就是：根据这些padding规则来确定出跳转的逻辑，从而找到c2和初始flag的关系，从而还原flag串。为此我们将padding规则分成如下几组分别看看它们的作用：

1	('0', '0'), ('1', '1'), ('2', '2'), ('3', '3'), ('4', '4'), ('5', '5'), ('6', '6'), ('7', '7'), ('8', '8'), ('9', '9'),('f','f')

上面这些是恒等变换，跳转与不跳转没有区别，所以可以不用管

1	('300', '035'), ('301', '036'), ('310', '135'), ('311', '136')

可以看到，如果3后面是连续两个的01串，则将第二个字符变成5或6，并且3向右移动。

1	('304', '74'), ('314', '84'), ('34', '94')

由上一组知道，在推导过程中，3一直在向右移，而A1末尾以4结束。因此这一组规则就是在说，如果3右移到flag串最后，后方仅剩最后一个0或1时，3会和这个0或1一同变成7或8，如果没有数字则会变成9。

1	('50', '05'), ('51', '15'), ('60', '06'), ('61', '16')

这一组是在说，5、6可以越过0、1向右移动。

1	('54', '40'), ('64', '41')

这一组是在说，5、6越过4后会对应变回0、1。也就是5、6到了末尾的4之后，会变回当时被选中的3后方的第二个0或1，此时它就成了c2中的0或1。

1	('07', '70'), ('08', '80'), ('09', '90'), ('17', '71'), ('18', '81'), ('19', '91')

这一组是在说，7、8、9可以越过0、1向左移动。

1	('27', '230'), ('28', '231'), ('29', '23')

这一组是在说，7、8、9如果向前移动直到碰到开始的2时，就会把刚才3在最末尾碰到的0或1相应的还原出来。

1	('2304', '0'), ('2314', '1')

最后一组是在说，仅剩下最后一个数字的时候，消去234，跳转结束。此时完成了A1到c2的全部跳转。

看上去规则很复杂，但是实际上仔细观察，就会发现这些跳转背后的真正含义。首先，3完成类似指针的作用，每次指向后方的第二个0或1，并将他转化为5或6后向后方传递，5和6越过4后，还原回被选中的比特，成为了c2中的比特，完成了这个比特的全部跳转。而7、8、9则是实现一个”环”的功能，他将移动到末尾的指针3重新带回到开头的2后方，开始新一轮的选定。而将所有flag的比特选到仅剩一个时，234就会被消掉，此时彻底完成全部跳转。

这个过程也就可以抽象成：将flag的二进制串首尾相连，从第一个开始向后选择，每次选中当前编号为2的一个比特，放入c2的末尾，然后以当前位置继续向后选择直到全部选中为止。这个过程用一句话概括就是：c2是flag的二进制串进行约瑟夫环逐个选定编号为2的比特的逆序！

因此，我们将c2按照约瑟夫环生成的方式得到下标的索引，然后逐比特还原，就能得到flag了。

exp：

from Crypto.Util.number import *

matrices=[[[16, 55, 40], [0, -39, -40], [0, 55, 56]], [[13, 41, 29], [3, -25, -29], [-3, 41, 45]], [[7, 13, 7], [9, 3, -7], [-9, 13, 23]], [[1, -15, -15], [15, 31, 15], [-15, -15, 1]], [[217, 728, 512], [39, -472, -512], [-39, 728, 768]], [[9341, 41833, 32493], [21635, 96663, 75027], [-29315, -130967, -101651]], [[10, 27, 18], [6, -11, -18], [-6, 27, 34]], [[28, 111, 84], [-12, -95, -84], [12, 111, 100]], [[266, 970, 705], [-10, -714, -705], [10, 970, 961]], [[1878, 4506, 2629], [2218, -410, -2629], [-2218, 4506, 6725]], [[253, 953, 701], [3, -697, -701], [-3, 953, 957]], [[1881, 4520, 2640], [2215, -424, -2640], [-2215, 4520, 6736]], [[233, 821, 589], [23, -565, -589], [-23, 821, 845]], [[1593, 3096, 1504], [2503, 1000, -1504], [-2503, 3096, 5600]], [[-7038, -35490, -28451], [-19586, -98654, -79069], [27266, 137310, 110045]], [[196, 695, 500], [60, -439, -500], [-60, 695, 756]], [[1590, 3082, 1493], [2506, 1014, -1493], [-2506, 3082, 5589]], [[166, 490, 325], [90, -234, -325], [-90, 490, 581]], [[149002, 670490, 521489], [375174, 1688246, 1313071], [-506214, -2277910, -1771695]], [[163, 546, 384], [93, -290, -384], [-93, 546, 640]], [[145, 457, 313], [111, -201, -313], [-111, 457, 569]], [[148969, 670341, 521373], [375207, 1688395, 1313187], [-506247, -2278059, -1771811]], [[178, 606, 429], [78, -350, -429], [-78, 606, 685]], [[9389, 42057, 32669], [21587, 96439, 74851], [-29267, -130743, -101475]], [[46, 195, 150], [-30, -179, -150], [30, 195, 166]], [[4, -1, -4], [12, 17, 4], [-12, -1, 12]], [[-7041, -35504, -28462], [-19583, -98640, -79058], [27263, 137296, 110034]], [[184, 579, 396], [72, -323, -396], [-72, 579, 652]], [[22, 83, 62], [-6, -67, -62], [6, 83, 78]], [[127, 368, 242], [129, -112, -242], [-129, 368, 498]], [[25, 97, 73], [-9, -81, -73], [9, 97, 89]], [[118, 289, 172], [138, -33, -172], [-138, 289, 428]], [[19, 69, 51], [-3, -53, -51], [3, 69, 67]], [[199, 639, 441], [57, -383, -441], [-57, 639, 697]], [[160, 517, 358], [96, -261, -358], [-96, 517, 614]]]
target = vector(ZZ,[84118752460105480846935836819753079271600697690686619664255230678276718877418958891792249030775786942317984652111184426018279427, 89173103422445447876715049689189652193176619520301916283899743110137112860432642548206151350732936688768966032976538813292605444, -132496067393083180057627771316425335059370948823049050270938486557240570794895542908205751446110117596540703704248469623120326662])

#part1 get padding
P = Matrix(ZZ,[[2, 9, 7], [1, 5, 4], [1, 1, 1]])
P_inv = Matrix(ZZ,[[1, -2, 1], [3, -5, -1], [-4, 7, 1]])
L = [P*Matrix(ZZ,i)*P_inv for i in matrices]
padding = []
for i in L:
    len1 = len(bin(i[0,0])[2:]) // 4
    len2 = len(bin(i[1,1])[2:]) // 4
    pad1 = hex(i[2,0])[2:].zfill(len1)
    pad2 = hex(i[2,1])[2:].zfill(len2)
    padding.append((pad1,pad2))
#print(padding)


#part2 c2,init
PR.<x> = PolynomialRing(ZZ)
a = vector([80+256*x,396+1280*x, 317+1024*x])
#print(a*P_inv)
final = P*target
c2 = hex(final[2])[2:]
#print(c2)


#part3 josephus to get flag
ls1 = [i for i in range(1,105+1)]
index = []
num = 0
while len(ls1) > 1:
    num +=1
    count = ls1.pop(0)
    if num == 2:
        index.append(count)
        num = 0
    else:
        ls1.append(count)
index.append(ls1[0])

c2 = c2[::-1]
flag = ["" for i in range(105)]
for i in range(105):
    flag[index[i]-1] = c2[i]
flag = "".join(flag)
print("TPCTF{",end = "")
for i in range(0,len(flag),7):
    temp = chr(int(flag[i:i+7],2))
    print(temp,end = "")
print("}")

#TPCTF{undec1dab1e_PcP}

确实是非常有创意的一道题目，惊叹于出题人绝妙的想法。