糖醋小鸡块的blog
0%

2023-强网拟态-wp-crypto

发表于 分类于 Valine：

*代表赛中未出题目。赛中一共做出两道，最后一道目前还没有进一步的思路，所以先阐述一下自己的想法，希望能给各位师傅一些启发。

一眼看出

题目描述：

1
一眼看穿

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from Crypto.Util.number import *
from secret import flag
import gmpy2


flag=b''

r = getPrime(6)

a = 11001240791308496565411773845509754352597481464288272699325231395472137144610774645372812149675141360600469640492874223541765389441131365669731006263464699

p = gmpy2.next_prime(a - r)
q = gmpy2.next_prime(gmpy2.next_prime(a) + r)

n = p*q

def enc(flag, n):
    m = bytes_to_long(flag)
    return pow(m, 65537, n)


c = enc(flag, n)
print('n =', n)
print('c =', c)

# ('n =', mpz(121027298948349995679677982412648544403333177260975245569073983061538581058440163574922807151182889153495253964764966037308461724272151584478723275142858008261257709817963330011376266261119767294949088397671360123321149414700981035517299807126625758046100840667081332434968770862731073693976604061597575813313L))
# ('c =', mpz(42256117129723577554705402387775886393426604555611637074394963219097781224776058009003521565944180241032100329456702310737369381890041336312084091995865560402681403775751012856436207938771611177592600423563671217656908392901713661029126149486651409531213711103407037959788587839729511719756709763927616470267L))

签到题，没有太多可说的东西。主要就是r只有六位，因此可以爆破求出n的分解。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from Crypto.Util.number import *
import gmpy2

n = 121027298948349995679677982412648544403333177260975245569073983061538581058440163574922807151182889153495253964764966037308461724272151584478723275142858008261257709817963330011376266261119767294949088397671360123321149414700981035517299807126625758046100840667081332434968770862731073693976604061597575813313
c = 42256117129723577554705402387775886393426604555611637074394963219097781224776058009003521565944180241032100329456702310737369381890041336312084091995865560402681403775751012856436207938771611177592600423563671217656908392901713661029126149486651409531213711103407037959788587839729511719756709763927616470267
a = 11001240791308496565411773845509754352597481464288272699325231395472137144610774645372812149675141360600469640492874223541765389441131365669731006263464699

for r in range(2**6):
    p = gmpy2.next_prime(a - r)
    q = gmpy2.next_prime(gmpy2.next_prime(a) + r)
    if(n % p == 0):
        d = inverse(65537,(p-1)*(q-1))
        print(long_to_bytes(pow(c,d,n)))
        exit()

#flag{621f7c4f-21de-8566-649e-5a883ce318dc}



almostlinear

题目描述：

1
我的Sbox不是线性的！原来随便调整一下就好了，那么用这样的Sbox就安全了……叭？

题目：

task.py：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
# !/usr/bin/env python
from Crypto.Util.number import *
from hashlib import sha256
from base64 import b64encode
import socketserver
import os
import sys
import random
import signal
import string
from random import *
from Crypto.Util.number import *
from myAES import myAES


class Task(socketserver.BaseRequestHandler):
    def _recvall(self):
        BUFF_SIZE = 2048
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline:
                msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self, prompt=b'> '):
        self.send(prompt, newline=False)
        return self._recvall()

    def close(self):
        self.request.close()

    def proof_of_work(self):
        seed(os.urandom(8))
        proof = ''.join(
            [choice(string.ascii_letters+string.digits) for _ in range(20)])
        _hexdigest = sha256(proof.encode()).hexdigest()
        self.send(f"[+] sha256(XXXX+{proof[4:]}) == {_hexdigest}".encode())
        x = self.recv(prompt=b'[+] Plz tell me XXXX: ')
        if len(x) != 4 or sha256(x+proof[4:].encode()).hexdigest() != _hexdigest:
            return False
        return True

    def chal(self):
        key = long_to_bytes(getrandbits(128)).rjust(16, b"\00")
        token = hex(getrandbits(64))[2:].zfill(16).encode()
        cipher = myAES(key)
        flag = cipher.encrypt(token)
        self.send(("flag: "+flag.hex()).encode())
        test = bytes.fromhex(self.recv(b"try: ")[:32].decode())
        ctx = cipher.encrypt(test)
        self.send(("your ans: "+ctx.hex()).encode())
        ans = self.recv(b"token: ")
        if token == ans:
            f=open("./flag","rb")
            FLAG=f.read()
            f.close()
            self.send(FLAG)
        else:
            self.send(b"wrong")

    def handle(self):
        try:
            if not self.proof_of_work():
                self.send(b"try again!")
                self.close()
                exit()
                
            for i in range(1000):
                self.chal()
        except:
            self.send(b"something wrong! plz try again!")
            self.close()


class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass


class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
    pass


if __name__ == "__main__":
    HOST, PORT = '0.0.0.0', 12345
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    server.serve_forever()

cons.py：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
from secret import sbox_linear
from hashlib import sha256
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
    
    
sbox_change = (
        0x13, 0x39, 0x47, 0x6d, 0xbb, 0x91, 0xef, 0xc5, 0x58, 0x72, 0x0c, 0x26, 0xf0, 0xda, 0xa4, 0x8e, 
        0x85, 0xaf, 0xd1, 0xfb, 0x2d, 0x07, 0x79, 0x53, 0xce, 0xe4, 0x9a, 0xb0, 0x66, 0x4c, 0x32, 0x18, 
        0x24, 0x0e, 0x70, 0x0a, 0x8c, 0xa6, 0x5a, 0xf2, 0x6f, 0x45, 0x3b, 0x11, 0xc7, 0xed, 0x93, 0xb9, 
        0xb2, 0x98, 0xe6, 0xcc, 0x1a, 0x30, 0x4e, 0x64, 0xf9, 0xd3, 0xad, 0x87, 0x51, 0x7b, 0x05, 0x2f, 
        0x7d, 0x57, 0x29, 0x03, 0xd5, 0xff, 0x81, 0xab, 0x36, 0x1c, 0x62, 0x48, 0x9e, 0xb4, 0xca, 0xe0, 
        0xeb, 0xc1, 0xbf, 0x95, 0x43, 0x69, 0x17, 0x3d, 0xa0, 0x8a, 0xf4, 0xde, 0x08, 0x22, 0x5c, 0x76, 
        0x4a, 0x60, 0x1e, 0x34, 0xe2, 0xc8, 0xb6, 0x9c, 0x01, 0x2b, 0x55, 0x7f, 0xa9, 0x83, 0xfd, 0xd7, 
        0xdc, 0xf6, 0x88, 0xa2, 0x74, 0x5e, 0x20, 0x15, 0x97, 0xbd, 0xc3, 0xe9, 0x3f, 0x59, 0x6b, 0x41, 
        0xcf, 0xe5, 0x9b, 0xb1, 0x67, 0x4d, 0x33, 0x19, 0x84, 0xae, 0xd0, 0xfa, 0x2c, 0x06, 0x78, 0x52, 
        0xd8, 0x73, 0x0d, 0x27, 0xf1, 0xdb, 0xa5, 0x8f, 0x12, 0x38, 0x46, 0x6c, 0xba, 0x90, 0xee, 0xc4, 
        0xf8, 0xd2, 0xac, 0x86, 0x50, 0x7a, 0x04, 0x2e, 0xb3, 0x99, 0xe7, 0xcd, 0x1b, 0x31, 0x4f, 0x65, 
        0x6e, 0x44, 0x3a, 0x10, 0xc6, 0xec, 0x92, 0xb8, 0x25, 0x0f, 0x71, 0x5b, 0x8d, 0xa7, 0xd9, 0xf3, 
        0xa1, 0x8b, 0xf5, 0xdf, 0x09, 0x23, 0x5d, 0x77, 0xea, 0xc0, 0xbe, 0x94, 0x42, 0x68, 0x16, 0x3c, 
        0x37, 0x1d, 0x63, 0x49, 0x9f, 0xb5, 0xcb, 0xe1, 0x7c, 0x56, 0x28, 0x02, 0xd4, 0xfe, 0x80, 0xaa, 
        0x96, 0xbc, 0xc2, 0xe8, 0x3e, 0x14, 0x6a, 0x40, 0xdd, 0xf7, 0x89, 0xa3, 0x75, 0x5f, 0x21, 0x0b, 
        0x00, 0x2a, 0x54, 0x7e, 0xa8, 0x82, 0xfc, 0xd6, 0x4b, 0x61, 0x1f, 0x35, 0xe3, 0xc9, 0xb7, 0x9d
)

rcon = (0x8d, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36)

gmul2 = (
        0x00, 0x02, 0x04, 0x06, 0x08, 0x0a, 0x0c, 0x0e, 0x10, 0x12, 0x14, 0x16, 0x18, 0x1a, 0x1c, 0x1e, 
        0x20, 0x22, 0x24, 0x26, 0x28, 0x2a, 0x2c, 0x2e, 0x30, 0x32, 0x34, 0x36, 0x38, 0x3a, 0x3c, 0x3e, 
        0x40, 0x42, 0x44, 0x46, 0x48, 0x4a, 0x4c, 0x4e, 0x50, 0x52, 0x54, 0x56, 0x58, 0x5a, 0x5c, 0x5e, 
        0x60, 0x62, 0x64, 0x66, 0x68, 0x6a, 0x6c, 0x6e, 0x70, 0x72, 0x74, 0x76, 0x78, 0x7a, 0x7c, 0x7e, 
        0x80, 0x82, 0x84, 0x86, 0x88, 0x8a, 0x8c, 0x8e, 0x90, 0x92, 0x94, 0x96, 0x98, 0x9a, 0x9c, 0x9e, 
        0xa0, 0xa2, 0xa4, 0xa6, 0xa8, 0xaa, 0xac, 0xae, 0xb0, 0xb2, 0xb4, 0xb6, 0xb8, 0xba, 0xbc, 0xbe, 
        0xc0, 0xc2, 0xc4, 0xc6, 0xc8, 0xca, 0xcc, 0xce, 0xd0, 0xd2, 0xd4, 0xd6, 0xd8, 0xda, 0xdc, 0xde, 
        0xe0, 0xe2, 0xe4, 0xe6, 0xe8, 0xea, 0xec, 0xee, 0xf0, 0xf2, 0xf4, 0xf6, 0xf8, 0xfa, 0xfc, 0xfe, 
        0x1b, 0x19, 0x1f, 0x1d, 0x13, 0x11, 0x17, 0x15, 0x0b, 0x09, 0x0f, 0x0d, 0x03, 0x01, 0x07, 0x05, 
        0x3b, 0x39, 0x3f, 0x3d, 0x33, 0x31, 0x37, 0x35, 0x2b, 0x29, 0x2f, 0x2d, 0x23, 0x21, 0x27, 0x25, 
        0x5b, 0x59, 0x5f, 0x5d, 0x53, 0x51, 0x57, 0x55, 0x4b, 0x49, 0x4f, 0x4d, 0x43, 0x41, 0x47, 0x45, 
        0x7b, 0x79, 0x7f, 0x7d, 0x73, 0x71, 0x77, 0x75, 0x6b, 0x69, 0x6f, 0x6d, 0x63, 0x61, 0x67, 0x65, 
        0x9b, 0x99, 0x9f, 0x9d, 0x93, 0x91, 0x97, 0x95, 0x8b, 0x89, 0x8f, 0x8d, 0x83, 0x81, 0x87, 0x85, 
        0xbb, 0xb9, 0xbf, 0xbd, 0xb3, 0xb1, 0xb7, 0xb5, 0xab, 0xa9, 0xaf, 0xad, 0xa3, 0xa1, 0xa7, 0xa5, 
        0xdb, 0xd9, 0xdf, 0xdd, 0xd3, 0xd1, 0xd7, 0xd5, 0xcb, 0xc9, 0xcf, 0xcd, 0xc3, 0xc1, 0xc7, 0xc5, 
        0xfb, 0xf9, 0xff, 0xfd, 0xf3, 0xf1, 0xf7, 0xf5, 0xeb, 0xe9, 0xef, 0xed, 0xe3, 0xe1, 0xe7, 0xe5
    )

gmul3 = (
        0x00, 0x03, 0x06, 0x05, 0x0c, 0x0f, 0x0a, 0x09, 0x18, 0x1b, 0x1e, 0x1d, 0x14, 0x17, 0x12, 0x11, 
        0x30, 0x33, 0x36, 0x35, 0x3c, 0x3f, 0x3a, 0x39, 0x28, 0x2b, 0x2e, 0x2d, 0x24, 0x27, 0x22, 0x21, 
        0x60, 0x63, 0x66, 0x65, 0x6c, 0x6f, 0x6a, 0x69, 0x78, 0x7b, 0x7e, 0x7d, 0x74, 0x77, 0x72, 0x71, 
        0x50, 0x53, 0x56, 0x55, 0x5c, 0x5f, 0x5a, 0x59, 0x48, 0x4b, 0x4e, 0x4d, 0x44, 0x47, 0x42, 0x41, 
        0xc0, 0xc3, 0xc6, 0xc5, 0xcc, 0xcf, 0xca, 0xc9, 0xd8, 0xdb, 0xde, 0xdd, 0xd4, 0xd7, 0xd2, 0xd1, 
        0xf0, 0xf3, 0xf6, 0xf5, 0xfc, 0xff, 0xfa, 0xf9, 0xe8, 0xeb, 0xee, 0xed, 0xe4, 0xe7, 0xe2, 0xe1, 
        0xa0, 0xa3, 0xa6, 0xa5, 0xac, 0xaf, 0xaa, 0xa9, 0xb8, 0xbb, 0xbe, 0xbd, 0xb4, 0xb7, 0xb2, 0xb1, 
        0x90, 0x93, 0x96, 0x95, 0x9c, 0x9f, 0x9a, 0x99, 0x88, 0x8b, 0x8e, 0x8d, 0x84, 0x87, 0x82, 0x81, 
        0x9b, 0x98, 0x9d, 0x9e, 0x97, 0x94, 0x91, 0x92, 0x83, 0x80, 0x85, 0x86, 0x8f, 0x8c, 0x89, 0x8a, 
        0xab, 0xa8, 0xad, 0xae, 0xa7, 0xa4, 0xa1, 0xa2, 0xb3, 0xb0, 0xb5, 0xb6, 0xbf, 0xbc, 0xb9, 0xba, 
        0xfb, 0xf8, 0xfd, 0xfe, 0xf7, 0xf4, 0xf1, 0xf2, 0xe3, 0xe0, 0xe5, 0xe6, 0xef, 0xec, 0xe9, 0xea, 
        0xcb, 0xc8, 0xcd, 0xce, 0xc7, 0xc4, 0xc1, 0xc2, 0xd3, 0xd0, 0xd5, 0xd6, 0xdf, 0xdc, 0xd9, 0xda, 
        0x5b, 0x58, 0x5d, 0x5e, 0x57, 0x54, 0x51, 0x52, 0x43, 0x40, 0x45, 0x46, 0x4f, 0x4c, 0x49, 0x4a, 
        0x6b, 0x68, 0x6d, 0x6e, 0x67, 0x64, 0x61, 0x62, 0x73, 0x70, 0x75, 0x76, 0x7f, 0x7c, 0x79, 0x7a, 
        0x3b, 0x38, 0x3d, 0x3e, 0x37, 0x34, 0x31, 0x32, 0x23, 0x20, 0x25, 0x26, 0x2f, 0x2c, 0x29, 0x2a, 
        0x0b, 0x08, 0x0d, 0x0e, 0x07, 0x04, 0x01, 0x02, 0x13, 0x10, 0x15, 0x16, 0x1f, 0x1c, 0x19, 0x1a
    )


if __name__=="__main__":
    assert(5<=sum([i^j for i,j in zip(sbox_change,sbox_linear)])<0x500)
    assert(5<=sum([(i-j)&0xff for i,j in zip(sbox_change,sbox_linear)])<0x500)
    key=sha256(bytes(sbox_linear)).digest()
    f=open("hint.py","rb")
    hints=f.read()
    f.close()
    cipher=AES.new(key,AES.MODE_ECB)
    hints_enc=cipher.encrypt(pad(hints,16))
    f=open("hint.py.enc","wb")
    f.write(hints_enc)
    f.close()

还有一个AES的具体实现，和加密后的hint，需要全部附件的师傅可以找我要。

这个题抢到一个一血，值得纪念。回到题目，还是简单分析一下题目任务：

  • 通过proof
  • 随机生成16字节的AES密钥，并随机生成一个十六字节且每个字节都是十六进制数的token
  • 首先给出用他的AES加密后的token
  • 然后，我们可以输入一段值，并获得这段值用他的AES加密的结果
  • 最后我们需要用这些信息解出token值并传回给他，token正确就能得到flag
  • 有一个需要额外注意的点，就是每一次连接靶机有一千次机会可以传回token，正确一次就可以得到flag。所以解决这题应该是个概率性的问题

那么首先观察他的AES究竟做了一些什么变化，测试出来其实就是S盒改变了而已。结合题目提示，这个S盒肯定有不安全的地方。这一部分让我想到前一段时间做的羊城杯决赛的newAES一题，于是我先分析一下这个S盒的抗差分性质，然后发现果然这个S盒的抗差分性质非常差。

对于S盒的差分分析不太清楚的可以看看我写的这篇：

Crypto趣题-分组密码 | 糖醋小鸡块的blog (tangcuxiaojikuai.xyz)

但是，newAES那个题目中，他的S盒是完全差分可逆的，但是这一题的S盒只是抗差分性质较差，并不完全可逆。这里我具体列举一下差分分布表的其中一行让大家可以看出区别：

正常S盒：

1
[0, 2, 0, 0, 2, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 0, 2, 2, 0, 0, 2, 2, 2, 0, 0, 0, 2, 4, 0, 2, 2, 0, 2, 0, 0, 0, 0, 2, 2, 0, 0, 2, 0, 2, 2, 2, 0, 0, 0, 2, 2, 2, 2, 2, 2, 2, 0, 0, 0, 2, 0, 0, 0, 2, 0, 0, 0, 2, 2, 0, 2, 2, 2, 0, 2, 2, 0, 2, 0, 2, 2, 0, 0, 0, 2, 2, 2, 0, 0, 0, 0, 0, 0, 0, 2, 2, 0, 2, 0, 0, 0, 2, 2, 2, 2, 0, 2, 0, 0, 0, 2, 0, 0, 2, 0, 0, 2, 2, 0, 0, 0, 2, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 0, 2, 2, 0, 0, 0, 2, 0, 0, 2, 0, 2, 0, 0, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 0, 2, 0, 2, 2, 2, 2, 2, 2, 0, 0, 2, 0, 2, 0, 2, 2, 2, 2, 0, 0, 2, 0, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 0, 2, 2, 0, 0, 0, 0, 2, 0, 0, 0, 2, 2, 0, 0, 2, 2, 0, 0, 2, 0, 0, 2, 0, 0, 2, 0, 0, 2, 2, 2, 0, 0, 2, 0, 0, 0, 2, 2, 2, 0, 2, 2, 0, 0, 0, 2]

羊城杯那题S盒的差分分布：

1
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 256, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

本题S盒的差分分布：

1
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 246, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

对于完全差分可逆的S盒(如羊城杯那题的S盒)，我们拥有输入的值的密文以及token的密文，所以就有密文差分，然后由于差分可逆，就可以逐步将差分逆回去得到明文差分，然后将明文差分与我们的输入值异或，就得到了token。

而本题S盒虽然并不是完全差分可逆的，但是可以观察到，他的差分分布仍然极不均匀，一个明文差分在经历S盒后，大部分会集中在另一个差分。因此，我们可以把这个集中分布的差分视作是差分可逆的，去求解我们的密文差分。而只要我们随机到一个token，使其与我们的输入密文满足AES中所有差分均对应在这个集中分布的差分上，就可以解出token。因此解法是概率性的，具体的概率我简单想了一下，应该是这样计算：记AES中用到差分S盒的次数为n，那么成功概率应该是：

理论上来说非常低，但是既然提供了多次交互次数，那么由生日攻击的原理知道，我们交互多次就有大概率得到一组满足题意的解。

这就是我的做法，我赛中连接几十次靶机就随机到了一组满足条件的token值，进而获得flag。这个解法也并没有用到题目的hint，所以可能有其他进一步的优化方法可以提高这个概率，使其能在一次连接靶机内就随机出能解的token。(因为并没有具体计算这个概率为多大，所以也可能是运气非常好，才能在几十次内得到解)

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
from Crypto.Util.number import *
from pwn import *
from tqdm import *
from hashlib import sha256
from random import *

def xor(a,b):
    return bytes([i^j for i,j in zip(a,b)])

xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)

Rcon = (
    0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,
    0x80, 0x1B, 0x36, 0x6C, 0xD8, 0xAB, 0x4D, 0x9A,
    0x2F, 0x5E, 0xBC, 0x63, 0xC6, 0x97, 0x35, 0x6A,
    0xD4, 0xB3, 0x7D, 0xFA, 0xEF, 0xC5, 0x91, 0x39,
)


def text2matrix(text):
    text = int(text.hex(), 16)
    matrix = []
    for i in range(16):
        byte = (text >> (8 * (15 - i))) & 0xFF
        if i % 4 == 0:
            matrix.append([byte])
        else:
            matrix[i // 4].append(byte)
    return matrix


def matrix2text(matrix):
    text = 0
    for i in range(4):
        for j in range(4):
            text |= (matrix[i][j] << (120 - 8 * (4 * i + j)))
    return text.to_bytes(16, byteorder='big')


class AES:
    def __init__(self, Sbox):
        self.Sbox = Sbox
        self.InvSbox = [0]* 256
        for i in range(256):
            self.InvSbox[self.Sbox[i]] = i

    def decrypt(self, ciphertext):
        self.cipher_state = text2matrix(ciphertext)
        self.__inv_shift_rows(self.cipher_state)
        self.__inv_sub_bytes(self.cipher_state)

        for i in range(9, 0, -1):
            self.__round_decrypt(self.cipher_state)

        return matrix2text(self.cipher_state)

    def __round_decrypt(self, state_matrix):
        self.__inv_mix_columns(state_matrix)
        self.__inv_shift_rows(state_matrix)
        self.__inv_sub_bytes(state_matrix)

    def __inv_sub_bytes(self, s):
        for i in range(4):
            for j in range(4):
                s[i][j] = self.InvSbox[s[i][j]]

    def __inv_shift_rows(self, s):
        s[0][1], s[1][1], s[2][1], s[3][1] = s[3][1], s[0][1], s[1][1], s[2][1]
        s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
        s[0][3], s[1][3], s[2][3], s[3][3] = s[1][3], s[2][3], s[3][3], s[0][3]

    def __mix_single_column(self, a):
        t = a[0] ^ a[1] ^ a[2] ^ a[3]
        u = a[0]
        a[0] ^= t ^ xtime(a[0] ^ a[1])
        a[1] ^= t ^ xtime(a[1] ^ a[2])
        a[2] ^= t ^ xtime(a[2] ^ a[3])
        a[3] ^= t ^ xtime(a[3] ^ u)


    def __mix_columns(self, s):
        for i in range(4):
            self.__mix_single_column(s[i])


    def __inv_mix_columns(self, s):
        for i in range(4):
            u = xtime(xtime(s[i][0] ^ s[i][2]))
            v = xtime(xtime(s[i][1] ^ s[i][3]))
            s[i][0] ^= u
            s[i][1] ^= v
            s[i][2] ^= u
            s[i][3] ^= v

        self.__mix_columns(s)

def get_sbox_diff(sbox):          
    t = [[0 for i in range(256)] for j in range(256)]
    for i in range(256):
        for j in range(256):
            t[i^j][sbox[i]^sbox[j]] += 1

    sbox_diff = [0 for i in range(256)]

    for i in range(256):
        for j in range(256):
            if t[i][j] == 246:
                sbox_diff[i] = j
    return sbox_diff

sbox = (
        0x13, 0x39, 0x47, 0x6d, 0xbb, 0x91, 0xef, 0xc5, 0x58, 0x72, 0x0c, 0x26, 0xf0, 0xda, 0xa4, 0x8e, 
        0x85, 0xaf, 0xd1, 0xfb, 0x2d, 0x07, 0x79, 0x53, 0xce, 0xe4, 0x9a, 0xb0, 0x66, 0x4c, 0x32, 0x18, 
        0x24, 0x0e, 0x70, 0x0a, 0x8c, 0xa6, 0x5a, 0xf2, 0x6f, 0x45, 0x3b, 0x11, 0xc7, 0xed, 0x93, 0xb9, 
        0xb2, 0x98, 0xe6, 0xcc, 0x1a, 0x30, 0x4e, 0x64, 0xf9, 0xd3, 0xad, 0x87, 0x51, 0x7b, 0x05, 0x2f, 
        0x7d, 0x57, 0x29, 0x03, 0xd5, 0xff, 0x81, 0xab, 0x36, 0x1c, 0x62, 0x48, 0x9e, 0xb4, 0xca, 0xe0, 
        0xeb, 0xc1, 0xbf, 0x95, 0x43, 0x69, 0x17, 0x3d, 0xa0, 0x8a, 0xf4, 0xde, 0x08, 0x22, 0x5c, 0x76, 
        0x4a, 0x60, 0x1e, 0x34, 0xe2, 0xc8, 0xb6, 0x9c, 0x01, 0x2b, 0x55, 0x7f, 0xa9, 0x83, 0xfd, 0xd7, 
        0xdc, 0xf6, 0x88, 0xa2, 0x74, 0x5e, 0x20, 0x15, 0x97, 0xbd, 0xc3, 0xe9, 0x3f, 0x59, 0x6b, 0x41, 
        0xcf, 0xe5, 0x9b, 0xb1, 0x67, 0x4d, 0x33, 0x19, 0x84, 0xae, 0xd0, 0xfa, 0x2c, 0x06, 0x78, 0x52, 
        0xd8, 0x73, 0x0d, 0x27, 0xf1, 0xdb, 0xa5, 0x8f, 0x12, 0x38, 0x46, 0x6c, 0xba, 0x90, 0xee, 0xc4, 
        0xf8, 0xd2, 0xac, 0x86, 0x50, 0x7a, 0x04, 0x2e, 0xb3, 0x99, 0xe7, 0xcd, 0x1b, 0x31, 0x4f, 0x65, 
        0x6e, 0x44, 0x3a, 0x10, 0xc6, 0xec, 0x92, 0xb8, 0x25, 0x0f, 0x71, 0x5b, 0x8d, 0xa7, 0xd9, 0xf3, 
        0xa1, 0x8b, 0xf5, 0xdf, 0x09, 0x23, 0x5d, 0x77, 0xea, 0xc0, 0xbe, 0x94, 0x42, 0x68, 0x16, 0x3c, 
        0x37, 0x1d, 0x63, 0x49, 0x9f, 0xb5, 0xcb, 0xe1, 0x7c, 0x56, 0x28, 0x02, 0xd4, 0xfe, 0x80, 0xaa, 
        0x96, 0xbc, 0xc2, 0xe8, 0x3e, 0x14, 0x6a, 0x40, 0xdd, 0xf7, 0x89, 0xa3, 0x75, 0x5f, 0x21, 0x0b, 
        0x00, 0x2a, 0x54, 0x7e, 0xa8, 0x82, 0xfc, 0xd6, 0x4b, 0x61, 0x1f, 0x35, 0xe3, 0xc9, 0xb7, 0x9d
)




#part1 
def proof_of_work():
	table = string.digits + string.ascii_letters
	temp = r.recvuntil(b"sha256(XXXX+")
	temp = r.recvline()
	suffix = temp[:16].decode()
	hex1 = temp[20:].strip().decode()
	for i in tqdm(table):
		for j in table:
			for k in table:
				for m in table:
					temp1 = i+j+k+m
					if(sha256((temp1+suffix).encode()).hexdigest() == hex1):
						r.sendline(temp1.encode())
						return
aes = AES(Sbox=get_sbox_diff(sbox))

while(1):
    r = remote("pwn-8ffbe21dcb.challenge.xctf.org.cn", 9999, ssl=True)
    proof_of_work()


    for i in trange(1000):
        r.recvuntil(b"flag: ")
        c1 = r.recvline().strip().decode()
        #print(c1)
        r.recvuntil(b"try: ")

        m2 = b"\x00"*16
        r.sendline(b"0"*32)
        r.recvuntil(b"your ans: ")
        c2 = r.recvline().strip().decode()
        #print(c2)
        r.recvuntil(b"token: ")

        c1 = long_to_bytes(int(c1,16))
        c2 = long_to_bytes(int(c2,16))

        diff1 = xor(c1,c2)
        temp1 = aes.decrypt(diff1)
        t = xor(temp1,m2)
        #print(t)
        r.sendline(t)

        temp = r.recvline()
        if(b"wrong" not in temp):
            print(temp)
            exit()
    r.close()

#flag{vnJnqLauu29C0nBEJ9FVgWkeyNR2meC4}



*doublecheck

题目描述：

1
我的加密机不知道为什么莫名其妙坏了，输出的密文好像总是有些问题……不过既然如此，那我就有了一个新的加密机，一起使用的话，满足同时绕过两个加密机可就难喽~

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
# !/usr/bin/env python
from Crypto.Util.number import *
from hashlib import sha256
import socketserver
import signal
import string
from os import popen, urandom
from Crypto.Util.number import *
from random import *


class Task(socketserver.BaseRequestHandler):
    def _recvall(self):
        BUFF_SIZE = 2048
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline:
                msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self, prompt=b'> '):
        self.send(prompt, newline=False)
        return self._recvall()

    def close(self):
        self.request.close()

    def proof_of_work(self):
        seed(urandom(8))
        proof = ''.join(
            [choice(string.ascii_letters+string.digits) for _ in range(20)])
        _hexdigest = sha256(proof.encode()).hexdigest()
        self.send(f"[+] sha256(XXXX+{proof[4:]}) == {_hexdigest}".encode())
        x = self.recv(prompt=b'[+] Plz tell me XXXX: ')
        if len(x) != 4 or sha256(x+proof[4:].encode()).hexdigest() != _hexdigest:
            return False
        return True

    def handle(self):
        try:
            if not self.proof_of_work():
                self.send(b"try again!")
                self.close()
                exit()

            key = hex(getrandbits(128))[2:].rjust(32, "0")

            pts = hex(getrandbits(64))[2:].rjust(16, "0")
            ptsh = pts.encode().hex()

            cts1 = popen("./cipher "+key+" "+ptsh).read()[:-1].encode()
            cts2 = popen("./cipher_broken "+key+" "+ptsh).read()[:-1].encode()
            self.send(b"T: "+cts1)
            self.send(b"F: "+cts2)
            signal.alarm(10)

            ans = self.recv()

            if ans == pts.encode():
                f=open("./flag","rb")
                FLAG=f.read()
                f.close()
                self.send(FLAG)
            else:
                self.send(b"sorry,plz try again")
        except:
            self.send(b"something wrong! plz try again!")
            self.close()


class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass


class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
    pass


if __name__ == "__main__":
    HOST, PORT = '0.0.0.0', 12345
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    server.serve_forever()

题目任务挺简单的，总结一下就是：

  • 通过proof
  • 随机生成16字节的key，并随机生成一个十六字节且每个字节都是十六进制数的pts
  • 将pts分别用cipher、cipher_broken进行加密，并给出两个密文
  • 传给靶机pts，如果正确则得到flag

那么核心任务就是找到两个加密文件的区别，并找出这个区别会对密文分别造成什么影响，然后用这个泄露信息去解密。

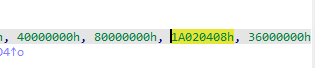
拖进IDA里看看加密过程，发现两个cipher其实都是标准AES加密，代码部分没有任何不同。那么应该也是改变了AES中的某个常量，进一步就会发现，cipher_broken的密钥扩展中的轮常量的倒数第二个值发生了变化。

正常的是：

image-20231112102552264

broken的是：

image-20231112102541006

那么就要通过这个区别来想办法解AES。然后我的思路如下(看不太明白的师傅可以熟悉一下AES的加密流程)：

尝试

我的思路主要是利用第十轮解密以及第十轮密钥扩展来对第十轮密钥进行逐字节爆破：

利用第十轮解密

由于第九轮轮常量有区别，因此密钥扩展算法后的第九轮和第十轮轮密钥会受到影响。换一个角度，这也就是说在进行第九轮的轮密钥加之前，两个AES加密得到的结果都是完全一样的，也就是下图中，红线部分的值对于两个AES都相同，在第九轮轮密钥加之后开始产生区别：

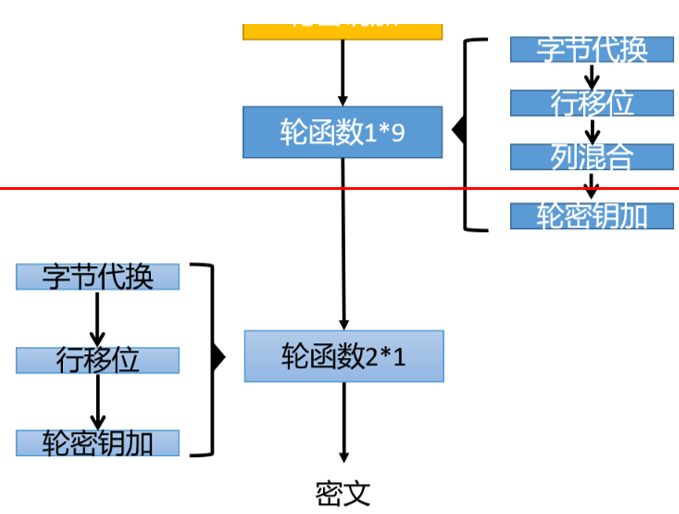
image-20231112102949899

而由于第九轮轮常量的不同，两个AES的第九轮轮密钥会产生如下的区别(左为正常AES第九轮轮密钥，右为broken的第九轮轮密钥)：

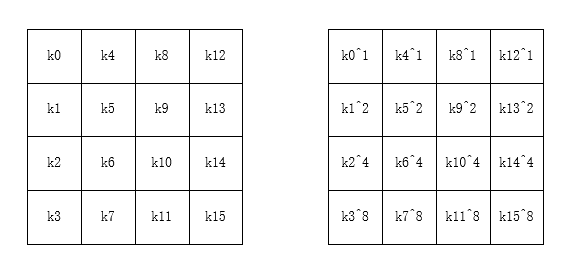
image-20231112103533388

而现在我们拥有密文，我们可以用中间相遇攻击的类似思路来逐字节爆破第十轮轮密钥，然后有了完整的第十轮轮密钥的话就可以用AES子密钥泄漏来反推所有密钥，进而解得AES明文。逐字节爆破的思路如下，这里我以第一次爆破为例：

  • 爆破正常第十轮轮密钥的第一个字节，和broken第十轮轮密钥的第一个字节
  • 将两个密文的第一个字节经过第十轮的逆轮密钥加->逆行移位->逆字节代换后，得到两个第九轮的轮密钥加之后的值，也就是下图黄线处的值：

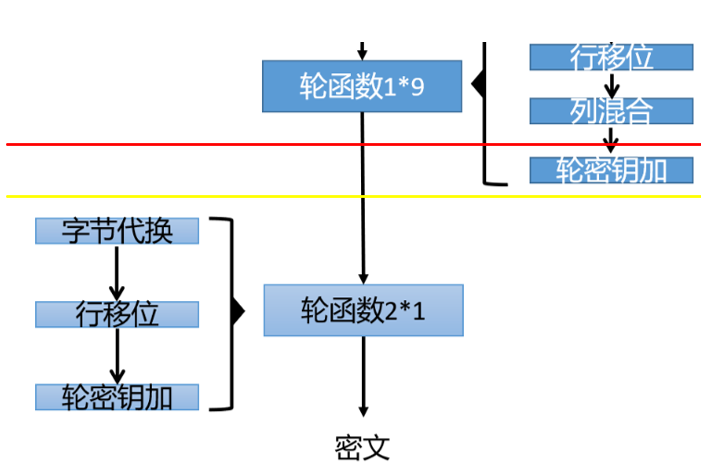
image-20231112104102983

  • 然后，由于两个AES的第九轮轮密钥差分是固定的，因此两个密文的差分应该也是固定的。比如对于第一个字节来说，黄线处的值差分应该等于1
  • 满足上面条件的就是可能的第十轮轮密钥的第一个字节

这样爆破完后，会发现每一个密钥仍然有256种可能性(注意一次其实是爆破两个字节，所以这里将可能性由2^16降到了2^8，确实是有效果的)。这里要注意：轮密钥有多种可能性是可以接受的，因为我们可以检查解出的密文是不是每个字节均是16进制字符。但是，显然这里的可能性还是太多了。因此还要想办法再降。

利用第十轮密钥扩展

然后下一步我的做法就是利用密钥扩展算法：

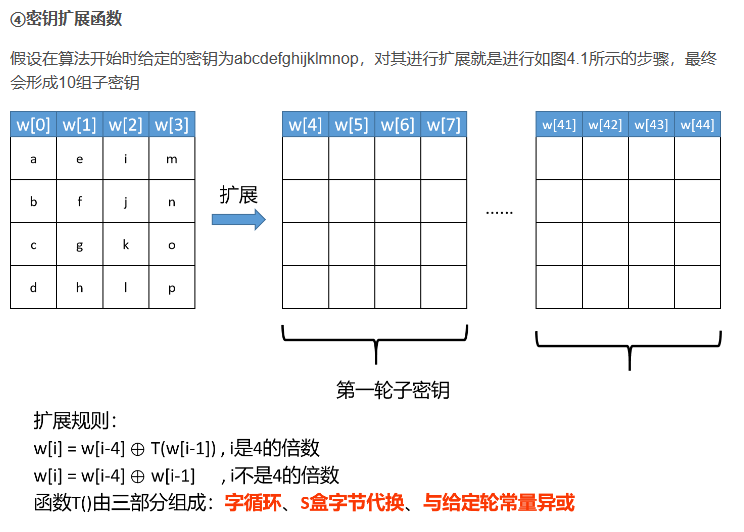
image-20231112104654806

也就是，我们将上一步的第十轮轮密钥的所有可能值爆破完后，继续逐字节爆破第九轮轮密钥的每个字节，并检查密钥扩展得到的两个第十轮密钥的这个字节是否在刚才得到的所有可能性里，如果不在的话，就可以从第十轮密钥的可能值中剔除掉，并且这一步是可以反复做的。经过测试发现，这样最多五轮后就无法再降低可能性，第十轮轮密钥的每个字节降低到了六十对左右(要记得这里本来是2^16对，到这里已经降低了很多)。

但是复杂度依然是不可接受的，我们还需要进一步减少第十轮轮密钥的可能性，但是我就没有想到进一步的做法了。

爆破脚本的本地实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
from Crypto.Util.number import *
from tqdm import *
import os
from AES_T import AES_T
from AES_F import AES_F

s_box = (
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)
inv_sbox = [0 for i in range(256)]
for i in range(256):
    inv_sbox[s_box[i]] = i

key = bytes_to_long(os.urandom(16))
plaintext = b"flagflagflagflag"
#T
aes = AES_T()
RoundKeys1 = aes.round_key_generator(key)
cipher_T = aes.aes_encrypt(plaintext, RoundKeys1)


#F
aes = AES_F()
RoundKeys2 = aes.round_key_generator(key)
cipher_F = aes.aes_encrypt(plaintext, RoundKeys2)

#逐字节爆破两个AES的第十轮轮密钥
key_10_dic = [[] for i in range(16)]
for i in range(16):
    for j in range(2**16):
        key10_1 = j&0xff
        key10_2 = j>>8
        cT = cipher_T[i]
        cF = cipher_F[i]
        cT ^= key10_1
        cF ^= key10_2
        #行移位可以不管，因为都在同一行，差分相同
        cT = inv_sbox[cT]
        cF = inv_sbox[cF]

        table = [1,2,4,8]
        if(cT == cF ^ table[i%4]):
            key_10_dic[i].append((key10_1,key10_2))

#check
if(0):
    for i in range(len(key_10_dic)):
        print((RoundKeys1[-1][i],RoundKeys2[-1][i]) in key_10_dic[i])


#反复去重
key9 = [[i for i in range(256)] for j in range(4)]
key9_ = [[] for i in range(4)]
for op in trange(5):
    ti = [[] for i in range(16)]
    if(op >= 1):
        key9 = key9_
        key9_ = [[] for i in range(4)]
    #第九轮密钥的前四个，有T函数
    for i in range(4):
        for j in key9[i]:
            key9_1 = int(j)
            table1 = [0x36,0,0,0]
            table2 = [2,4,8,1]
            table3 = [1,2,4,8]
            for k in key_10_dic[i]:
                temp1 = k[0]
                temp2 = k[1]
                key9_13_1 = inv_sbox[temp1 ^ key9_1 ^ table1[i%4]]
                key9_13_2 = inv_sbox[temp2 ^ (key9_1^table3[i%4]) ^ table1[i%4]]
                if(key9_13_1 == (key9_13_2^table2[i])):
                    ti[i].append((temp1,temp2))
                    key9_[i].append(key9_1)

    #第九轮密钥的后十二个，无T函数
    for i in range(4,16):
        for j in range(2**16):
            key9_1 = j&0xff
            key9_13 = j>>8
            key_10_1 = key9_1 ^ key9_13
            for k in key_10_dic[i-4]:
                if(k[0] == key9_13):
                    temp = k[1]
                    break
            table = [1,2,4,8]
            key_10_2 = (key9_1^table[i%4]) ^ temp
            if((key_10_1,key_10_2) in key_10_dic[i]):
                ti[i].append((key_10_1,key_10_2))


    ti = [set(ti[i]) for i in range(16)]
    print(len(ti[0]))

    #check
    if(1):
        for i in range(len(ti)):
            if((RoundKeys1[-1][i],RoundKeys2[-1][i]) in ti[i]):
                print(i,end = " ")
    key_10_dic = ti

然后其中的AES_F，AES_T是我从网上找的一个可以修改AES中任意常量的加密脚本，两者的区别也就只有轮密钥，所以在这里仅列出AES_T：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
class AES_T:

    MIX_C  = [[0x2, 0x3, 0x1, 0x1], [0x1, 0x2, 0x3, 0x1], [0x1, 0x1, 0x2, 0x3], [0x3, 0x1, 0x1, 0x2]]
    I_MIXC = [[0xe, 0xb, 0xd, 0x9], [0x9, 0xe, 0xb, 0xd], [0xd, 0x9, 0xe, 0xb], [0xb, 0xd, 0x9, 0xe]]
    RCon   = [0x01000000, 0x02000000, 0x04000000, 0x08000000, 0x10000000, 0x20000000, 0x40000000, 0x80000000, 0x1B000000, 0x36000000]

    S_BOX = [[0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76],
             [0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0],
             [0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15],
             [0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75],
             [0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84],
             [0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF],
             [0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8],
             [0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2],
             [0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73],
             [0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB],
             [0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79],
             [0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08],
             [0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A],
             [0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E],
             [0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF],
             [0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16]]

    I_SBOX = [[0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB],
              [0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB],
              [0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E],
              [0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25],
              [0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92],
              [0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84],
              [0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06],
              [0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B],
              [0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73],
              [0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E],
              [0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B],
              [0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4],
              [0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F],
              [0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF],
              [0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61],
              [0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D]]

    def SubBytes(self, State):
        # 字节替换
        return [self.S_BOX[i][j] for i, j in 
               [(_ >> 4, _ & 0xF) for _ in State]]

    def SubBytes_Inv(self, State):
        # 字节逆替换
        return [self.I_SBOX[i][j] for i, j in
               [(_ >> 4, _ & 0xF) for _ in State]]

    def ShiftRows(self, S):
        # 行移位
        return [S[ 0], S[ 5], S[10], S[15], 
                S[ 4], S[ 9], S[14], S[ 3],
                S[ 8], S[13], S[ 2], S[ 7],
                S[12], S[ 1], S[ 6], S[11]]

    def ShiftRows_Inv(self, S):
        # 逆行移位
        return [S[ 0], S[13], S[10], S[ 7],
                S[ 4], S[ 1], S[14], S[11],
                S[ 8], S[ 5], S[ 2], S[15],
                S[12], S[ 9], S[ 6], S[ 3]]

    def MixColumns(self, State):
        # 列混合
        return self.Matrix_Mul(self.MIX_C, State)

    def MixColumns_Inv(self, State):
        # 逆列混合
        return self.Matrix_Mul(self.I_MIXC, State)

    def RotWord(self, _4byte_block):
        # 用于生成轮密钥的字移位
        return ((_4byte_block & 0xffffff) << 8) + (_4byte_block >> 24)

    def SubWord(self, _4byte_block):
        # 用于生成密钥的字节替换
        result = 0
        for position in range(4):
            i = _4byte_block >> position * 8 + 4 & 0xf
            j = _4byte_block >> position * 8 & 0xf
            result ^= self.S_BOX[i][j] << position * 8
        return result

    def mod(self, poly, mod = 0b100011011):  
        # poly模多项式mod
        while poly.bit_length() > 8:
            poly ^= mod << poly.bit_length() - 9
        return poly

    def mul(self, poly1, poly2):
        # 多项式相乘
        result = 0
        for index in range(poly2.bit_length()):
            if poly2 & 1 << index:
                result ^= poly1 << index
        return result

    def Matrix_Mul(self, M1, M2):  # M1 = MIX_C  M2 = State
        # 用于列混合的矩阵相乘
        M = [0] * 16
        for row in range(4):
            for col in range(4):
                for Round in range(4):
                    M[row + col*4] ^= self.mul(M1[row][Round], M2[Round+col*4])
                M[row + col*4] = self.mod(M[row + col*4])
        return M

    def round_key_generator(self, _16bytes_key):
        # 轮密钥产生
        w = [_16bytes_key >> 96, 
             _16bytes_key >> 64 & 0xFFFFFFFF, 
             _16bytes_key >> 32 & 0xFFFFFFFF, 
             _16bytes_key & 0xFFFFFFFF] + [0]*40
        for i in range(4, 44):
            temp = w[i-1]
            if not i % 4:
                temp = self.SubWord(self.RotWord(temp)) ^ self.RCon[i//4-1]
            w[i] = w[i-4] ^ temp
        return [self.num_2_16bytes(
                    sum([w[4 * i] << 96, w[4*i+1] << 64, 
                         w[4*i+2] << 32, w[4*i+3]])
                    ) for i in range(11)]

    def AddRoundKey(self, State, RoundKeys, index):
        # 异或轮密钥
        return self._16bytes_xor(State, RoundKeys[index])

    def _16bytes_xor(self, _16bytes_1, _16bytes_2):
        return [_16bytes_1[i] ^ _16bytes_2[i] for i in range(16)]

    def _16bytes2num(cls, _16bytes):
        # 16字节转数字
        return int.from_bytes(_16bytes, byteorder = 'big')

    def num_2_16bytes(cls, num):
        # 数字转16字节
        return num.to_bytes(16, byteorder = 'big')

    def aes_encrypt(self, plaintext_list, RoundKeys):
        State = plaintext_list
        State = self.AddRoundKey(State, RoundKeys, 0)
        for Round in range(1, 10):
            State = self.SubBytes(State)
            State = self.ShiftRows(State)
            State = self.MixColumns(State)
            State = self.AddRoundKey(State, RoundKeys, Round)
        State = self.SubBytes(State)
        State = self.ShiftRows(State)
        State = self.AddRoundKey(State, RoundKeys, 10)
        return State

    def aes_decrypt(self, ciphertext_list, RoundKeys):
        State = ciphertext_list
        State = self.AddRoundKey(State, RoundKeys, 10)
        for Round in range(1, 10):
            State = self.ShiftRows_Inv(State)
            State = self.SubBytes_Inv(State)
            State = self.AddRoundKey(State, RoundKeys, 10-Round)
            State = self.MixColumns_Inv(State)
        State = self.ShiftRows_Inv(State)
        State = self.SubBytes_Inv(State)
        State = self.AddRoundKey(State, RoundKeys, 0)
        return State

如果对我的想法不太明白、或者觉得有些问题的师傅欢迎与我讨论！