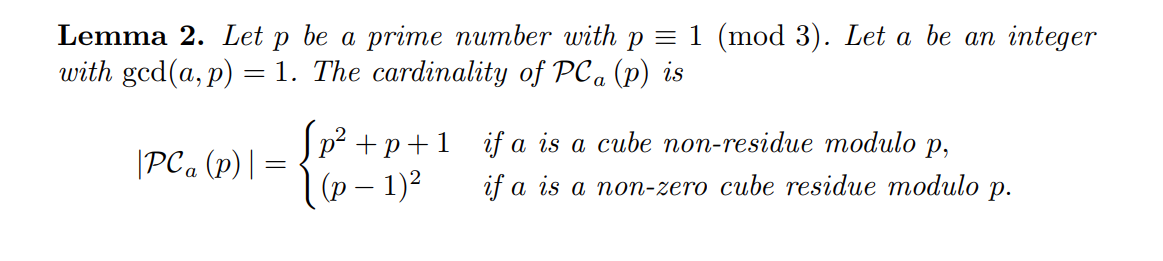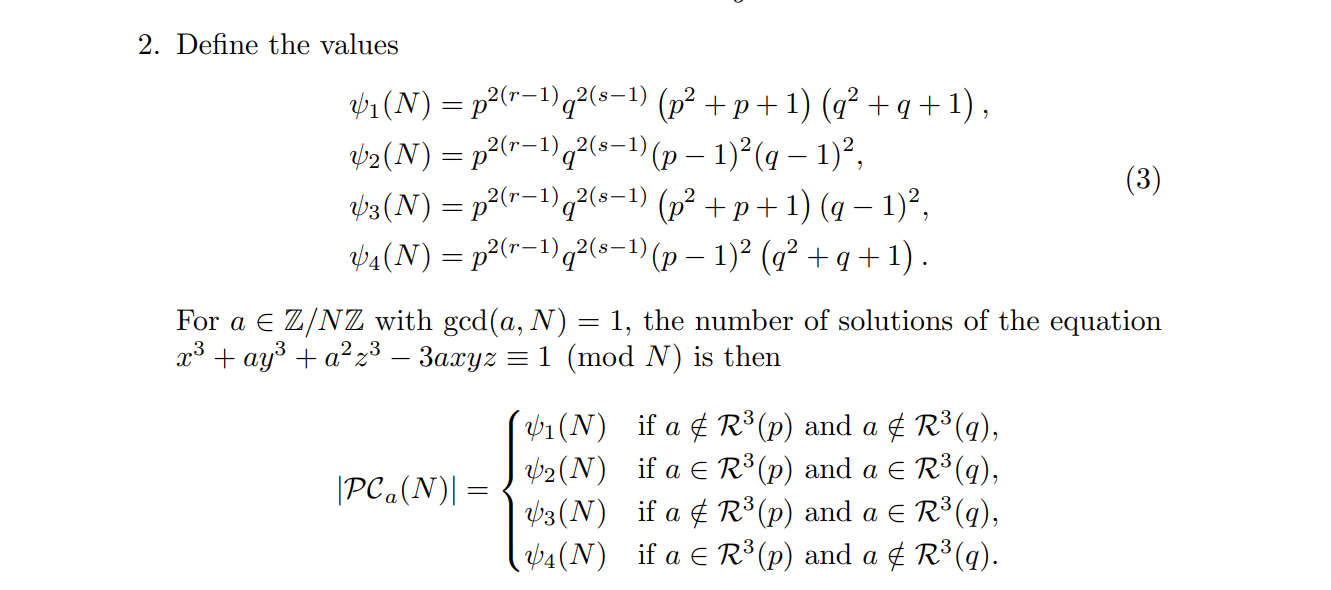不太清楚这个比赛是多久办的,不过赛后有师傅给我看了看三个基于Cubic Pell Curve的小题目,虽然难度都不高,但是这条曲线确实不算很常见,所以正好借此机会水一篇博客。
基础概念
Cubic Pell Curve方程形式如下:
这条曲线登场次数不多,不过近几个月倒是见过好几回了,分别是在DASCTFxHDCTF和CryptoCTF,总之关于他的加解密可以参考:
三个题目都是一些比较常见的问题搬到了这条曲线上做实现。
Pell Company’s A-level products
题目:
1 | from Crypto.Util.number import * |
题目随机生成64个曲线上的点$M_i$,并生成长64的01列表作为key,之后计算如下点当作密文:
仅给出$M_i$和$C$,要求解出列表key得到明文。
第一个地方在于题目没有给出曲线的参数a和p,但是由于我们有曲线方程形式以及多个曲线上的点,因此用几个点做groebner_basis就可以得到曲线参数了。
之后的问题在于如何恢复key,这个部分和我今年在NKCTF出的fly to the hyper一题很像,核心思路在于,我们拥有的式子其实很类似于一个01背包:
只是这里的背包元素不是数字而是点,没有办法直接做背包格规约,因此要想办法做点到数域的转换,转换的思路就是dlp。具体来说,如果我们找到曲线的生成元$G$,那么将所有点对$G$做DLP之后将会得到:
因此我们有:
此时就变成了我们熟悉的背包形式,不过这又引出了几个新问题:
- Cubic Pell Curve的阶是多少?
- 如何找到Cubic Pell Curve的生成元?
- 如何做DLP?
首先是求阶,直接factor一下p-1的话会发现非常的光滑,所以曲线的阶大概率是p-1的某个倍数了,用mul函数测一测就会发现正好是p-1。
要找理论依据的话可以看论文section3的Lemma2:
由于p的确是模3余1的,并且a也是三次剩余,所以曲线上阶应该是$(p-1)^2$,点阶是曲线阶的因子,所以阶是$p-1$很合理
接下来是找生成元,这里有个简单办法可以跳过这一步,注意到他的random_point是:
1 | def random_point(self): |
也就是说所有点都来自同一个$G$生成的点群内,那么当这次的k与点阶互素时,得到的新点也是$G$生成的循环群的生成元,所以从M中随便选一个当作$G$做就有一定概率成功。
最后是DLP,因为阶是光滑的,所以手写一个Pohlig-Hellman就行,这里偷了一点懒,其实可以在Pohlig-Hellman中间把点的重复倍乘换成逐次点加,并且用bsgs去加速,但是这个题求的并不算慢所以没啥必要优化。
之后就是做背包格规约,这里用优化的背包格+BKZ效果会好一些。
exp:
1 | from Crypto.Util.number import * |
Pell Company’s B-level products
题目:
1 | from Crypto.Util.number import * |
注意到题目中一个明显的点在于私钥d只有400bit,肯定算个小量,而曲线的阶也把四种可能性都给出了:
1 | if not cr_p and not cr_q: |
没给出的话可以参考论文的section3的Corollary4:
所以其实本质上是个低解密指数攻击,只需要逐个尝试阶是哪种情况去做copper就好, 会发现可以在第二种情况求解出题目的p、q和d来。
之后是要求明文,按加密方式来讲也就是要求出M,而为了求出M我们还需要求出a,才能对M的e倍点在曲线上做d倍的倍乘从而恢复M。而a的求解很简单,我们只需要代入$eM$的坐标$(x,y,z)$,然后分别在p、q下求解如下方程的根:
之后crt起来就行。
exp:
1 | from Crypto.Util.number import * |
Pell Company’s C-level products
题目:
1 | from sage.all import * |
这个题最容易,仅仅是把Cubic Pell Curve放到了模p下的二次扩域上来,我们唯一需要求解的就是曲线的阶从而求逆得到原点。
而由第二题中的曲线阶可以观察到,这种曲线的阶是分圆多项式或者$(p-1)^k$,而分圆多项式又是$p^k-1$的因子,所以我们只需要在小范围内把:
这样形式的阶都试一试就好了,就会发现$p^6-1$就是阶的一个倍数。
exp:
1 | from Crypto.Util.number import * |