糖醋小鸡块的blog
0%

2023-"科来杯"第十届山东省大学生网络安全技能大赛-wp-crypto

发表于 分类于 Valine：

没有参加这个比赛，但是赛后有师傅给我看了看题，发现其中那个pkrsa还挺有意思的，就简单写一写思路(没有赛题的交互环境也懒得自己搭，所以也就没有exp)

简单题也还是过一下吧。

小试牛刀

题目：

1
ipfm\x82Kj]p~l?\x82ogw\x85mt[K\x8br\x97

其实从前几个字符来看就能感觉到是变异凯撒。

exp：

1
2
3
4
5
6
7
diff = 3
c = b"ipfm\x82Kj]p~l?\x82ogw\x85mt[K\x8br\x97"
for i in c:
    print(chr(i-diff),end = "")
    diff += 1

#flag{CaSer_1s_VerY_E4sY}



easyrsa

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
# from Crypto.Util.number import getPrime,bytes_to_long
# from random import randint
# from gmpy2 import *
#
# m = bytes_to_long(b'flag{xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx}')
#
# p=getPrime(1024)
# q=getPrime(1024)
# n = p*q
# e = 65537
# c = pow(m,e,n)
# p_2=((p>>128)<<128)
# Result = []
# Divisor = []
# for i in range(12):
#     Divisor.append(getPrime(128))
# for i in range(12):
#     Result.append(p_2%Divisor[i])
#
#
#
# print(c,n,Divisor,Result)
'''
output:
16054555662735670936425135698617301522625617352711974775378018085049483927967003651984471094732778961987450487617897728621852600854484345808663403696158512839904349191158022682563472901550087364635161575687912122526167493016086640630984613666435283288866353681947903590213628040144325577647998437848946344633931992937352271399463078785332327186730871953277243410407484552901470691555490488556712819559438892801124838585002715833795502134862884856111394708824371654105577036165303992624642434847390330091288622115829512503199938437184013818346991753782044986977442761410847328002370819763626424000475687615269970113178 
23074300182218382842779838577755109134388231150042184365611196591882774842971145020868462509225850035185591216330538437377664511529214453059884932721754946462163672971091954096063580346591058058915705177143170741930264725419790244574761160599364476900422586525460981150535489695841064696962982002670256800489965431894477338710190086446895596651842542202922745215496409772520899845435760416159521297579623368414347408762466625792978844177386450506030983725234361868749543549687052221290158286459657697717436496769811720945731143244062649181615815707417418929020541958587698982776940334577355474770096580775243142909913
[205329935991133380974880368934928321273, 274334866497850560640212079966358515253, 264739757264805981824344553014559883169, 314495359937742744429284762852853819407, 197513216256198287285250395397676269263, 194633662721082002304170457215979299327, 320085578355926571635267449373645191637, 310701821184698431287158634968374845899, 198238777199475748910296932106553167589, 292201037703513010563101692415826269513, 332238634715339876614712914152080415649, 334257376383174624240445796871873866383]
[108968951841202413783269876008807200083, 29053101048844108651205043858001307413, 243503157837867321277650314313173163504, 160933173053376016589301282259056101279, 53063624128824890885455759542416407733, 34980025050049118752362228613379556692, 132553045879744579114934351230906284133, 160998336275894702559853722723725889989, 87211131829406574118795685545402094661, 36445723649693757315689763759472880579, 11133325919940126818459098315213891415, 1404668567372986395904813351317555162]
'''
from Crypto.Util.number import *
from gmpy2 import *
from functools import reduce

c=16054555662735670936425135698617301522625617352711974775378018085049483927967003651984471094732778961987450487617897728621852600854484345808663403696158512839904349191158022682563472901550087364635161575687912122526167493016086640630984613666435283288866353681947903590213628040144325577647998437848946344633931992937352271399463078785332327186730871953277243410407484552901470691555490488556712819559438892801124838585002715833795502134862884856111394708824371654105577036165303992624642434847390330091288622115829512503199938437184013818346991753782044986977442761410847328002370819763626424000475687615269970113178
n=23074300182218382842779838577755109134388231150042184365611196591882774842971145020868462509225850035185591216330538437377664511529214453059884932721754946462163672971091954096063580346591058058915705177143170741930264725419790244574761160599364476900422586525460981150535489695841064696962982002670256800489965431894477338710190086446895596651842542202922745215496409772520899845435760416159521297579623368414347408762466625792978844177386450506030983725234361868749543549687052221290158286459657697717436496769811720945731143244062649181615815707417418929020541958587698982776940334577355474770096580775243142909913
Divisor=[205329935991133380974880368934928321273, 274334866497850560640212079966358515253, 264739757264805981824344553014559883169, 314495359937742744429284762852853819407, 197513216256198287285250395397676269263, 194633662721082002304170457215979299327, 320085578355926571635267449373645191637, 310701821184698431287158634968374845899, 198238777199475748910296932106553167589, 292201037703513010563101692415826269513, 332238634715339876614712914152080415649, 334257376383174624240445796871873866383]
Result=[108968951841202413783269876008807200083, 29053101048844108651205043858001307413, 243503157837867321277650314313173163504, 160933173053376016589301282259056101279, 53063624128824890885455759542416407733, 34980025050049118752362228613379556692, 132553045879744579114934351230906284133, 160998336275894702559853722723725889989, 87211131829406574118795685545402094661, 36445723649693757315689763759472880579, 11133325919940126818459098315213891415, 1404668567372986395904813351317555162]

# def basic_CRT(ai,mi):
#     assert reduce(gmpy2.gcd,mi) == 1
#     assert len(ai) == len(mi)
#     N = reduce(lambda x,y:x * y,mi)
#     ans = 0
#     for a,m in zip(ai,mi):
#         t = N // m
#         ans += a * t * gmpy2.invert(t,m)
#     return ans % N,N
# result = basic_CRT(Result,Divisor)
# print(result)
#
# p_high=157397749849472741302651922559110947585741898399548366071672772026799823577871183957882637829089669634665699886533302712057712796808672023827078956556745522749244570015492585747076324258912525658578733402979835176037760966294532155059241756382643278063578661030876735794467422919824463419065126688059515994112
#
# PR.<x> = PolynomialRing(Zmod(n))
# f = x + p_high
# roots = f.small_roots(X=2^128, beta=0.4)
# if roots:
# 	p = p_high+int(roots[0])
# 	print("n="+str(n))
# 	print("p="+str(p))
# 	print("q="+str(n//p))
n=23074300182218382842779838577755109134388231150042184365611196591882774842971145020868462509225850035185591216330538437377664511529214453059884932721754946462163672971091954096063580346591058058915705177143170741930264725419790244574761160599364476900422586525460981150535489695841064696962982002670256800489965431894477338710190086446895596651842542202922745215496409772520899845435760416159521297579623368414347408762466625792978844177386450506030983725234361868749543549687052221290158286459657697717436496769811720945731143244062649181615815707417418929020541958587698982776940334577355474770096580775243142909913
p=157397749849472741302651922559110947585741898399548366071672772026799823577871183957882637829089669634665699886533302712057712796808672023827078956556745522749244570015492585747076324258912525658578733402979835176037760966294532155059241756382643278063578661030876735794708282102407491782299777228899079176117
q=146598666145389487374076474702380241089893944436923994466470555513748278755568038863819188404588602962888679358728628069490879689376996830110571995521814075973422513105805715524894550773219606972944401957227665252279176873209924236114228003156706532596699592716796867748104565680326123749660658940264843181589

e=65537
phi=(p-1)*(q-1)
d=invert(e,phi)
m=powmod(c,d,n)
print(long_to_bytes(m))
#b'flag{2233747d3bf06f070048e80300dac75f}'

额，我看到的题目就是这个样子的，exp和flag都写好了。不过实际看思路也很简单，就是先CRT求出p_2，然后高位攻击copper恢复p。



pkrsa

题目：

task.py：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from Crypto.Util.number import long_to_bytes,bytes_to_long,getPrime,GCD,inverse
from Crypto.Cipher import PKCS1_v1_5
from Crypto.PublicKey import RSA
import random

def generate_key(BITS):
	e = 3
	p = getPrime(BITS//2)
	q = getPrime(BITS//2)
	while GCD(e,(p-1)*(q-1)) != 1:
		p = getPrime(BITS//2)
		q = getPrime(BITS//2)
	n = p*q
	phi = (p-1)*(q-1)
	d = inverse(e,phi)
	return e,d,n
	
def sr(s):
	try:
		ans = raw_input(s)
		return ans
	except Exception as e:
		print(str(e))
		exit()

BITS=2048
print("generating......")
e,d,n = generate_key(BITS)
prikey=RSA.construct((n,e,d),)
key=PKCS1_v1_5.new(prikey)
print("n = "+str(n))
for _ in range(650):
	try:
		choice = sr("Your choice: ")
		if choice == '1':
			message = sr("Your msg: ")
			print(bytes_to_long(key.encrypt(message)))
		elif choice == '2':
			flag = open("flag").read()
			assert len(flag) == 38
			print(bytes_to_long(key.encrypt(flag)))
			exit()
	except Exception as ee:
		print(str(ee))
		exit()

除了task.py以外，题目还给出了一个Crypto库的具体实现，其列表如下：

image-20231025223218275

第一眼肯定会觉得这没什么用，但是其实另有玄机。不过这个后面再说，先分析一下题目加密流程：

解题关键

连接上靶机后，题目开始以如下方式生成RSA密钥：

1
2
3
4
5
6
BITS=2048
print("generating......")
e,d,n = generate_key(BITS)
prikey=RSA.construct((n,e,d),)
key=PKCS1_v1_5.new(prikey)
print("n = "+str(n))

其中，generate_key函数其实也没什么特别的地方，就是生成两个1024bit的大素数p、q且保证p-1、q-1与3互质，然后以加密指数e=3生成私钥并返回。然后以n、e、d生成了一个RSA加解密对象，然后下一行就是这道题目的真正重要之处：

1
key=PKCS1_v1_5.new(prikey)

而PKCS1_v1_5其实是对RSA加密解密的一种填充方式，这里其实也就是说他会将待加密的明文消息进行填充处理后，再利用RSA的公钥进行加密。

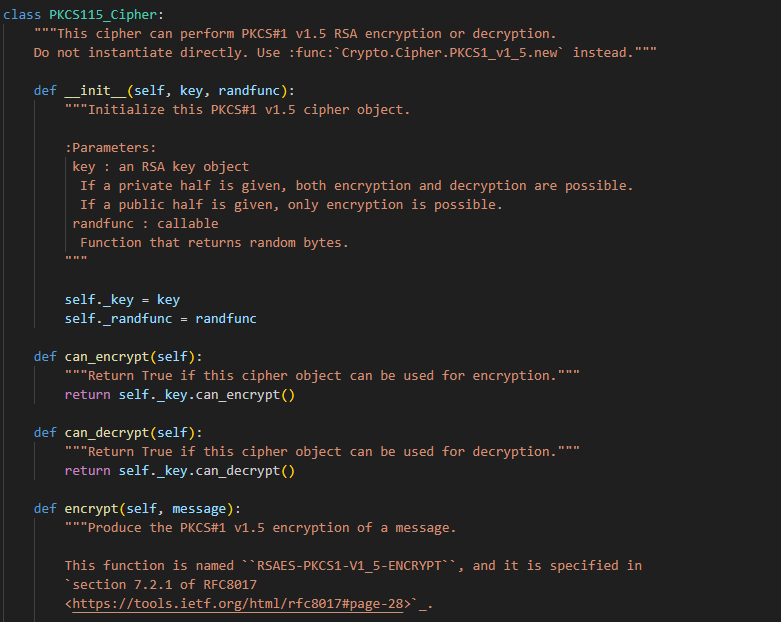
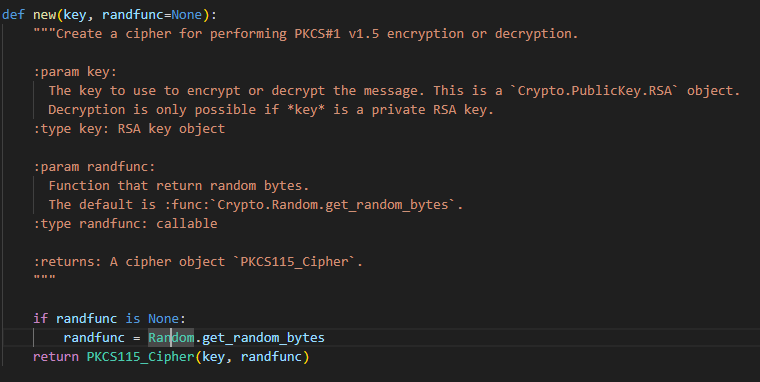
那么他的填充模式是什么呢？我们查看一下这个PKCS1_v1_5类的源码(从这里开始就已经踩坑了)：

image-20231025224232484

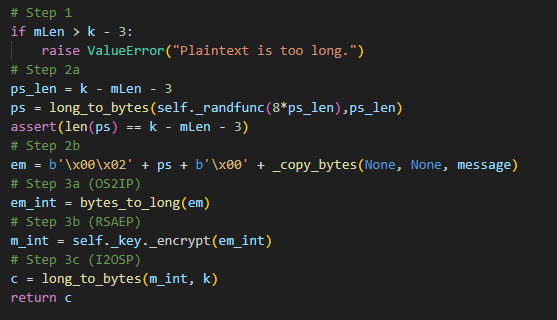
然后查看里面的encrypt函数，实现如下：

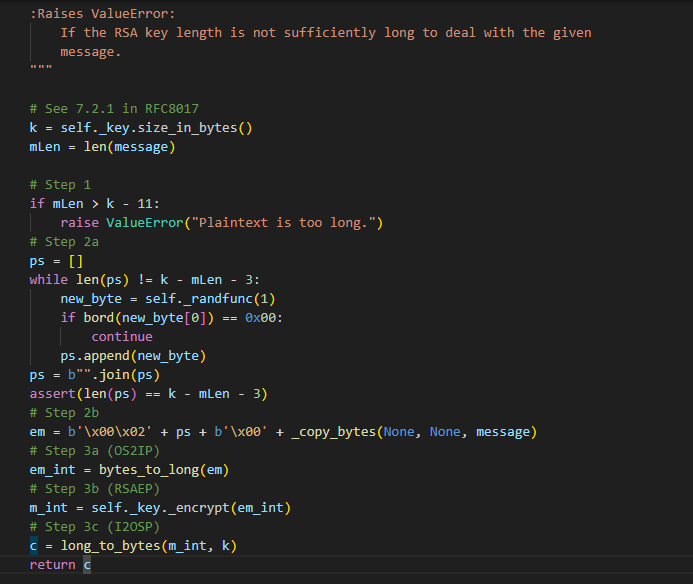
image-20231025224333992

最重要的是step 2a和step 2b的实现，具体来说，他是取了(k-mLen-3)长度的填充字节ps，ps是由self._randfunc函数一字节一字节生成的，并且保证不为0，然后待加密的消息就会被填充成如下格式：

1
em = b'\x00\x02' + ps + b'\x00' + _copy_bytes(None, None, message)

这样填充显而易见的好处是：

  • 可以防止低加密指数攻击
  • 可以正确解密，因为解密后截断b”\x00”前的填充字节就好

不过其实也是我自己随便想想的，建议还是自己了解一下这样填到底具体有些什么优缺点。

然后填充过后，就是正常的对em进行RSA加密得到密文了。而这个填充其实就是解决这个题目的核心所在，为什么是核心，之后会讲到。

题目任务

再回看这个题目交给我们的实际任务：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
for _ in range(650):
	try:
		choice = sr("Your choice: ")
		if choice == '1':
			message = sr("Your msg: ")
			print(bytes_to_long(key.encrypt(message)))
		elif choice == '2':
			flag = open("flag").read()
			assert len(flag) == 38
			print(bytes_to_long(key.encrypt(flag)))
			exit()
	except Exception as ee:
		print(str(ee))
		exit()

我们一共有650次机会可以进行如下交互：

  • 输入”1”，可以输入一个msg进行PKCS_v1_5的RSA填充加密，并返回密文
  • 输入”2”，可以得到对flag进行PKCS_v1_5的RSA填充加密得到的密文

那么其实思路就有了：通过前面交互得到的RSA的密文去解出每一次的填充，然后对最后一次的填充进行预测，从而copper解出明文。而这个伪随机数的预测其实很容易就能想到MT19937那一类的题型，我们检查一下他是不是用的getrandbits生成的随机填充：

那就一步步跟进函数源码，首先是encrypt函数内部的：

image-20231025225526921

跟进这个_randfunc，再跟进到类对象的初始化，可以看到：

image-20231025225611481

用的是Random库，跟进这个库看看：

image-20231025225646913

尴尬，怎么是用的urandom呢？因为这个生成的可以说是安全种子，而不像getrandbits那样，有足够的组数就可以进行后续随机数预测。

思路卡住了一会儿，突然想到：他不是给了一整个Crypto库的实现吗，也许意思就是在其中其实偷偷改动了一些函数与类的实现？而检查一下我们跟进的库，果然是本地的标准实现,而不是他给的：

image-20231025230001507

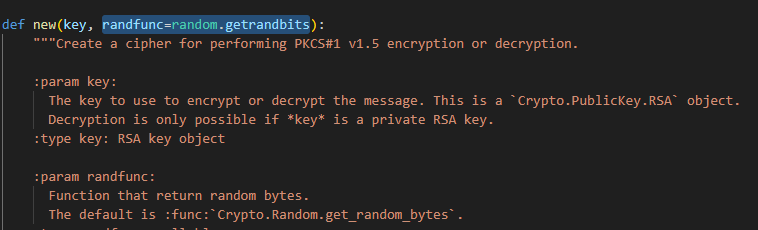
那就从头开始，用他给的库重新跟进，果然发现不一样的地方：

image-20231025230055075

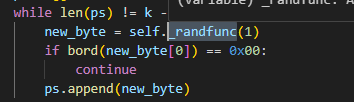
这个ps不再是逐字节生成的了，而是一次性生成完毕，而继续跟进，可以发现这里的_randfunc其实是：

image-20231025230158218

果然是getrandbits，多么的鸡贼！

那么思路就很清晰了，我们首先生成一个固定的245字节的明文，这样每次加密，靶机就会用getrandbits(64)生成8字节的填充块ps，也就是说，每一次我们有如下的关系式：

其中，num1是b”\x00\x02”对应的数字，ps是填充块对应的数字，msg是我们固定的消息。你应该已经可以想到了，每一次的ps都是一个64比特的小根，完全可以用copper解出来，那么312次后，我们就有312*64伪随机数比特，也就是足够的MT19937的state，就可以用randcrack库进行随机数预测了。这个时候我们就可以申请flag的加密结果了，有如下式子：

而这个时候ps_flag是我们能够预测的，flag又是一个38字节的小根，那就可以用copper求出flag了。

这题还是挺有意思，要自己去看源码内部的实现，而且结合了copper与MT19937伪随机数预测，所以记录一下。