糖醋小鸡块的blog
0%

2024-同济大学第二届网络安全新生赛CatCTF-wp-crypto

发表于 更新于 分类于 Valine：

负责了第二届新生赛Crypto的出题工作，全部wp在此。这里不会放输出文件（有点长），可以在官方仓库中找到：

CatCTF-2024/Crypto at main · Cat-Training-Force/CatCTF-2024 (github.com)

Week1

Week1主要是传统一点的密码题型。


Signin(75 Solves, 25/100 pts)

题目描述：

1
Bear heard sth like 'Caesar'?

题目：

1
6664776677697e583834714a62537536496c7b62666477667769623a33624934716762733777687551766272696246646876647580

题目描述里明确指出是凯撒，所以先解一下十六进制可以发现和已知的flag头”catctf”ASCII码差了3，所以再移位回去就好。生成密文脚本为：

1
2
3
from secret import flag

print("".join([hex((flag[i] + 3) % 256)[2:].zfill(2) for i in range(len(flag))]))

exp：

1
2
3
4
5
6
7
c = "6664776677697e583834714a62537536496c7b62666477667769623a33624934716762733777687551766272696246646876647580"
c = bytes.fromhex(c)

print("".join([chr((c[i] - 3) % 256) for i in range(len(c))]).encode())


#catctf{U51nG_Pr3Fix_catctf_70_F1nd_p4terNs_of_Caesar}



Double AES(10 Solves, 86/300 pts)

题目描述：

1
Bear accidentally got two ciphertexts of the same AES encryptor!

题目：

1
2
3
4
5
6
from Crypto.Util.Padding import pad
from Crypto.Cipher import AES
from secret import flag

key, iv = flag[:16].encode(), b"CatCTF2024"
print("c =", AES.new(key=key,nonce=iv,mode=AES.MODE_CTR).encrypt(pad(flag.encode(),16)) + AES.new(key=key,nonce=iv,mode=AES.MODE_CTR).encrypt(b"".join([pad(i.encode(),16) for i in flag])))

题目基于AES的CTR模式，用flag的前16个字节当作密钥，用”CatCTF2024”当作iv，然后分别加密：

  • 整体pad到十六字节整数倍的flag串
  • 逐字节pad到十六字节整数倍的flag串

题目将两个密文连接起来给出，要求还原flag。

首先我们要把两个密文分离开才行，为此我们需要确定flag长度，而确定flag长度的依据是密文长度。由于有pad的存在，密文以16字节为一组，其分组数量为：

这里其实并不准确，因为如果flag长度恰为16的整数倍的话pad会多一个分组

我们可以小范围遍历一下flag可能的字节数，判断其满不满足上面的式子，就可以确定下来flag的长度为49，从而分离两部分密文。

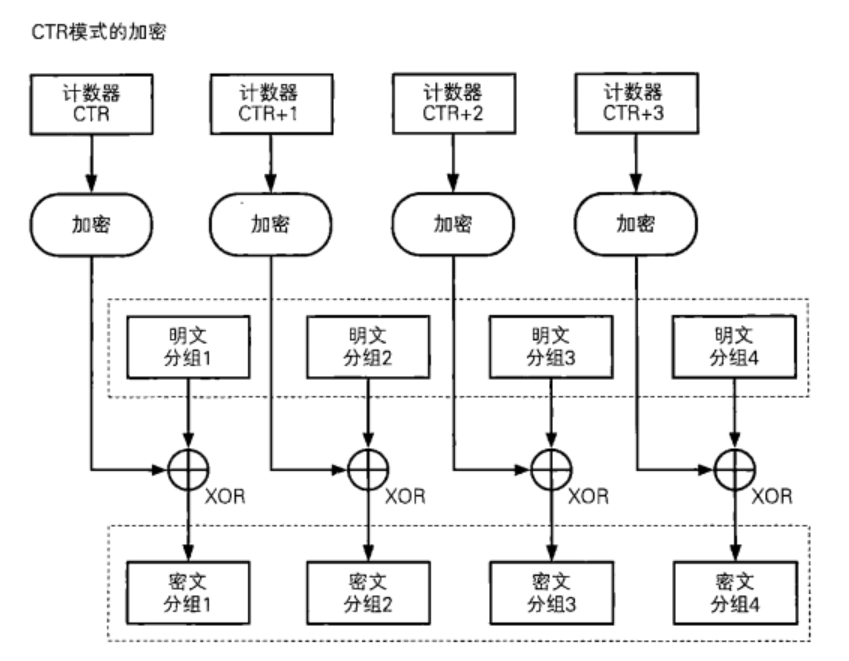
分离密文之后下一步就是恢复flag，为此需要了解一下CTR加密模式，以下是一个简单示意图：

image-20241006213955287

可以看出CTR模式加密步骤是：

  • 加密当前Counter
  • 将加密的Counter与当前分组明文异或，得到当前分组密文
  • Counter加一，用于下一分组加密

而由于加密两部分密文的密钥和起始Counter都一样，所以说他们异或的是同一个密钥流。而我们知道flag头，也就知道了第二部分密文第一个分组的明文是：

1
b"c" + b"\x0f"*15

将该明文与第一组密文异或就得到了第一组的密钥流，再与第一部分密文的第一组异或就得到了明文，而这个明文是key，就可以解得所有密文了。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Cipher import AES
from pwn import xor

c = b'\xbf\xa2\xe1P\x10\xcf4\x1a\x82\xd7M\xda\xd7?W\x8e!\xc2\xe0S\x93y\xbf\xaf\xe0l\xfdM\x0f\xb7\xac\xc0\x17\xd8\xa0+E\x97z\x95izN^\x84]yd\xdf\x8f\xcb\'\x17\x16m\xb0/5Z\xf6O\x97D\x03\xbf\xcc\x9a<k\xa6@@\xb8\xb1,\xb2\x87h\x17\xd3\x1f\x8d\x818\xc34\xc2\xd5\xd8P\xb4rr\xfb\xc6\x90!\xe6\x9fG\x01\xeb*\xd8\x1f*#\x1d\xc4\x11\x1dX\xc1\x8f\xcb\'\x17\x16m\xb0/5Z\xf6O\x97D\x03^\xa1E\t\x87\x90\xc9\xc5\x95{0K\x93g\xf8\r7\x9af\xa4X\x81\x0bF\x08\xf9\xe3\x01\xdf\'\xf7\x03I]\xb4T\x16H4(|\xb4 \xd3\x1f\x8b\xbe!\xefM\x11\x9cw\t$\t\x97\xc8\xf9\xe4\xcf\xe9\x91\xfa\x968s\xf8=\xbd\xf2k\xe6\x1f\xf6\xbeS\xcfH\xd6\x89_\xea\xc8\x7f8\xef?\xab\x07y\xdf\xc1\xf4\x1c\xb3\xe3\x18\x96\xbbR?\xe8\xfe\xc5[p\xe9\xa3\x91\xc3\xce\x86\xb2\xbc\xe4\t)J\x04\x86GC_y\xf7\x1b\xeb\xd7\x1c\x9al\x94\x93Tm\x99\xaf,J\x97q\x13\xaf\xb3\xd0\xc6]\x1d\n-\xfc\xae\xde"@\xff\xa6F\x96\xa5p\x1bZK\x82\x07\xe4XQh\xfa\x02\xcf\x06\x81\xbe\x12z\xe1V\xa1\xab\x7f+\xf9l\xea\x02\x1d\x91\xadq\xd9\x93\xb5\x1c\x8a\x8b\xf5\xcb\x8e\x0b\xbf\x17qw\xecR\xf7\xef\xe8\x11\x96\xc2\x85\xd0.\x9f&\x04\x7f\xeb:7\xbd\xaa\xb2|\x90\x16\x93\x81\xc1\x1b>h\x80n\xd3\xe4H7\xa8h\x9cp\xf8Z\xd9\xe1\xddfO\xac\x1eK\x90O\x12\xf4h=\xf1^\xc3\x01Vs\xea\xe6\xa1\xaeg\xb6\'f\xf6\xc8.J2\xc9\x96\x96\xd2\x9b\x17\xc8\x97\x05IX#\xff?\xae\xd9\x18\x86^zD;\xb1\xa1\xb1?\x11\x1d\xb9a\xe9\xff+\x16\xbc\x9b\xb2\xe5\x1d\xa0\xb8(]<aX\xb3\xc3\xfc\x1aU"\xfb\x1c\x80T\x11.\xc2\xa5A\xb4\xa8\xcetj\x91J\xdd\xc7B\xcc v\xbb\x8e\xc5DR#\x89\xb3m\xb2\xbc\xfa\xb0\xd7\xe8\x99\xf8\xa3\xc8\x00\xf2W\xafT\x92\x86\xfd\xf4=\x1a\x84)\xd3\x12\x16\xb0\xf7\x00\xfd\x18\xaf3\xe9\xc1,\xe1u\xb6\xc2z\xffbu1\x9f\xe1\x16\xb0b\x1f\xea\x00\n\xa6\xc7\r \xde\xcd\xf7~V\x19\'\x05\xc2\xcd>owY\xe9\xb2\xb4a\'\xb7\xf4+\x9d\x83\xd3\xd3`*]>\xea|\xb96\'\xd7in\x9a\x1d\xf1\x92\x86\x19\xb3Q#E\x99\xe9\xe0\x902~V\x94L\xe5\xb6\xbb\xdc\x16p\xce|\xd6%\xb7\xac\xb25\x92{%\xea\xa2\x0b\x0e\')zv\x18\xcc-A\x0e\x88\xb3\xfd\x07\xe4\x8d\xe1E~\x97DWe\xf9.\xd2Q\xb8a\xa2\'\xccS\xa6j\x8e\xcd\xb0\x80\x19\x8f\xa3\x98\xf0&Bq\x98\xe6dz\xc6V\x0e*\x8b6t\x8fF\xe6\xcc\x98P\xbe\xb5\xd0\x86\xd4\x17\xb3Iq\x08\x12<\xf6\xda\x7f\x8da\x8c\xe87\x02D\\@\x928\xcb\xc1O\x0fd\xe0\xfa\xa2\x8a;&\x14\x16g\x8f\xf6Ik\xae\x8fl,\xe0\xa1b\xfej\xdc\xc7$\x99\x95\xed\x0c$\x15\xa5n\xdeG\x02\x18&t"\xf8D\xb7T\xad=\x9cN`\x1e\xc3\xa3\x88\xde\x04[\\\x04)\x00\xcb\xb4+\x84T\xc5\x95\x04\t$\x1c\xa3sc\x17pppi\xd0\'\x1f3\x1d\xac\xf1\x98qU \x85\x01\x94\x80\x98\ri\x82\x1c\xf1nX\xa2&e\xd2B\x90\xc5\xee\x0bf_\xc6\xb9\xbaf\x1c\x11\x9c\x04\x07\xcc\x1d#'

if(0):
    for length in range(10,100):
        if((length//16)+1 + length == len(c)//16):
            print(length)

#length = 49 -> padding to 64
c1 = c[:64]
c2 = c[64:]
iv = b"CatCTF2024"
prefix = b"c"+b"\x0f"*15
key = xor(c1[:16], xor(prefix,c2[:16]))

flag = AES.new(key=key,nonce=iv,mode=AES.MODE_CTR).decrypt(c1)
print(flag)


#catctf{U5ing_XOR_@nd_Bru73F0rCe_B10cKs_By_bLOCk3}



Decision0(11 Solves, 83/300 pts)

题目描述：

1
why I call this Decision0? Maybe you will know next week.

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from Crypto.Util.number import *
from random import *
from secret import flag

flag_bin = bin(bytes_to_long(flag))[2:].zfill(len(flag)*8)

def F0():
    while(1):
        E = random_matrix(Zmod(n), 4, 4)
        if(E.rank() == 4):
            break
    return (E * Matrix(Zmod(n), 4, 4, [randint(0,3) for i in range(16)]) * E^(-1)).list()

def F1():
    while(1):
        T = random_matrix(Zmod(n), 4, 4)
        if(T.rank() == 4):
            return T.list()

n = 65537
print("output =", [F0() if i == "0" else F1() for i in flag_bin])

题目是一个按flag比特的decision：

  • 若当前bit为0，则输出：

    其中E为模65537下的随机满秩矩阵，A为由0-3的小值组成的矩阵。

  • 若当前bit为1，则输出：

    T为模65537下的随机满秩矩阵。

det

解题思路也很简单，若当前bit为1，那么C1的行列式也可以看作是模65537下的随机值。而如果当前bit为0，则有：

由于A由一些小值组成，所以其行列式在整数意义下较小，因此应该与65537的差值很小。通过此依据就可以对flag的每一bit做出decision。

trace

实际上，更进一步可以看出第一步的C和A是相似矩阵，所以其迹应该相等，因此计算C的迹，应该落在0-12以内，就可以做出decision。

优化

对于Decision类题目，有两个统一的优化在于：

  • 不用计算flag前后缀”catctf{}”对应的所有bit
  • 不用计算每个字节的MSB，因为可见字符MSB一定是0

这类优化对本题目效果不明显，但在单次bit判断耗时相对长时（如Decision3），能有效节省时间。

完整exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from Crypto.Util.number import *
from tqdm import *

output = 
output = output[7*8:-8]
n = 65537


#################################################### det
flag = ""
for bit in trange(len(output)):
    if(bit % 8 == 0):
        flag += "0"
        continue

    M = Matrix(Zmod(n), 4, 4, output[bit])
    if(min(n-M.det(), M.det()) < 200):
        flag += "0"
    else:
        flag += "1"
    
    if(bit % 8 == 7):
        print(long_to_bytes(int(flag,2)))


#################################################### trace
flag = ""
for bit in trange(len(output)):
    if(bit % 8 == 0):
        flag += "0"
        continue

    M = Matrix(Zmod(n), 4, 4, output[bit])
    if(int(M.trace()) <= 12):
        flag += "0"
    else:
        flag += "1"
    
    if(bit % 8 == 7):
        print(long_to_bytes(int(flag,2)))


#catctf{P@y_4tt3nT1on_70_Det}



C0pper(4 Solves, 157/300 pts)

题目描述：

1
What's the meaning of copper?

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import *
from os import urandom
from secret import flag

def pad(msg, length):
    return msg + urandom(length - len(msg))

m1 = bytes_to_long(pad(flag[:len(flag)//2],128))
m2 = bytes_to_long(pad(flag[len(flag)//2:],128))
p,q = getPrime(512),getPrime(512)
n = p*q

print("n =",n)
print("c1 =",pow(m1,3,n))
print("c2 =",(pow(m1,7,n) + getPrime(128)))
print("c3 =", pow(m2,333,n))
print("c4 =", pow(m2,667,n) + getPrime(128))
print("c5 =", pow(m2,997,n) + getPrime(128))

题目把flag分成前后两段，并随机padding后转为整数值m1、m2，之后生成RSA的私钥p、q及其乘积公钥n，然后给出五个密文(以下运算均在模n下进行)：

并给出n，要求还原m1、m2。其中e1、e2、e3都是128bit的素数，e是error的意思，也就是误差。

无误差情况下的求解思路

给我们制造麻烦的主要在于未知的e1、e2、e3，我们可以先想一想如果没有这几个误差我们能怎样恢复flag。比如对于c1、c2来说，我们就有两个在模n下以m1为根的多项式：

虽然n的分解未知的话，模下方程是难解的，但是既然有两个以m1为公共根的多项式，我们就可以求两个多项式的gcd，就会有一个公因式为：

就可以还原出m1，m2也同理可以还原。

有误差情况下的求解思路——coppersmith方法

而e1、e2、e3这些误差使得我们无法建立出这样的多项式组，但是我们可以注意到三个误差都仅有128bit，在模n下是比较小的，而正如题目名字一样，coppersmith提出了一种方法，这种方法可以求解分解未知的n下，多项式的小根。因此我们现在的任务变成了构建出以这些error为小根的多项式。

coppersmith方法的详细原理涉及格密码学，需要一定基础，有兴趣的可以自行搜索资料了解

入门的时候把这种方法当作黑盒调用即可，一般步骤为：

求解m1

那么对于m1，我们有：

所以我们有：

由此，按上面的步骤，我们可以建立出一个以e1为小根的多项式：

调用small_roots方法，就可以求出e1了。

得到e1之后，两个式子未知量就只剩下了m1，我们就又得到了两个以m1为公共根的多项式，因此求解多项式gcd即可得到m1。

求解m2

对于m2我们有三个式子：

按照求解m1的思路，似乎可以如法炮制出以e2为根的多项式：

但是实际操作下会发现求解不出来e2了，这是什么原因呢？

看一下m1和m2两部分，最显著的区别在于两部分的指数差异很大，m1指数较小，其对应多项式的度就小，仅为3；而m2指数较大，如果照同样的方法构造多项式的话，其指数为333，就大很多了。

而coppersmith方法求解小根的能力与多项式的度有强相关性，指数越小越利于coppersmith的求解，而333这种数量级已经远远超过了其求解能力，因此用同样的构造求解不了了。

多项式的度对于coppersmith小根上界为什么会有影响、究竟有什么影响，有兴趣的也可以自行翻阅资料

所以我们需要想别的构造，而突破点在于m2与m1的另一个区别——m2给了三组数据，所以我们要把三组结合起来一起用。而观察一下又可以发现，三组数据的指数是有很直接的关系的：

因此我们不妨做一个简单的换元处理：

那么就有：

而我们知道两个式子结合起来可以消掉一个未知量，而当前三个式子有：

共计四个未知量，那么用三个式子两两消元，就可以消去a、m2这两个未知量，从而得到一个含e2、e3且度较低的多项式。

此处使用的方法为结式(resultant)消元法，有兴趣的可以自行查阅相关资料

而这样的多项式就可以调刚才提过的多元coppersmith来求解e1、e2了，求出e1、e2之后仍然使用多项式gcd就可以得到m2。

完整exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
from Crypto.Util.number import *
import itertools

def small_roots(f, bounds, m=1, d=None):
	if not d:
		d = f.degree()

	R = f.base_ring()
	N = R.cardinality()
	
	f /= f.coefficients().pop(0)
	f = f.change_ring(ZZ)

	G = Sequence([], f.parent())
	for i in range(m+1):
		base = N^(m-i) * f^i
		for shifts in itertools.product(range(d), repeat=f.nvariables()):
			g = base * prod(map(power, f.variables(), shifts))
			G.append(g)

	B, monomials = G.coefficients_monomials()
	monomials = vector(monomials)

	factors = [monomial(*bounds) for monomial in monomials]
	for i, factor in enumerate(factors):
		B.rescale_col(i, factor)

	B = B.dense_matrix().LLL()

	B = B.change_ring(QQ)
	for i, factor in enumerate(factors):
		B.rescale_col(i, 1/factor)

	H = Sequence([], f.parent().change_ring(QQ))
	for h in filter(None, B*monomials):
		H.append(h)
		I = H.ideal()
		if I.dimension() == -1:
			H.pop()
		elif I.dimension() == 0:
			roots = []
			for root in I.variety(ring=ZZ):
				root = tuple(R(root[var]) for var in f.variables())
				roots.append(root)
			return roots

	return []


########################################################### data


########################################################### part1 univariate coppersmith
PR.<x> = PolynomialRing(Zmod(n))
f = (c2 - x)^3 - c1^7
f = f.monic()
res = f.small_roots(X=2^128,beta=1,epsilon=0.05)
a = int(res[0])


def gcd(g1, g2):
    while g2:
        g1, g2 = g2, g1 % g2
    return g1.monic()

PR.<x> = PolynomialRing(Zmod(n))
f1 = x^3 - c1
f2 = x^7 + a - c2
print(long_to_bytes(int(-gcd(f1,f2)[0])))


########################################################### part2 bivariate coppersmith
PR.<t,m,a,b> = PolynomialRing(Zmod(n))
f1 = t - c3
f2 = t^2*m + a - c4
f3 = t^3 + b*m^2 - c5*m^2

g1 = f1.sylvester_matrix(f2,t).det()
g2 = f1.sylvester_matrix(f3,t).det()
h = g1.sylvester_matrix(g2,m).det()
print(h)
PR.<a,b> = PolynomialRing(Zmod(n))
F = 
res = small_roots(F, (2^128,2^128), m=4,d=4)
a, b = int(res[0][0]), int(res[0][1])



def gcd(g1, g2):
    while g2:
        g1, g2 = g2, g1 % g2
    return g1.monic()

PR.<x> = PolynomialRing(Zmod(n))
f1 = x^333 - c3
f2 = x^667 + a - c4
print(long_to_bytes(int(-gcd(f1,f2)[0])))


#catctf{Un1vaRiate_c0pp3rSm1th_@nd_Biv4r1aTe_C0Pp3rSm1th_4ND_Fin@lLy_P0lyn0m1Als_GCD!}

还有一个比较简单的思路是找如下方程的小正整数解：

简单遍历一下小整数会得到一组解：

所以就有多项式：

多元copper即可。



Hash game(16 Solves, 76/300 pts)

题目描述：

1
Play a hash game with bear!

题目：

1
2
3
4
5
6
7
8
9
10
from random import *
from hashlib import *
from secret import flag

def SHUFFLE(t):
    temp = list(t)
    shuffle(temp)
    return "".join(temp)

print("c =", [SHUFFLE(choice([md5, sha1, sha384, sha256, sha512])(flag[:i]).hexdigest() + "".join([choice("0123456789abcdef") for _ in range(36)])) for i in range(1,len(flag)+1)])

题目基于哈希，总共给出flag长度那么多次密文，第i次的加密步骤为：

  • 从md5, sha1, sha384, sha256, sha512中随机选择一个当作本次的哈希函数，记为hashi

  • 将flag的前i个字符组成的串作为本次哈希对象，记为mi

  • 随机选择36个十六进制字符当作扰动，记为ei

  • 给出本次密文ci：

    其中加号为字符串连接，shuffle的作用是随机打乱字符串顺序

首先，对于每一个密文，我们要先判断出究竟其用的是哪一种哈希算法，而判断依据在于哈希值长度的不同。对于题目的五种算法来说，他们的哈希值长度分别为：

  • md5：128bit
  • sha1：160bit
  • sha256：256bit
  • sha384：384bit
  • sha512：512bit

而每个密文都会多出36个随机十六进制字符，因此十六进制长度减去36之后，就可以通过比特长度判断究竟是哪一种哈希算法了。

之后就是想办法还原flag，由于每一次哈希的对象是flag的前i个字符，因此第一次哈希对象就是flag的第一个字符，此时爆破空间很小，就是可见字符对应的ASCII码，也就是32-128内。

不过既然知道flag头”catctf{“，可以从第八个字符开始上述过程

此时我们可以用本次密文对应的哈希算法对这个小范围内所有字符逐个求哈希，但是由于每次密文做了如下处理：

  • 有36个随机十六进制字符扰动
  • 打乱了顺序

所以我们没办法直接通过对比哈希值是否相等，来判断当前究竟是哪个字符正确。然而，由于shuffle只会打乱顺序，不会改变哈希值每种十六进制字符的个数，因此对于正确的被哈希串来说，其一定会满足：

  • 哈希值的所有十六进制字符数量均小于等于对应密文十六进制字符数量

由此我们就可以找到一些符合条件的字符串，在这些字符串的基础上，我们继续向后搜索，用DFS的思路逐步减小范围，最后就可以得到正确的flag串了。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from hashlib import *

c = 

def check_chr(a, t1, t2):
    return t1.count(a) <= t2.count(a)   

noise_num = 36
def check_str(msg, t):
    if(len(t) == 32 + noise_num):
        return all(check_chr(a, md5(msg.encode()).hexdigest(), t) for a in "0123456789abcdef")
    elif(len(t) == 40 + noise_num):
        return all(check_chr(a, sha1(msg.encode()).hexdigest(), t) for a in "0123456789abcdef")
    elif(len(t) == 64 + noise_num):
        return all(check_chr(a, sha256(msg.encode()).hexdigest(), t) for a in "0123456789abcdef")
    elif(len(t) == 96 + noise_num):
        return all(check_chr(a, sha384(msg.encode()).hexdigest(), t) for a in "0123456789abcdef")
    elif(len(t) == 128 + noise_num):
        return all(check_chr(a, sha512(msg.encode()).hexdigest(), t) for a in "0123456789abcdef")

def find(flag):
    if(not check_str(flag, c[len(flag)-1])):
        return
    
    if(len(flag) == len(c)):
        print(flag)
        return
    
    for i in range(32,127):
        find(flag + chr(i))


find("c")


#catctf{Just_p1@Y_A_S1mP1E_H@SH_g4Me_W17H_DFS_I_gu3ss!}



Random game(3 Solves, 376/500 pts)

题目描述：

1
Play a random game with bear!

题目：

1
2
3
4
5
6
7
8
9
10
11
from Crypto.Util.number import *
from secret import flag
from random import *

gift = b"".join(long_to_bytes((pow(getrandbits(4), 2*i, 17) & 0xf) ^ getrandbits(8), 1) for i in range(4567))
m = list(flag)
for i in range(2024):
    shuffle(m)

print("gift =", bytes_to_long(gift))
print("c = '" +  "".join(list(map(chr,m))) + "'")

题目明显的分为了两个部分，一部分是getrandbits，一部分是shuffle。比较显然的解题步骤应该是：

  • 用gift实现伪随机数预测，从而确定shuffle如何进行
  • 逆向shuffle还原flag

本题wp也就分这两个部分展开。

getrandbits部分

MT19937的重要性质以及破解原理

python的random库中，几乎所有的函数都依赖于MT19937伪随机数生成，其具体原理及其他攻击方式可以参考：

MT19937 分析 | Xenny 的博客

浅析MT19937伪随机数生成算法-安全客 - 安全资讯平台 (anquanke.com)

我们这里不详细展开讲MT19937的详细算法内容，只需要了解该算法的几个性质，以及getrandbits实现的几个细节：

  • MT19937生成随机数前，会初始化一个state，state由624个32bit的数字组成，有了这个state，就可以往后任意预测随机数，不仅仅是getrandbits，random库里的几乎所有函数都可以预测其行为

  • 往后所有getrandbits产生的数字，都是关于这个初始state模2下线性的，这是破解MT19937的核心。用数学化一点的表述就是：

    • 把初始state二进制展开成一个长19968(624x32)的向量，记为$\textbf{s}$，该向量由0、1组成

    • 把getrandbits产生的任意位置的一个比特记为b

    • 那么一定存在一个向量$\textbf{t}$，使得：

      这就是线性关系的含义。

  • getrandbits是按照32bit为单位产生的，举几个例子就是：

    • 如果getrandbit(0)，会直接返回0，不会调用随机数生成
    • 如果getrandbit(32k)，那么会连续产生k个32bit的数并拼接起来
    • 如果getrandbits(t)，0<t<32，那么会先产生一个32bit的数字，然后截取其高t位作为本次随机数

以上就是做题需要了解的核心部分。

所以我们如果能拿到初始的state，就可以预测getrandbits的输出，乃至预测shuffle的行为。也就是说我们的目标是要求解那个长19968的01向量s，而求解依据就是刚才的线性关系式：

其中b是getrandbits产生的某个位置的比特，如果我们能搜集到19968个这样的等式，那么我们就可以把他们拼接起来，构建出一个矩阵方程：

如果T是满秩的，那么我们求解这个矩阵方程就可以得到s的唯一解，再把向量转回624个32bit的数字，也就得到了初始状态state。即使T不是满秩的，在模2下也可以简单遍历一下矩阵方程的解空间，其中就存在正确的s，所以依然可以获得state。

而为了解这个矩阵方程，我们需要有矩阵T和向量b，下面就开始针对题目讲解T和b的获取方式。

获取b

正如刚才所说，b是getrandbits的输出比特组成的向量，这些比特位置可以任意分布，但是我们需要知道他的位置来确定其线性关系。

而我们能获得的getrandbits的输出结果都在gift中，他是：

1
gift = b"".join(long_to_bytes((pow(getrandbits(4), 2*i, 17) & 0xf) ^ getrandbits(8), 1) for i in range(4567))

首先最直接可以获得的一些输出在于getrandbits(8)，我们可以发现每一轮给出的输出其实是getrandbits(8)异或一个4bit的数字，因此密文的高四位就是本次getrandbits(8)的高四位，如此一来我们就可以获得：

这么多个输出比特。

这并不够，正如上一节所讲的，我们需要19968个比特才行，还差一千多个。而我们可以发现与getrandbits(8)异或的部分是：

1
(pow(getrandbits(4), 2*i, 17) & 0xf) for i in range(4567)

17是个素数，由费马小定理我们可以知道：

实际上，由二次剩余的欧拉准则我们能进一步知道：

此时前者结果是1，后者结果是0。而如果a=0，那么结果是0。也就是说，当i为4的整数倍时，本次的：

1
(pow(getrandbits(4), 2*i, 17) & 0xf)

这个计算结果只能是0或1，这也代表着本次getrandbits(8)的高七位就是密文的高七位，所以我们总共能获得的比特数是：

这远远超过了19968，因此我们就获得了足够的输出比特，只需要选择其中19968个来解线性方程即可。把他们组合起来就得到了向量b：

事实上把已知的全取上为好，这样可以让约束更多，从而压缩s的解空间

获取T

我们回顾一下我们需要解的矩阵方程：

我们现在已经获取了b，只要能获取T，就可以解这个矩阵方程得到s了。

而T虽然我们暂时不知道，但是有一点可以确定：它是由MT19937本身算法得到的确定的线性关系，也就是说，我们如果拥有所有b的对应比特在MT19937产生的随机数流中的位置，那么其对应的T矩阵也是固定的。

我们的任务就是找到这个固定的T，而找的方式类似于黑盒调用。具体来说，如果我们取最开始的s为：

那么我们按照这个s设置初始state，然后调用getrandbits去生成我们已知位置对应的比特，得到b’，此时得到的b’其实就是T的第一行。同理，我们接下来继续令s为：

用这个s设置state，得到的b‘就是T的第二行。如法炮制我们就可以得到T的全部行。

有了T、b之后我们就可以解出初始state，有初始state之后我们可以将random的state设置为初始state，然后运行一遍gift，就来到了题目中shuffle前同样的状态。

shuffle部分

简单阅读一下random库的shuffle，源码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def shuffle(self, x, random=None):
    """Shuffle list x in place, and return None.

    Optional argument random is a 0-argument function returning a
    random float in [0.0, 1.0); if it is the default None, the
    standard random.random will be used.

    """

    if random is None:
        randbelow = self._randbelow
        for i in reversed(range(1, len(x))):
            # pick an element in x[:i+1] with which to exchange x[i]
            j = randbelow(i + 1)
            x[i], x[j] = x[j], x[i]
    else:
        _warn('The *random* parameter to shuffle() has been deprecated\n'
                'since Python 3.9 and will be removed in a subsequent '
                'version.',
                DeprecationWarning, 2)
        floor = _floor
        for i in reversed(range(1, len(x))):
            # pick an element in x[:i+1] with which to exchange x[i]
            j = floor(random() * (i + 1))
            x[i], x[j] = x[j], x[i]

可以看出，shuffle的实现原理是调用random库的randbelow函数来多次交换列表内的元素顺序，而我们现在拥有同样的初始状态，所以可以生成一个同样长度的列表，列表中的元素是索引。之后我们将这个列表shuffle2024次，就能看出flag对应的列表中的每个元素在经历2024次shuffle之后，究竟被交换到了什么样的位置，然后按对应索引将flag重新排序即可。

完整exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
from Crypto.Util.number import *
from random import *
from tqdm import *

gift = 
c = 'fUDs_|hUafdiE_eS)ecfna_rh|tu_ps(_1c}_efs___nfdHyilsseUfgt_Fho3is{3Lo_n_n1_u_uH||fFm_X'


######################################################### part1 recover MT and get seed
gift = long_to_bytes(gift)
RNG = Random()

def construct_a_row(RNG):
    row = []
    for i in range(len(gift)):
        RNG.getrandbits(4)
        if(i % 4 == 0):
            row += list(map(int, (bin(RNG.getrandbits(8) >> 1)[2:].zfill(7))))
        else:
            row += list(map(int, (bin(RNG.getrandbits(8) >> 4)[2:].zfill(4))))
    return row

L = []
for i in trange(19968):
    state = [0]*624
    temp = "0"*i + "1"*1 + "0"*(19968-1-i)
    for j in range(624):
        state[j] = int(temp[32*j:32*j+32],2)
    RNG.setstate((3,tuple(state+[624]),None))
    L.append(construct_a_row(RNG))

L = Matrix(GF(2),L)
R = []
for i in range(len(gift)):
    if(i % 4 == 0):
        R += list(map(int, (bin(gift[i] >> 1)[2:].zfill(7))))
    else:
        R += list(map(int, (bin(gift[i] >> 4)[2:].zfill(4))))

R = vector(GF(2),R)

s = L.solve_left(R)
init = "".join(list(map(str,s)))
state = []
for i in range(624):
    state.append(int(init[32*i:32*i+32],2))

RNG1 = Random()
RNG1.setstate((3,tuple(state+[624]),None))


######################################################### part2 set seed and recover shuffle
for i in range(4567):
    RNG1.getrandbits(4)
    RNG1.getrandbits(8)
x = [i for i in range(len(c))]

for i in range(2024):
    RNG1.shuffle(x)

flag = ""
for i in range(len(c)):
    flag += c[x.index(i)]
print(flag)


#catctf{_Shuf|fl3_s|hUFf1e_UnsHUff|L3_unsH|ufF1E_}



Week2

Week2为四道逐比特的Decision，方向稍微新一点，但是基本是考察这些新型方向的概念。


Decision1(4 solves, 241/400 pts)

题目描述：

1
Make your decision!

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from Crypto.Util.number import *
from random import *
from secret import flag

flag_bin = bin(bytes_to_long(flag))[2:].zfill(len(flag)*8)

def F0():
    f = lambda x: sum((poly[i])*pow(x,i,n) for i in range(len(poly))) % n
    poly = [randint(0,n) for _ in range(20)]
    return [f(j) + getrandbits(1) for j in range(40)]

def F1():
    return [randint(1,n) for j in range(40)]

n = 65537
print("output =", [F0() if i == "0" else F1() for i in flag_bin])

本题背景为格密码，其decision为：

  • 如果flag当前bit是1，则生成一个长度为40的模n下随机数组成的列表

  • 如果flag当前bit是0，则：

    • 生成一个长度为20的模n下随机数列表poly，poly代表着一个模n下的多项式f：

    • 用多项式f，生成一个长度为40的列表，列表中的元素为：

    其中ei取值为getrandbits(1)，也就是0或1。

我们需要判断出output中的每个列表究竟是用哪种方式生成的，从而决定当前bit是0还是1。

无误差情况下的求解——拉格朗日插值

由于当前bit为1的样本是随机值组成的列表，因此我们的思路显然是通过某种方法，来判断当前bit的样本是不是F0产生的样本。而注意到F0产生的列表中的每个元素，其实是多项式f上带误差的点值，也就是带误差的因变量y，而我们同时又知道每个y对应的自变量x就是0-39，所以其实我们拥有的是带误差的多项式点对，如下：

而有多组多项式点对，恢复多项式的其中一个办法就是拉格朗日插值法。具体来说，如果没有误差，那么我们可以建立如下矩阵方程：

我们的未知数只有poly对应的向量，并且左边的方程数有40个，变量仅有20个。那么我们根据ci构建出这个矩阵方程，如果有解就说明存在这样的poly，当前bit就一定是0了。而由于方程是超定的，所以对于当前bit为1产生的随机列表来说，其几乎不可能有解，因此就可以做出判断。

有误差情况下的求解——LWE样本判定

然而这样做的障碍在于本题的点值有1bit的随机误差ei，那么矩阵方程会变成：

此时由于误差e向量的存在，我们解不了矩阵方程了，就需要考虑其他办法。此时如果我们把矩阵方程抽象出来就是：

其中我们知道的信息有：

  • A、b的全部值
  • e是0、1组成的向量，在模n下是相当小的量

这其实就是一个典型的LWE样本，有关LWE的详细介绍我之前有写过：

LWE | 糖醋小鸡块的blog (tangcuxiaojikuai.xyz)

而判断一个样本是不是LWE样本，需要用到格密码的相关知识，而这一部分最常用到的有一个LLL函数。

LLL

和coppersmith一样，LLL的原理在这里不展开，入门时主要先掌握把它当作一个工具调用即可。他能做到的功能是：

  • 输入一组线性基向量

  • 输出这些基向量经线性组合后，得到的一些更短的基向量

    这里“更短”的含义可以理解为向量的长度更小，一定程度上也代表着向量中每个值都相对小

所以要用到LLL的题目的一般思路是：

  • 构造出题目对应的矩阵方程
  • 找到方程中由小的未知量构成的向量，这就是需要的短向量
  • 从矩阵方程中提取出经线性组合后，能够获得需要的短向量的基
  • 对这组基向量调用LLL，得到需要的短向量

我们接下来就照着这个步骤来完成一次解题。

利用LLL解决LWE样本判定

按照步骤，我们第一步需要构造出矩阵方程，这其实也就是带误差的拉格朗日插值方程：

接下来我们需要找到小的未知量构成的向量，很显然就是0、1组成的向量e。

第三步尤为关键，我们需要提取出一组经线性组合后能获得短向量的格基，这一步看上去并不容易。而实际上，线性组合的方式就蕴藏在第一步的矩阵方程中，我们不妨将矩阵方程进行转置：

可以发现，其实poly列表的左乘，就是对该矩阵行向量进行线性组合，而整个运算是模n下的，所以我们可以构造出如下的一矩阵，其行向量就是我们要找的一组线性基：

而对这个矩阵做如下的线性组合的话，就可以得到短向量：

由于e较小，所以这样得到的目标向量就较短，因此我们对将矩阵L作为LLL的输入进行调用，就可以在LLL的输出向量中找到我们需要的这个向量了。

事实上格基规约还需要进行一步操作叫配平（有时是为了规约出0而配大系数）。之所以要进行这个步骤，主要是因为LLL算法输出的基，会更倾向于向量中每个值数量级都相近的短向量

有更好的一种方式可以只规约出e，具体可以参考上面那篇LWE文章的primal attack2

而如果当前bit是1，其密文是随机值组成的列表，当然就很难有这么凑巧的线性组合，可以使得LLL之后输出这样的短向量，因此就可以通过LLL的输出结果对当前bit做出判断了。

完整exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
from Crypto.Util.number import *
from tqdm import *

#primal_attack2
def primal_attack2(A,b,m,n,p,esz):
    L = block_matrix(
        [
            [matrix(Zmod(p), A).T.echelon_form().change_ring(ZZ), 0],
            [matrix.zero(m - n, n).augment(matrix.identity(m - n) * p), 0],
            [matrix(ZZ, b), 1],
        ]
    )
    #print(L.dimensions())
    Q = diagonal_matrix([1]*m + [esz])
    L *= Q
    L = L.LLL()
    L /= Q
    res = L[0]
    if(all(i in [0,1,-1] for i in res) and abs(res[-1]) == 1):
        return True
    else:
        return False


output = 
output = output[7*8:-8]
n = 65537
nums = 40

flag = ""
for bit in trange(len(output)):
    if(bit % 8 == 0):
        flag += "0"
        continue

    A = Matrix(Zmod(n), 0, 20)
    b = []
    for i in range(nums):
        A = A.stack(vector(Zmod(n), [pow(i,j,n) for j in range(20)]))
        b.append(output[bit][i])
    A = Matrix(ZZ, A)
    b = vector(ZZ, b)
    check = primal_attack2(A,b,nums,20,n,1)

    if(check == True):
        flag += "0"
    else:
        flag += "1"
    
    if(bit % 8 == 7):
        print(long_to_bytes(int(flag,2)))


#catctf{l4gRanG3_@nD_LWE_s@mple!}

非预期解

事实上，由于多项式的度仅为19，因此在没有误差影响的情况下，利用拉格朗日插值方程，我们只需要20组数据就可以恢复多项式系数：

然而实际上题目是有误差的，但是我们可以爆破这20比特的误差，从而恢复多项式系数：

然后拿这多项式去计算后续值的函数值，检查误差是否仅有1比特即可。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
from Crypto.Util.number import *
from itertools import *
from tqdm import *


output = 
output = output[7*8:-8]
n = 65537
nums = 20

flag = ""
f = lambda x: sum((poly[i])*pow(x,i,n) for i in range(len(poly))) % n
for bit in trange(len(output)):
    if(bit % 8 == 0):
        flag += "0"
        continue
        
    A = Matrix(Zmod(n), 0, 20)
    b = []
    for i in range(nums):
        A = A.stack(vector(Zmod(n), [pow(i,j,n) for j in range(20)]))
        b.append(output[bit][i])
    A = Matrix(Zmod(n), A)
    b = vector(Zmod(n), b)
    invA = A^(-1)

    Found = 0
    for e in product([0,1],repeat=nums):
        e = vector(Zmod(n),e)
        poly = (invA*(b-e)).list()

        #check
        if(abs(int(f(20))-int(output[bit][20])) <= 1 and abs(int(f(21))-int(output[bit][21])) <= 1):
            Found = 1
            break

    if(Found == 1):
        flag += "0"
    else:
        flag += "1"
    
    if(bit % 8 == 7):
        print(long_to_bytes(int(flag,2)))


#catctf{l4gRanG3_@nD_LWE_s@mple!}

Decision1_revenge就是提高了维数的非预期修复版本，所以不单独写exp了。



Decision2(3 solves, 281/400 pts)

题目描述：

1
Make your decision again!

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from Crypto.Util.number import *
from random import *
from secret import flag

flag_bin = bin(bytes_to_long(flag))[2:].zfill(len(flag)*8)

p = 0x3cb868653d300b3fe80015554dd25db0fc01dcde95d4000000631bbd421715013955555555529c005c75d6c2ab00000000000ac79600d2abaaaaaaaaaaaaaa93eaf3ff000aaaaaaaaaaaaaaabeab000b
E = EllipticCurve(GF(p), (0, 4))
n = E.order()
primes = [67, 5563, 2099837, 773517157085353949]

def F0():
    r1 = choice(primes)
    r2 = choice(primes)
    return ((n // r1^2)*E.random_element()).weil_pairing((n // r1^2)*E.random_element(),r1) * ((n // r2^2)*E.random_element()).weil_pairing((n // r2^2)*E.random_element(),r2) % p

def F1():
    return GF(p).random_element()^((p-1) // prod(primes))

print("output =", [F0() if i == "0" else F1() for i in flag_bin])

本题背景为曲线配对，使用曲线为BLS12-638，其decision为：(以下运算均在模p下进行)

  • 如果flag当前bit是1，则返回的ci满足：

    其中a是模p下的随机数

  • 如果flag当前bit是0，则返回的ci满足：

    其中，P1、P2为题目给定曲线上的两个不同r1阶点，Q1、Q2为题目给定曲线上的两个不同r2阶点，r1、r2为从primes随机选择的两个值，e为weil pairing函数

为了解决这个题目，首先需要简单了解一下双线性配对函数的一些性质。

椭圆曲线上的双线性配对函数性质

简单来说，双线性配对可以理解成一个函数，其输入为椭圆曲线上的两个点，输出为椭圆曲线所在的域上的一个值。如果把这个函数记为e，那么这个概念可以写为：

其中F是椭圆曲线所在域。

双线性配对函数的一些重要性质如下：

  • $e(aP,bQ) = e(P,Q)^{ab}$

  • $e(P,P) = 1$

  • 对r-torsion中的点的配对，配对到的值均为曲线所在域的r次单位根

    此外还需要介绍一下torsion的概念，曲线上的r-torsion结构定义为所有满足$rP = O$的P点形成的集合，其中O点为曲线的单位元

而题目所用的weil pairing函数正是满足上述性质的一个双线性配对函数。

解题思路

flag当前bit为1的输出值能利用的点似乎并不多，因此我们还是主要关注flag当前bit为0的情况。由于P1、P2为曲线上的r1-torsion中的点，因此由上述性质可以知道，$e(P_1,P_2)$的结果是模p乘法群中的r1次单位根，也就是：

同理，对于r2-torsion中的Q1、Q2来说，就会有：

那么对于当前bit为0的输出来说，一定会有：

虽然我们并不知道r1、r2具体是primes中的哪两个值，但是我们可以遍历primes中所有两个因子的组合，那么对于当前bit为0的输出ci来说，一定存在一对r1、r2会满足上述等式。

r1、r2可能相同，但是如此遍历依然可以满足上述等式，因为两个r1次单位根的乘积依然是r1次单位根

而对于当前bit为1的输出，我们知道他是：

那么他经过上述遍历，得到的结果是：

r3、r4就是每次遍历中，primes剩下来的两个值，可以看出当且仅当a的阶为${\frac{p-1}{r_3r_4}}$的因子时上式才等于1，而这概率很小，因此就可以逐比特做出正确decision，进而还原flag。

完整exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from Crypto.Util.number import *
from itertools import *
from tqdm import *

output = 
output = output[7*8:-8]
p = 0x3cb868653d300b3fe80015554dd25db0fc01dcde95d4000000631bbd421715013955555555529c005c75d6c2ab00000000000ac79600d2abaaaaaaaaaaaaaa93eaf3ff000aaaaaaaaaaaaaaabeab000b
primes = [67, 5563, 2099837, 773517157085353949]

flag = ""
for bit in range(len(output)):
    if(bit % 8 == 0):
        flag += "0"
        continue

    Found = 0
    for i in combinations(primes, r=2):
        if(pow(output[bit], prod(i), p) == 1):
            Found = 1
            break

    if(Found == 1):
        flag += "0"
    else:
        flag += "1"
    
    if(bit % 8 == 7):
        print(long_to_bytes(int(flag,2)))


#catctf{M4p_70_Sp3c1al_Gr0uP}



Decision3(3 solves, 281/400 pts)

题目描述：

1
Make your decision aagain!

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from Crypto.Util.number import *
from random import *
from secret import flag

flag_bin = bin(bytes_to_long(flag))[2:].zfill(len(flag)*8)

p = 26734989077687468135677691953151
F.<i> = GF(p^2, modulus = x^2 + 1)
E = EllipticCurve(j=F(1728))

def iter():
    global E
    for i in range(10):
        P = E(0).division_points(randint(2,3))[1:]
        shuffle(P)
        phi = E.isogeny(P[0])
        E = phi.codomain()

def F0():
    iter()
    phi = E.isogeny(E(0).division_points(2)[1])
    E1 = phi.codomain()
    return (E.montgomery_model().a2() + getrandbits(13), E1.montgomery_model().a2() + randint(0,p))

def F1():
    iter()
    phi = E.isogeny(E(0).division_points(3)[1])
    E1 = phi.codomain()
    return (E.montgomery_model().a2() + getrandbits(13), E1.montgomery_model().a2() + randint(0,p))

print("output =", [F0() if i == "0" else F1() for i in flag_bin])

本题背景为曲线同源，先在一个给定的素数p下，生成一个二次扩域$GF(p^2)$下的超奇异椭圆曲线E，然后基于这个E开始进行后续步骤。

有关isogeny的知识我也写过一篇文章记录，有兴趣的同学可以看这篇帮助入门：

Isogeny | 糖醋小鸡块的blog (tangcuxiaojikuai.xyz)

当然，本题依然需要直接介绍其中一些概念，下方部分内容直接摘自上面这篇文章

本题的decision为：

  • 不论当前bit为1还是0，都会先基于刚才的曲线先进行十次2-isogeny或者3-isogeny，从而同源到一条新曲线上，这一步是为了通过起始曲线直接确定当前曲线

  • 如果flag当前bit是1，则进行一次3-isogeny，并且给出同源前后两条曲线Montgomery形式的a2，但是同源前的a2会有13bit误差，同源后的a2会有模p下的随机误差

  • 如果flag当前bit是0，则进行一次2-isogeny，并且给出同源前后两条曲线Montgomery形式的a2，但是同源前的a2会有13bit误差，同源后的a2会有模p下的随机误差

可以看出，我们主要是要判断出每一bit对应的同源究竟是2-isogeny还是3-isogeny，而其实不是2-isogeny就是3-isogeny，所以我们可以选择仅判断是否是2-isogeny，更为简单。

一些基本概念

超奇异椭圆曲线

若曲线E定义在有限域$F_{p^r} (r \in Z^*)$下，若E的阶order满足：

则E是一条超奇异椭圆曲线。

扩域

扩张的概念其实很简单。扩张也称作扩域，对于两个域来说，如果K是F的子域，F就是K的扩域或扩张。那么这里不妨选一个素数p，其为一个模4余3的大素数，则对于有限域$F_p$来说，他的二次扩张就是$F_{p^2}$。

而本题的同源就是在有限域$F_{p^2}$下工作的，这个有限域的大小是p^2，也就是说其中有p^2个元素。而这样一个有限域的元素有个最方便的表示方法，就是写成复数形式：

这样表示显然满足域的定义，因为首先它含有单位元1和零元0，并且满足：

  • $(F_{p^2},+)$是阿贝尔群
  • $(F_{p^2}-\{0\},\times)$是阿贝尔群
  • 乘法对加法满足分配律
曲线的Montgomery形式

对于蒙哥马利形的椭圆曲线来说，其曲线方程可以写成：

题目代码中的a2就是这个方程中的a，这是因为一条长Weierstrass形椭圆曲线的标准方程其实是：

而一般看到的是短Weierstrass形椭圆曲线，也就是：

这是因为在域特征不为2或3时，所有长Weierstrass形曲线都可以转化成短Weierstrass形曲线。

j不变量

对于椭圆曲线来说，j不变量可以简单理解为一个判定两条椭圆曲线是否同构的值。也就是说，任何一个曲线都有自己独特的j不变量，而如果两条曲线的j不变量相等，则说明这两条曲线彼此同构。而由于同构的曲线本质上都可以看作同一条曲线，这也就说明，一个j不变量其实在同构意义上其实就唯一对应着一条曲线。

曲线的Montgomery形式下，a与j不变量的关系

曲线在Montgomery形式下，a与他的j不变量满足如下方程：

modular polynomial

有一个比较有用的东西叫做modular polynomial，他的独特作用在于，能够用一个多项式关联d-isogeny中互为邻居的两个j不变量。也就是说，如果知道了一个j不变量，那么可以将其代入对应度的modular polynomial去求根，得到的所有根就是所有作为他的邻居的j不变量。其对应的度较低的多项式形式都可以在如下网站找到：

Modular polynomials (mit.edu)

解题思路

无误差情况下的求解

我们先假设我们得到的两条曲线的a2是无误差的。

我们从上面的预备知识知道，如果两条曲线是2-isogeny的邻居，那么他们的j不变量就会满足2-modular polynomial，也就是把两个j不变量代入下面的方程中，等式成立：

1
2
3
4
5
6
7
8
9
10
11
12
13
f = (
	X^3
	+ Y^3
	- X^2 * Y^2
	+ 1488 * X^2 * Y
	+ 1488 * X * Y^2
	- 162000 * X^2
	- 162000 * Y^2
	+ 40773375 * X * Y
	+ 8748000000 * X
	+ 8748000000 * Y
	- 157464000000000
)

而我们现在虽然不能直接得到两条曲线的j不变量，但是我们有两条曲线Montgomery形式下的a，因此可以通过下面的等式计算出j不变量来：

然后检查方程是否满足上面的2-modular polynomial，就可以判断当前bit是0还是1了。

有误差情况下的求解

然而，我们得到的曲线Montgomery形式下的a是有误差的，但是这误差有个特点就是：

  • 第一个误差仅有13bit，在可以枚举的范围
  • 两个误差都只涉及a的实部，虚部都是准确值

由于第一个误差很小，因此我们考虑在2^13范围内枚举第一个误差，那么我们可以看做我们拥有第一条曲线准确的a，也就可以计算出第一条曲线准确的j不变量。

而由于supersingular的同源曲线只能是supersingular的，所以对枚举到的超奇异曲线的j不变量，我们就可以代入到2-modular polynomial方程中，然后求根求出第二条曲线的j不变量，进而求出第二条曲线的a，然后我们只需要对比求出的这个a的虚部是否与给出a的虚部完全相同，就可以判断当前的两条曲线是不是2-isogeny的邻居，从而判断当前bit是0还是1。

完整exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
from Crypto.Util.number import *
from tqdm import *

p = 26734989077687468135677691953151
F.<i> = GF(p^2, modulus = x^2 + 1)

def check(j1,a2):
    PR.<Y> = PolynomialRing(F)
    X = j1
    f = (
            X^3
            + Y^3
            - X^2 * Y^2
            + 1488 * X^2 * Y
            + 1488 * X * Y^2
            - 162000 * X^2
            - 162000 * Y^2
            + 40773375 * X * Y
            + 8748000000 * X
            + 8748000000 * Y
            - 157464000000000
        )
    for i in f.roots():
        PR1.<a> = PolynomialRing(F)
        g = 256*(a^2-3)^3 - i[0]*(a^2-4)
        for j in g.roots():
            if((j[0] - a2)[1] == 0):
                return True
    return False


output = 
output = output[7*8:-8]
flag = ""
for bit in trange(len(output)):
    if(bit % 8 == 0):
        flag += "0"
        continue

    Found = 0
    for i in range(2^13):
        a = output[bit][0] - i
        J = F(256*(a^2-3)^3) / F(a^2-4)
        if(EllipticCurve(F,j=J).is_supersingular(proof=False)):
            res = check(J, output[bit][1])
            if(res == True):
                Found = 1
                break

    if(Found == 1):
        flag += "0"
    else:
        flag += "1"
    
    if(bit % 8 == 7):
        print(long_to_bytes(int(flag,2)))


#catctf{D1ffeRenT_M0duL@r_P0lynom1Al!}

多进程编程

赛中和做了本题的@TRiv1al交流了一下，我的exp大概需要四五十分钟，他的思路没有多大差别，然而他的exp却要跑十小时左右才行。排除一些实现上的细节问题的话，这个时间差异就只能是算力差异了。

而一个有效减少耗时的方式就是使用multiprocessing进行多进程编程，他的使用方法很简单，因此直接放exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
from Crypto.Util.number import *
from multiprocessing import Pool
from tqdm import *

p = 26734989077687468135677691953151
F.<i> = GF(p^2, modulus = x^2 + 1)

def check(j1,a2):
    PR.<Y> = PolynomialRing(F)
    X = j1
    f = (
            X^3
            + Y^3
            - X^2 * Y^2
            + 1488 * X^2 * Y
            + 1488 * X * Y^2
            - 162000 * X^2
            - 162000 * Y^2
            + 40773375 * X * Y
            + 8748000000 * X
            + 8748000000 * Y
            - 157464000000000
        )
    for i in f.roots():
        PR1.<a> = PolynomialRing(F)
        g = 256*(a^2-3)^3 - i[0]*(a^2-4)
        for j in g.roots():
            if((j[0] - a2)[1] == 0):
                return True
    return False

def attack(tup):
    bit, i = tup
    a = output[bit][0] - i
    J = F(256*(a^2-3)^3) / F(a^2-4)
    if(EllipticCurve(F,j=J).is_supersingular(proof=False)):
        res = check(J, output[bit][1])
        if(res == True):
            return True
    return False

output = 
output = output[7*8:-8]
flag = ""
for bit in trange(len(output)):
    if(bit % 8 == 0):
        flag += "0"
        continue

    Found = 0
    with Pool(8) as pool:
        r = list(pool.imap(attack, [(bit,i) for i in range(2^13)]))

    if(True in r):
        flag += "0"
    else:
        flag += "1"
    
    if(bit % 8 == 7):
        print(long_to_bytes(int(flag,2)))


#catctf{D1ffeRenT_M0duL@r_P0lynom1Al!}

这样子可以将时间缩短至十分钟左右。

注意这里Pool(8)并不代表着直接就可以将耗时缩短到单进程的1/8，因为这依然取决于你的CPU怎么样。但是一般来说使用多进程，对比起单进程肯定是有明显加速效果的。



Decision4(3 solves, 281/400 pts)

题目描述：

1
Make your decision aaagain! XD

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from Crypto.Util.number import *
from random import *
from secret import flag

flag_bin = bin(bytes_to_long(flag))[2:].zfill(len(flag)*8)
        
p = 65537
F = GF(p)
n, k = 40, 12
C = codes.GeneralizedReedSolomonCode(F.list()[:n], k)
Co = C.encoder()

def gen():
    temp = randint(0,n)
    return matrix(Permutation([i for i in range(1,n+1)][temp:] + [i for i in range(1,n+1)][:temp]))

def F0():
    err = [randint(1,p-1) for i in range(k)] + [0]*(n-k)
    shuffle(err)
    return (gen() * Co.encode(vector(F,[randint(0,p) for i in range(k)])) + gen() * vector(F,err)).list()
    
def F1():
    err = [randint(1,p-1) for i in range(k-1)] + [0]*(n-k+1)
    shuffle(err)
    return (gen() * Co.encode(vector(F,[randint(0,p) for i in range(k)])) + gen() * vector(F,err)).list()

print("output =", [F0() if i == "0" else F1() for i in flag_bin])

本题背景为编码理论，采用的编码是模65537下的(40,12)-Generalized Reed Solomon Code，其decision为：

  • 如果flag当前bit是1，则生成一个GRS的码字M，并生成一个weight为k-1的误差e，然后按如下方式计算得到密文向量ci：

    其中P1、P2是随机置换矩阵，共有40种可能性

  • 如果flag当前bit是0，其余部分与1完全一样，只是误差e的weight变成k，同样给出ci：

可以看出我们需要判断的内容，是误差e的weight究竟是多少。

GRS码的纠错能力为$\frac{n-k}{2}$，对于这个题目来说就是14，因此不论当前bit为0还是1，其误差e的weight都在纠错范围内，也就是可以进行纠错。而由于随机置换矩阵仅仅有40种可能性，因此我们小范围爆破，其中就存在正确的P1，那么我们可以左乘逆矩阵得到：

而由于e是一个可解码范围内的error，置换的复合$P_1^{-1}P_2$也仍然是个置换，不会改变e的weight，所以置换后的$P_1^{-1}P_2e$仍然是一个可解码范围内的error，所以我们对$P_1^{-1}\textbf{c}_i$做GRS码的decode，就可以得到正确码字M，自然也就可以得到e的weight从而进行decision。

需要注意不仅正确的$P_1^{-1}$能够解码，一些错误的${P’}_1^{-1}$依然能够成功解码，它们对应的是另外的正确码字和error，但当且仅当当前bit为1时才可能有error的weight为k-1。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from Crypto.Util.number import *
from tqdm import *

p = 65537
F = GF(p)
n, k = 40, 12
C = codes.GeneralizedReedSolomonCode(F.list()[:n], k)
Co = C.encoder()
D = C.decoder()

output = 
output = output[7*8:-8]

flag = ""
for bit in trange(len(output)):
    if(bit % 8 == 0):
        flag += "0"
        continue

    Found = 0
    for temp in range(n):
        P = Matrix(Zmod(p), matrix(Permutation([i for i in range(1,n+1)][temp:] + [i for i in range(1,n+1)][:temp])))
        codeword = P^(-1) * vector(F,output[bit])
        try:
            msg = D.decode_to_message(codeword).list()
            encodeword = Co.encode(vector(F,msg))
            err = codeword - encodeword
            if(err.list().count(0) == n-k+1):
                Found = 1
                break
        except:
            pass

    if(Found == 1):
        flag += "1"
    else:
        flag += "0"

    if(bit % 8 == 7):
        print(long_to_bytes(int(flag,2)))


#catctf{S1mplest_C0d1ng_SySt3M!}