糖醋小鸡块的blog
0%

Isogeny

发表于 更新于 分类于 Valine：

在今年N1CTF junior之后越发觉得还是很有必要学习一下同源，至少了解一些它的概念和性质。于是就跟着hashhash师傅给的一篇论文学了学，在这里用文字记录下来。

我会尽量用好懂一点的语言来阐述我的理解，因为本质上仅仅是入个门。如果有不准确的、错误的地方欢迎各位师傅指出。

参考文档指路

论文指路：

1321.pdf (iacr.org)

sage函数使用：

Isogenies - Elliptic curves (sagemath.org)



基本概念

具体来说，这篇学习笔记主要是围绕超奇异椭圆曲线同源的Diffie-Hellman(SIDH)，以及基于其的超奇异椭圆曲线同源密钥交换(SIKE)展开的，这些名词看着就相当复杂，所以先弄明白一些基础概念很有必要。


扩张(extension)

扩张的概念其实很简单。扩张也称作扩域，对于两个域来说，如果K是F的子域，F就是K的扩域或扩张。那么这里不妨选一个素数p，其为一个模4余3的大素数，则对于有限域$F_p$来说，他的二次扩张就是$F_{p^2}$。

而SIDH就是在有限域$F_{p^2}$下工作的，这个有限域的大小是p^2，也就是说其中有p^2个元素。而这样一个有限域的元素有个最方便的表示方法，就是写成复数形式：

这样表示显然满足域的定义，因为首先它含有单位元1和零元0，并且满足：

  • $(F_{p^2},+)$是阿贝尔群
  • $(F_{p^2}-\{0\},\times)$是阿贝尔群
  • 乘法对加法满足分配律

论文中取p=431，因此之后的所有情境就都放在$F_{431^2}$这个有限域下。


超奇异椭圆曲线(supersigular elliptic curve)

之前一直把超椭圆曲线(hyperellitic curve)和超奇异椭圆曲线当成差不多的东西，现在看来是个相当大的误解。超椭圆曲线以后有机会再展开说说，这里就只介绍一下超奇异椭圆曲线。

若曲线E定义在有限域$F_{p^r} (r \in Z^*)$下，若E的阶order满足：

则E是一条超奇异椭圆曲线。

用sage简单测试一下：

1
2
3
4
5
6
7
8
9
10
11
#example
p = 2^4*3^3-1
F.<i> = GF(p^2, modulus = x^2 + 1)

a1 = 208*i + 161
Ea1 = EllipticCurve(F,[0,a1,0,1,0])
print(Ea1.order() % p , Ea1.is_supersingular())

a2 = 208*i + 162
Ea2 = EllipticCurve(F,[0,a2,0,1,0])
print(Ea2.order() % p , Ea2.is_supersingular())
1
2
1 True
173 False


j不变量(j-invariant)

概念

对于椭圆曲线来说，j不变量可以简单理解为一个判定两条椭圆曲线是否同构的值。也就是说，任何一个曲线都有自己独特的j不变量，而如果两条曲线的j不变量相等，则说明这两条曲线彼此同构。而由于同构的曲线本质上都可以看作同一条曲线，这也就说明，一个j不变量其实在同构意义上其实就唯一对应着一条曲线。

而对于蒙哥马利形的椭圆曲线(Montgomery form)来说，其曲线方程可以写成：

他的j不变量的表达式就是：

我们简单验证一下论文里的$a_1 = 208i+161$和$a_2 = 172i+162$两种情况，计算他们各自的j不变量来判定两者是否同构，sage实现为：

1
2
3
4
5
6
7
8
9
10
11
12
13
#example
p = 2^4*3^3-1
F.<i> = GF(p^2, modulus = x^2 + 1)

a1 = 208*i + 161
Ea1 = EllipticCurve(F,[0,a1,0,1,0])
j1 = Ea1.j_invariant()

a2 = 172*i + 162
Ea2 = EllipticCurve(F,[0,a2,0,1,0])
j2 = Ea2.j_invariant()

print(j1 == j2)
1
True

因此这两条曲线是同构的，因为他们的j不变量相同。这也就是说，可以找到一个同构，将一条曲线映射到另一条曲线上。

相关性质

在这样的二次扩域下，所有p^2个元素也就可以看作是p^2个j不变量。而论文提及了一个事实，那就是其中包含着一个特殊的大小为$\lfloor \frac{p}{12} \rfloor + z,z \in \{0,1,2\}$的子集(其中z与p具体取值有关)，这个子集恰好包含了所有该二次扩域下超奇异椭圆曲线的j不变量。

比如对于论文中p=431的情境，二次扩域$F_{431^2}$下共有431^2个j不变量，而其中有一个大小为37的子集如下，使得该子集中所有元素都代表着同构意义下的一条超奇异椭圆曲线：

image-20240229102148144


同源(isogeny)

总体概念

同源本质上是一条曲线向另一条曲线上的映射(两条曲线也可以相同)。而之所以论文使用蒙哥马利曲线来做例子，是因为对于蒙哥马利曲线之间的映射来说，可以简单地只用x坐标之间的映射，就能表示出完整的映射。这是因为其映射形式为：

可以看出，只要确定了x坐标的映射函数f(x)，就可以唯一确定y坐标的映射而不会有多解。因为c是一个常数，不会有改变，而f’(x)是f(x)的导函数，由f(x)唯一确定。

因此映射可以简写为：

而映射的例子很容易举，就比如说，给定一条曲线E，将它上面的点都映射到他本身，这实际上就是个E到E的映射，只是没什么用而已。

进一步说，比如对于一条蒙哥马利曲线：

可以将E上的点都映射到他的二倍点，这也是一个E到E的映射，用仅含x坐标的简化形式就可以写为：

这里还要提一句，我们常见的椭圆曲线坐标，都是二维的仿射坐标，而这有一个小缺点就是没有办法表示无穷远点。而在三维的也就是椭圆曲线的射影坐标里就不存在这个问题，比如sage里，无穷远点通常就会用射影坐标表示成：

1
(0:1:0)

不过这里也不会展开说这些，提这一点的原因其实仅仅是因为，可以发现我们上面的映射好像没有办法表示出哪些点映射到了单位元(也就是无穷远点)，但是映射到单位元的点是很重要的，因为这些点构成的集合是这个映射的核(kernel)，而一个映射的核总是一个正规子群，就可以用来构造商群，也可以利用第一同构定理找出一个与映射的像(image)之间的同构。

说了这么一些，其实只是想说明一点——找出核是很重要的。而上面的映射形式其实已经能帮我们找出这个映射的核了，这是因为我们可以把分母为0的点看作无穷远点，那么映射的核里的点的横坐标就是分母代表的方程的解：

可以看出这个式子有三个解，分别是$0,\alpha,\frac{1}{\alpha}$，其中$\alpha$满足：

代入曲线方程就可以找到这个映射的核中的三个非平凡点：

又因为同态都具有一个性质，就是单位元也会映射到单位元，所以核中总共就含四个点：

可以看出，这个核是原曲线加法群上一个大小为4的子群(subgroup)。

而到现在就可以正式介绍同源的概念了，一个可分的(separable)同源可以描述为：对于一条曲线E以及E上一个子群G，都可以构造一个以G为核的映射$\phi: E \rightarrow E’$，这个映射就是同源，映射到的曲线$E’$就叫做这个同源的陪域(codomain)。

这里没有提到可分和不可分的概念区别(因为我也不知道)，大概可以理解成：如果一个同源可分，那么其映射后的f(x)的导数f’(x)不等于0；否则就是不可分的

如果用论文中更标准的Velu’s formulas的定义来说，同源可以描述成如下过程：

  • 输入一条曲线E，以及E上的一个子群G里的所有点
  • 输出陪域$E’=E/G$，以及对应的映射$\phi$
例子
1

首先举的例子就是刚才的二倍点的映射，这个同源的计算过程就是：

  • 输入E，以及子群$G=\{O,(0,0),(\alpha,0),(\frac{1}{\alpha},0)\}$
  • 输出E’(其实也就是E)，以及对应的映射$x \rightarrow \frac{(x^2-1)^2}{4x(x^2+ax+1)}$

这个可以用sage实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
#example
p = 2^4*3^3-1
F.<i> = GF(p^2, modulus = x^2 + 1)

a1 = 208*i + 161
E = EllipticCurve(F,[0,a1,0,1,0])
phi = E.scalar_multiplication(2)

E_ = phi.codomain()
fx = phi.rational_maps()[0] #only care about f(x)
print(E_ == E)
print(fx)
1
2
True
(x^4 - 2*x^2 + 1)/(4*x^3 + (-30*i + 213)*x^2 + 4*x)
2

可以发现，其实第一个例子举的子群G并不是一个循环群，因为群里除了单位元之外的元素阶都是2，因此没有生成元。而椭圆曲线虽然本身并不一定是一个循环群，但在其上任取一个点，都可以生成一个循环子群。就比如说我们取E上的$(\alpha,0)$这个点，他生成的就是一个阶为2的循环子群$G=\{O,(\alpha,0)\}$，那么我们可以用这个子群和曲线E生成一个同源，表示为：

  • 输入E，以及子群$G=\{O,(\alpha,0)\}$
  • 输出E’，以及对应的映射

而此时的E’就不再是原来的曲线E了，他的j不变量发生了变化。然而有一点不会变：E’依然是条超奇异椭圆曲线。

我们用代码验证一下，首先可以用如下方式求出曲线上所有阶为2的点：

1
2
torsion_2_points = E(0).division_points(2)
print(torsion_2_points)
1
[(0 : 0 : 1), (0 : 1 : 0), (350*i + 68 : 0 : 1), (304*i + 202 : 0 : 1)]

然后就取$\alpha = 350i + 68$，由于他的所有倍点产生的是一个循环子群，所以整个子群G可以就用该点来表示，因此计算这个同源的代码可以写为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#example
p = 2^4*3^3-1
F.<i> = GF(p^2, modulus = x^2 + 1)

a1 = 208*i + 161
E = EllipticCurve(F,[0,a1,0,1,0])

alpha = E(0).division_points(2)[2]
phi = E.isogeny(alpha)

E_ = phi.codomain()
print(E_.montgomery_model())
print(E_.j_invariant())
print(phi.rational_maps()[0])
1
2
3
Elliptic Curve defined by y^2 = x^3 + (102*i+423)*x^2 + x over Finite Field in i of size 431^2
344*i + 190
(x^2 + (81*i - 68)*x + (190*i - 214))/(x + (81*i - 68))


扩展概念与性质

最基本的同源概念就说完了。总结一下其性质有：

  • 同一条曲线上，一个唯一的子群对应唯一的同源

  • 同源本质上是一种同态，因此它具有同态的性质，也就是：

  • 同源可以进行复合运算

  • 一个同源拥有一个唯一的对偶同源，他们度相等，并且这两个同源复合后等价于曲线向其度倍点上的同源

    这里对偶同源的概念其实和逆同态很类似，只是他们复合后并不是恒等映射，这是同源的特殊性质

这里又牵扯出了一些新概念，比如同源的度，以及刚才代码里出现的torsion一词，这里对这两个词简单解释一下。

同源的度其实就是同源的核的大小，也可以定义为同源映射后f(x)分子和分母的多项式的度的最大值。对于度为d的同源，可以记为d-isogeny。

比如刚才举的两个例子，对于第一个同源来说，其核为$G=\{O,(0,0),(\alpha,0),(\frac{1}{\alpha},0)\}$，大小为4，所以该同源度为4；也可以说其f(x)中分子分母度的最大值为4，所以同源度为4。对于第二个同源，同理可得其度为2。

而torsion的概念指的又是什么呢？我查了一些代数几何和拓扑几何的概念，发现中文的翻译为”扭”或者”挠”，感觉并不是很好听所以我在后面也就直称他为torsion。而torsion在群论，或者说其在椭圆曲线中的定义，就是所有满足：

的P点形成的集合，就叫做$l-torsion$。

比如说刚才提到的二倍点映射的核$G=\{O,(0,0),(\alpha,0),(\frac{1}{\alpha},0)\}$其实就是E上的一个2-torsion，其结构可以画为：

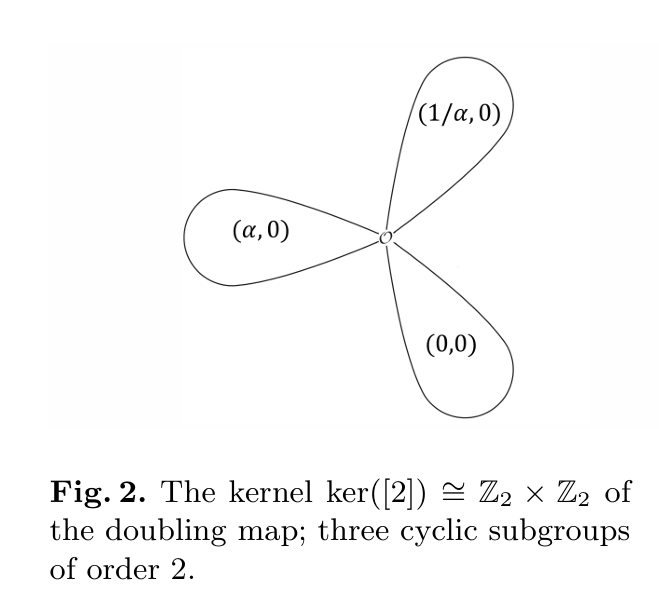
image-20240229115730410

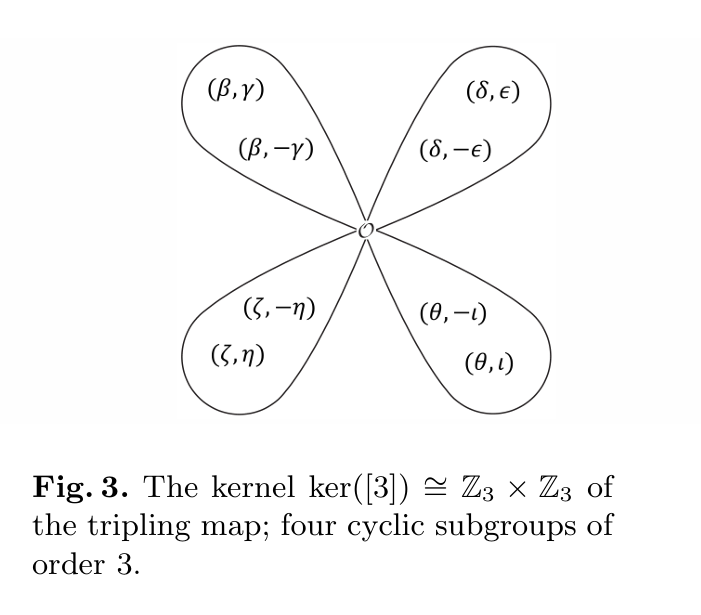
同理，3-torsion也可以画为：

image-20240229115759660


同源图(isogeny graph)

还是举刚才同源的第二个例子，可以看出我们取的点是2-torsion中的一个点，其生成的循环子群G大小也就是2，用这个子群G与曲线E就能生成一个同源，它将E映射到E’，这使得j不变量发生了变化：

而2-torsion中除去单位元还有两个点，分别取他们来生成循环子群，也可以和原曲线E生成同源，j不变量分别会发生如下变化：

而回顾刚才我们给出的$F_{431^2}$上的所有超奇异椭圆曲线的j不变量的图：

image-20240229120631360

可以发现，整个E的2-torsion其实给出了三条边，他们的起点是E的j不变量对应的点，终点是映射到的E’的j不变量对应的点。而如果对所有点的2-torsion都画出这些边，就得到了完整的2-isogeny的同源图，他能表示出这个二次扩域中所有度为2的isogeny的映射关系：

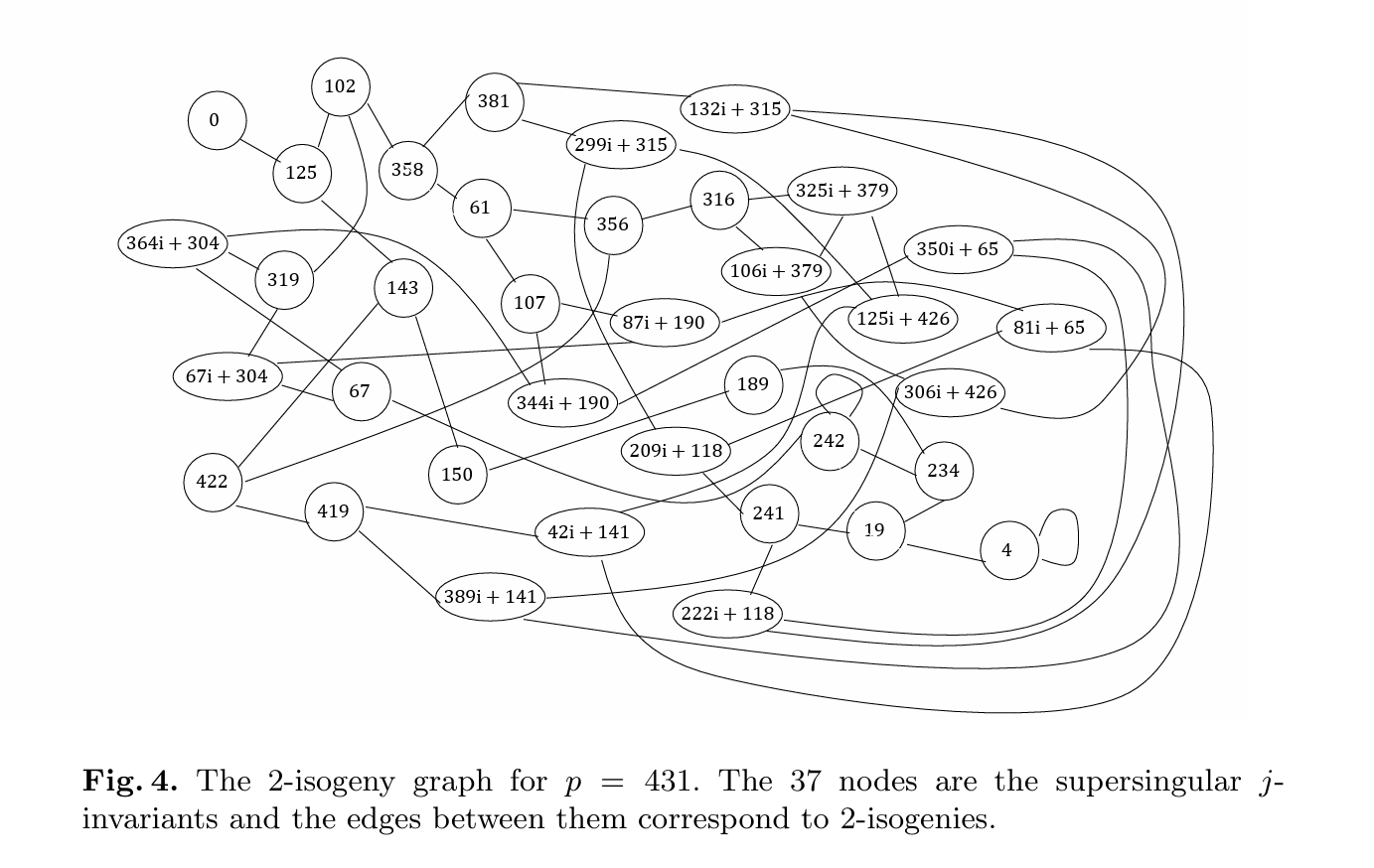
image-20240229120909653

而之所以边是无向的，就是因为我们刚才提过的对偶映射，如果E向E’有个度为2的同源，那么E’向E也一定有一个度为2的对偶同源。可以发现图中大多数点都是有三个邻居的，因为他们的2-torsion除去单位元都有三个点；但也有一些点比如0、4、242有些特殊，要么邻居数不够，要么邻居有自己(也就是产生了环)，这里就不详细展开这种情况了，知道有特殊的一些点就好。

因此，在同一个二次扩域下，度为2的所有超奇异椭圆曲线同源生成了一张同源图，他指示出了度为2的同源会如何在点之间移动。同理，度为3乃至更高的同源图也可以如此绘制出来，指示出对应度的同源的点之间的移动关系。

而绘制出同源图也更好理解同源之间的复合，比如对于如下移动路径：

他可以看作是两个度为2的同源的复合，也可以看作是单独的一个度为4的同源。这同时说明度为d^e的同源可以拆解为e个度为d的同源，从而变成d-isogeny图中一条长为e的路径。


modular polynomial

此外，还有一个比较有用的东西叫做modular polynomial，他的独特作用是用一个多项式关联了d-isogeny中互为邻居的两个j不变量。也就是说，如果知道了一个j不变量，那么可以将其代入对应度的modular polynomial去求根，得到的所有根就是所有作为他的邻居的j不变量。

这为一些中间相遇提供了快速计算的便利，modular polynomial对应的度较低的多项式形式都可以在如下网站找到：

Modular polynomials (mit.edu)



超奇异椭圆曲线同源密钥交换

流程

基本概念说得差不多了，下面就来讲一讲利用同源如何进行Diffie-Hellman的密钥交换。首先他选择如下形式的素数式：

并定义其二次扩域上的超奇异椭圆曲线E。在下文的情境中依然使用论文选择的参数：

满足：

此后，Alice与Bob想利用SIDH交换一个共享密钥。对于Alice来说，他选择曲线上阶为$2^{e_A}$的两个点$P_A,Q_A$。注意这里要求这两个点不在同一个循环子群中，也就是其中一个点不能被另一个点表示出来。这一点可以用weil配对是否为1来验证(线性配对这里也不展开了，有机会再说)。比如在论文情境中，他选择了如下两点：

可以验证一下这两个点是否满足刚才的性质：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#part1 construct supersingular ECC on F_p2
p = 2^4*3^3-1
F.<i> = GF(p^2, modulus = x**2 + 1)
a0 = 329*i+423

E = EllipticCurve(F,[0,a0,0,1,0])
assert E.j_invariant() == 87*i + 190
assert E.is_supersingular()


#part2 Alice's and Bob's public points
PA = E(100*i+248,304*i+199)
QA = E(426*i+394,51*i+79)
assert PA.order() == 2^4
assert QA.order() == 2^4
assert PA.weil_pairing(QA,2^4) != 1

可以发现是满足的。同理，Bob选择两个阶为$3^{e_B}$的两个点$P_B,Q_B$。这四个点都是公开的参数。

之后，Alice在$k_A \in [0,2^{e_A})$中选择他的秘密私钥kA，在论文给的具体情境里也就是在0到15中选择kA，并计算：

这里可以简单证明一些事情：

  • SA是一个阶为16的点
  • SA生成的阶为16的循环子群与PA、QA生成的不相同

先证明第一点，因为显然有$16S_A = 16(P_A + k_AQ_A) = O$，所以SA的阶只会是16的因子；又因为$8S_A = 8P_A + 8k_AQ_A$，若有$8S_A = O$，就有$8P_A + 8k_AQ_A = O$，则PA可以表示为QA的倍点，与假设矛盾。因此SA阶为16

证明了第一点，第二点就很轻松了，比如假设SA生成的循环子群和PA生成的相同，那么任意一个SA的倍点也就都可以用PA的倍点表示，则PA可以表示为QA的倍点，与假设矛盾。

通过上述说明可以发现，我们这样选择的SA形成了一个新的阶为16的循环子群(虽然选0的时候并不是)。而从前面对同源的介绍来说，一条曲线和其上一个唯一的子群就会构成一个唯一的同源。因此我们就可以计算E和SA产生的同源，记为$\phi_A$，并计算Bob公开的两个点PB、QB经$\phi_A$映射后的坐标$\phi_A(P_B),\phi_A(Q_B)$，如此就形成了Alice的全部公钥：

其私钥为$S_A,\phi_A,k_A$

同理，Bob同样经历上述过程，其全部公钥就是：

其私钥为$S_B,\phi_B,k_B$

我们代入具体的数字$K_A = 11,k_B = 2$，就可以把这个过程用代码展示出来：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
#part1 construct supersingular ECC on F_p2
p = 2^4*3^3-1
F.<i> = GF(p^2, modulus = x**2 + 1)
a0 = 329*i+423

E = EllipticCurve(F,[0,a0,0,1,0])
assert E.j_invariant() == 87*i + 190
assert E.is_supersingular()


#part2 Alice's and Bob's public points
PA = E(100*i+248,304*i+199)
QA = E(426*i+394,51*i+79)
assert PA.order() == 2^4
assert QA.order() == 2^4
PB = E(358*i+275,410*i+104)
QB = E(20*i+185,281*i+239)
assert PB.order() == 3^3
assert QB.order() == 3^3


#part3 Alice choose secret kA and gen Alice's public key
if(1):
    kA = 11
    SA = PA + kA*QA
    S_A = SA
    assert SA.order() == 2^4

    #compute phi0
    RA = 2^3*S_A
    phi0 = E.isogeny(RA)
    Ea1 = phi0.codomain()
    S_A = phi0(S_A)
    #print(Ea1.montgomery_model())
    #print(Ea1.j_invariant())
    #print(S_A)


    #compute phi1
    RA = 2^2*S_A
    phi1 = Ea1.isogeny(RA)
    Ea2 = phi1.codomain()
    S_A = phi1(S_A)
    #print(Ea2.montgomery_model())
    #print(Ea2.j_invariant())
    #print(S_A)


    #compute phi2
    RA = 2*S_A
    phi2 = Ea2.isogeny(RA)
    Ea3 = phi2.codomain()
    S_A = phi2(S_A)
    #print(Ea3.montgomery_model())
    #print(Ea3.j_invariant())
    #print(S_A)


    #compute phi3
    RA = S_A
    phi3 = Ea3.isogeny(RA)
    Ea4 = phi3.codomain()
    S_A = phi3(S_A)
    #print(Ea4.montgomery_model())
    #print(Ea4.j_invariant())
    #print(S_A)

    
    #compute phiA
    phiA = phi3*phi2*phi1*phi0
    #print(phiA.codomain().montgomery_model())
    print("pathA =(",E.j_invariant(),")->(",Ea1.j_invariant(),")->(",Ea2.j_invariant(),")->(",Ea3.j_invariant(),")->(",Ea4.j_invariant(),")")
    PKA = (phiA.codomain(),phiA(PB),phiA(QB))
    print(PKA)


#part4 Bob choose secret kB and gen Bob's public key
if(1):
    kB = 2
    SB = PB + kB*QB
    S_B = SB
    assert SB.order() == 3^3

    #compute phi0
    RB = 3^2*S_B
    phi0 = E.isogeny(RB)
    Ea1 = phi0.codomain()
    S_B = phi0(S_B)
    #print(Ea1.montgomery_model())
    #print(Ea1.j_invariant())
    #print(S_B)

    
    #compute phi1
    RB = 3*S_B
    phi1 = Ea1.isogeny(RB)
    Ea2 = phi1.codomain()
    S_B = phi1(S_B)
    #print(Ea2.montgomery_model())
    #print(Ea2.j_invariant())
    #print(S_B)

    
    #compute phi3
    RB = S_B
    phi2 = Ea2.isogeny(RB)
    Ea3 = phi2.codomain()
    S_B = phi2(S_B)
    #print(Ea3.montgomery_model())
    #print(Ea3.j_invariant())
    #print(S_B)


    #compute phiB
    phiB = phi2*phi1*phi0
    #print(phiB.codomain().montgomery_model())
    print("pathB =(",E.j_invariant(),")->(",Ea1.j_invariant(),")->(",Ea2.j_invariant(),")->(",Ea3.j_invariant(),")")
    PKB = (phiB.codomain(),phiB(PA),phiB(QA))
    print(PKB)
1
2
3
4
pathA =( 87*i + 190 )->( 107 )->( 344*i + 190 )->( 350*i + 65 )->( 222*i + 118 )
(Elliptic Curve defined by y^2 = x^3 + (329*i+423)*x^2 + (63*i+11)*x + (52*i+423) over Finite Field in i of size 431^2, (311*i + 218 : 289*i + 47 : 1), (108*i + 73 : 161*i + 220 : 1))
pathB =( 87*i + 190 )->( 106*i + 379 )->( 325*i + 379 )->( 344*i + 190 )
(Elliptic Curve defined by y^2 = x^3 + (329*i+423)*x^2 + (215*i+415)*x + (419*i+369) over Finite Field in i of size 431^2, (402*i + 424 : 191*i + 157 : 1), (198*i + 336 : 29*i + 287 : 1))

这里是按照论文演示的一样，将度为16、度为27的同源分别拆成4个2-isogeny和3个3-isogeny的复合，便于展示移动的路径。同时可以注意到中途的一些曲线参数和论文中的似乎并不一样，但是他们的j不变量都相同，因此在同构意义下都是同一条曲线。

在这个基础上，Alice和Bob如何交换共享密钥呢？

对于Alice来说，它只需要利用Bob公钥中的$\phi_B(E)$作为起始曲线，$\phi_B(P_A),\phi_B(Q_A)$作为新的起始点，计算出：

然后在此基础上去计算$\phi_B(E)$和$S_A’$生成的循环子群的同源，就得到$\phi_{AB}(E)$。

对于Bob也是一样，如此就可以计算出$\phi_{BA}(E)$。而两个同源最终会通过不同路径移动到同一个j不变量上，这个j不变量(或者说这个j不变量对应的同构意义下的那条曲线)就是他们的共享密钥了。

这一段可以表示成：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#part5 Alice's shared secret computation
if(1):
    E_start = PKB[0]
    SA = PKB[1] + kA*PKB[2]
    S_A = SA

    #compute phi0
    RA = 2^3*SA
    phi0 = E_start.isogeny(RA)
    Ea1 = phi0.codomain()
    S_A = phi0(S_A)
    #print(Ea1.montgomery_model())
    #print(S_A)

    
    #compute phi1
    RA = 2^2*S_A
    phi1 = Ea1.isogeny(RA)
    Ea2 = phi1.codomain()
    S_A = phi1(S_A)
    #print(Ea2.montgomery_model())
    #print(Ea2.j_invariant())
    #print(S_A)


    #compute phi2
    RA = 2*S_A
    phi2 = Ea2.isogeny(RA)
    Ea3 = phi2.codomain()
    S_A = phi2(S_A)
    #print(Ea3.montgomery_model())
    #print(Ea3.j_invariant())
    #print(S_A)


    #compute phi3
    RA = S_A
    phi3 = Ea3.isogeny(RA)
    Ea4 = phi3.codomain()
    S_A = phi3(S_A)
    #print(Ea4.montgomery_model())
    #print(Ea4.j_invariant())
    #print(S_A)

    
    #compute phiA
    phiA = phi3*phi2*phi1*phi0
    #print(phiA.codomain().montgomery_model())
    print("pathA =(",E_start.j_invariant(),")->(",Ea1.j_invariant(),")->(",Ea2.j_invariant(),")->(",Ea3.j_invariant(),")->(",Ea4.j_invariant(),")")
    shared_key_AB = Ea4.j_invariant()


#part6 Bob's shared secret computation
if(1):
    E_start = PKA[0]
    SB = PKA[1] + kB*PKA[2]
    S_B = SB

    #compute phi0
    RB = 3^2*SB
    phi0 = E_start.isogeny(RB)
    Ea1 = phi0.codomain()
    S_B = phi0(S_B)
    #print(Ea1.montgomery_model())
    #print(S_B)

    
    #compute phi1
    RB = 3*S_B
    phi1 = Ea1.isogeny(RB)
    Ea2 = phi1.codomain()
    S_B = phi1(S_B)
    #print(Ea2.montgomery_model())
    #print(Ea2.j_invariant())
    #print(S_B)

    
    #compute phi3
    RB = S_B
    phi2 = Ea2.isogeny(RB)
    Ea3 = phi2.codomain()
    S_B = phi2(S_B)
    #print(Ea3.montgomery_model())
    #print(Ea3.j_invariant())
    #print(S_B)


    #compute phiB
    phiB = phi2*phi1*phi0
    #print(phiB.codomain().montgomery_model())
    print("pathB =(",E_start.j_invariant(),")->(",Ea1.j_invariant(),")->(",Ea2.j_invariant(),")->(",Ea3.j_invariant(),")")
    shared_key_BA = Ea3.j_invariant()

print(shared_key_AB == shared_key_BA)
1
2
3
pathA =( 344*i + 190 )->( 364*i + 304 )->( 67 )->( 242 )->( 234 )
pathB =( 222*i + 118 )->( 299*i + 315 )->( 61 )->( 234 )
True

如此就复现出了论文里的简单SIDH示例。

而上述写法为了展示出路径所以采用了多个同源复合的写法，比较冗长。事实上一个普遍的SIDH可以写为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
from random import randint

#part1 construct supersingular ECC on F_p2
a = 4
b = 3
p = 2^a*3^b - 1
F.<i> = GF(p^2, modulus = x**2 + 1)
a0 = 329*i+423
E = EllipticCurve(F,[0,a0,0,1,0])


#part2 Alice's and Bob's public points
PA = E(0)
while (2^(a-1))*PA == 0:
    PA = 3^b * E.random_point()
QA = PA
while PA.weil_pairing(QA, 2^a)^(2^(a-1)) == 1:
    QA = 3^b * E.random_point()
#print(PA,QA)

PB = E(0)
while (3^(b-1))*PB == 0:
    PB = 2^a * E.random_point()
QB = PB
while PB.weil_pairing(QB, 3^b)^(3^(b-1)) == 1:
    QB = 2^a * E.random_point()
#print(PB,QB)


#part3 Alice choose secret kA and gen Alice's public key
kA = randint(0, 2^a-1)
SA = PA + kA * QA
phiA = E.isogeny(SA)
EA, phiA_PB, phiA_QB = phiA.codomain(), phiA(PB), phiA(QB)
PKA = (EA, phiA_PB, phiA_QB)


#part4 Bob choose secret kB and gen Bob's public key
kB = randint(0, 3^b-1)
SB = PB + kB * QB
phiB = E.isogeny(SB)
EB, phiB_PA, phiB_QA = phiB.codomain(), phiB(PA), phiB(QA)
PKB = (EB, phiB_PA, phiB_QA)


#part5 Alice's shared secret computation
E_start = PKB[0]
SA_ = PKB[1] + kA*PKB[2]
EAB = E_start.isogeny(SA_).codomain()


#part6 Bob's shared secret computation
E_start = PKA[0]
SB_ = PKA[1] + kB*PKA[2]
EBA = E_start.isogeny(SB_).codomain()


print(EAB.j_invariant() == EBA.j_invariant())


困难性

SIDH的困难性在于，当有限域较大时，给定一个曲线E，以及其同源映射后的曲线EA，难以求解出他们之间的同源$\phi_A$。同理也就求不出Alice和Bob选择的秘密私钥kA和kB，以及对应的子群的生成元SA和SB了。



总结

到这里对SIDH的基本概念就简单介绍完了，需要注意的是SIDH在两年前已经被宣布完全破解，并且github上就有现成的attack可以使用：

GiacomoPope/Castryck-Decru-SageMath: A SageMath implementation of the Castryck-Decru Key Recovery attack on SIDH (github.com)

所以除了见过的中间相遇(N1CTF junior的iev@l，以及seetf的isogeny maze)，以及直接利用这个attack恢复密钥(cryptoctf的shevid)外，我还并没有想到可以怎么设计题目。

总而言之这篇学习笔记囿于我自身抽代水平等各种不足，以及并没有见过很多isogeny的相关题目，所以写的其实相当浅显，也可能会存在不少错误。本意是想记录自己的学习过程，并分享出来抛砖引玉，欢迎各位师傅与我交流。