糖醋小鸡块的blog
0%

2023-SICTF-#Round2-wp-crypto

发表于 更新于 分类于 Valine：

这次比赛Crypto难度比较基础，手速快才是硬道理。

Rank：2

image-20230911152911874



[签到]古典大杂烩

题目描述：

1
请尝试解密它。

题目：

1
🐩👃🐪🐼👅🐯🐩👈👇👭👟👝🐺🐭👉👙👤👋👚🐪🐫👍👢👮👱🐼👢👨👠👭🐽🐰🐻👚👂👧👠👥👛👮👯👮👬🐾👐👛👌👚👞🐨👏👉👆🐿👆👘👇🐺👦🐸👃🐭👟👑👪👃👁🐻🐻👜🐧👇👊🐧🐾🐼👇🐫🐺👐👆👪🐼👋👌👧🐻👐🐩🐺👥🐽👋👉🐰👎👠👠👣🐧🐫👧🐭👢🐯👑👑🐮👂👏🐻👥👚🐮👋👬👌👥👁👣👅👧👯👦👌👌👍👠👌🐽👉👃👊🐫👉🐨🐮👩👆🐪🐯👘👏👏🐼👩👍👊👍👡👀👰👋👣👨👧👍👜👐👛🐮👘👅👠🐿👂👰👄👈👝👠👤👃👛👘🐭👅👱👆👬👫👥👆🐽👁👐👥👊👇👉👊👩👌👭🐫🐫👬👱🐯👇🐺👁👞👑👙🐮👜👋👘👪👩👚👦👨👀👩👐👉👃🐾👥👀🐫👝👍🐩🐧👰👆👇👨🐪👃🐭👦🐫👱

第一层很明显是base100，之后的每一层像哪个base用哪个解密即可：

1、 base100：

1
2L3EN82QPvhfC6RbmTc34VkwzEkqivF9DcKpindwxwuGYdUcg1XROHOaPCoAL6hZsLJDDe0PS0GEP4CYOsETUpDY2CnFTR9Wiil04p6k8ZZ7KXDnc7TuUnJlNpxoUUViUFRLS4R17rO38aXXErVSVjIyTlqpVeYd7aNiHKyMQfimLda6NzOutnOFJYnSPRSrUv44uz8PCJgZb7eTasrcoqIrYRLGnI4fV20yOPq3L6o4z

2、 base62：

1
UlhoYUdxZTdaY1FCbXFyaWl5S0ZKaW4yN2ZiWkpTZHhOd2hBVk1wNzRvUWE0VWs2RXVqTlpkTHNvYVpxNHRMUDd3dXk4OGJiSlhlTGJnN2dxR2RkTm15dGs1S1RGdlk3TmpRR0wzenFrQ3BCM3lmUTFTUkY0OU13Z0JjZkFxWjFhNng=

3、base64：

1
RXhaGqe7ZcQBmqriiyKFJin27fbZJSdxNwhAVMp74oQa4Uk6EujNZdLsoaZq4tLP7wuy88bbJXeLbg7gqGddNmytk5KTFvY7NjQGL3zqkCpB3yfQ1SRF49MwgBcfAqZ1a6x

4、 base58：

1
G53XC4LIK5DWQ53UIFSGCUTCJFCGM4DSM5UXOYTILBUXU6TXJ5SUUT2DONHTQZ3GJNCFSUDINRXE6MTEINUXOQLVLI4VU===

5、 base32：

1
7wqqhWGhwtAdaRbIDfprgiwbhXizzwOeJOCsO8gfKDYPhlnO2dCiwAuZ9Z

6、base62：

1
SICTF{fe853b49-8730-462e-86f5-fc8e9789f077}

flag：

SICTF{fe853b49-8730-462e-86f5-fc8e9789f077}



Radio

题目描述：

1
树木新开发了一个加密系统，这个系统会把他的秘密加密很多次然后发送给不同的用户，你能找到其中的漏洞吗？

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Util.number import *
from flag import flag
m = bytes_to_long(flag)
p = getPrime(1024)
q = getPrime(1024)
n1 = p * q
p = getPrime(1024)
q = getPrime(1024)
n2 = p * q
p = getPrime(1024)
q = getPrime(1024)
n3 = p * q
e = 17
c1 = pow(m,e,n1)
c2 = pow(m,e,n2)
c3 = pow(m,e,n3)
print("n1 =",n1)
print("n2 =",n2)
print("n3 =",n3)
print("c1 =",c1)
print("c2 =",c2)
print("c3 =",c3)

经典的广播攻击，思路就是使用中国剩余定理得到$\quad mod \; (n1n2n3)\quad$下的$\quad m^{17}\quad$，再开17次方根即可。

exp.py：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sympy.ntheory.modular import crt 
from gmpy2 import iroot
from Crypto.Util.number import *

n1 = 
n2 = 
n3 = 
c1 = 
c2 = 
c3 = 
e = 17

n = [n1,n2,n3]
c = [c1,c2,c3]
M = crt(n,c)[0]

print(long_to_bytes(iroot(M,17)[0]))

flag：

SICTF{fdc0afb5-1c81-46b9-a28a-241f5f64419d}



MingTianPao

题目描述：

1
这个题目名充分表现了作者由于学CTF导致吃不上饭，明天就打算跑路的心里想法。

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import binascii
from Crypto.Util.strxor import strxor
from secret import flag, message
# message is a Classic English Story

for i in range(10):
    tmp = (message[i*30:(i+1)*30].encode())
    print(binascii.hexlify(strxor(tmp,flag)).decode())

# 1f2037202a1e6d06353b61263d050a0538493b3018544e14171d2b1c4218
# 3769373b66142f31297f291126410e042b01162d59103a0c005221075013
# 37242c202e1e3f743c36371130410c1e2b491a31574406014505291a550e
# 7f6922742e1a213270372e01264105193004532b1f554e120c1e2a145618
# 7d69143c23156d18392b35183141310e3b49213613590003453a291a555d
# 36273731341e297424372454230e0c0f2c49127f005f020245112718545d
# 26396320295b2531227161273c04430f360d533118444e0f0b1d31554615
# 323d6335660c24373b3a2554350f0a063e05533712101905165e66145f19
# 733e222766152220703e27063508074b300f53371e5d40444735291a555d
# 37283a7432146d2d3f2a6d541808171f330c530d12544e360c162f1b565d

很明确的一个Many-Time-Pad，也对应了题目名字MTP，预期来说应该是上一个知名MTP脚本求解。

但是其实完全不需要，因为题目给了这样一个提示：

1
# message is a Classic English Story

我们又有flag的前六个字符：SICTF{

那么拿去异或一下就有：

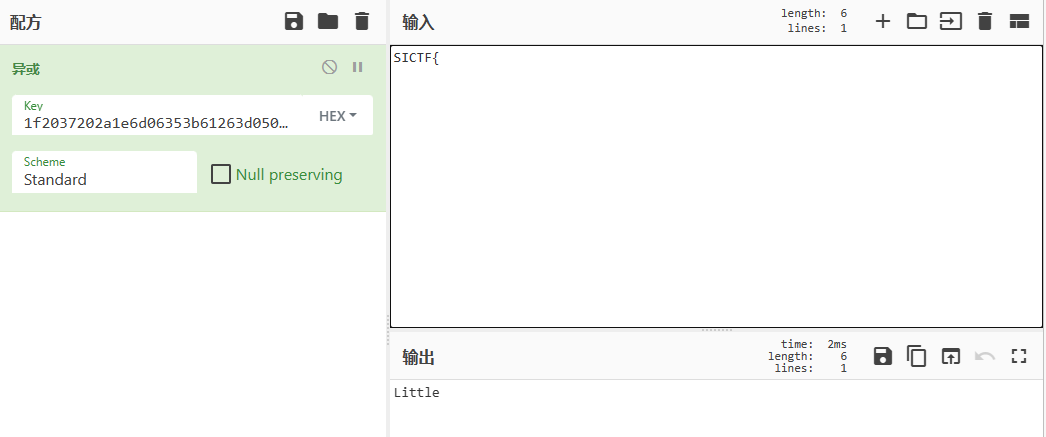
image-20230908224043439

合理猜测这是一个Little开头的英语故事，那么由于异或的可逆性，直接把密文搬上明文的位置，来试几个：

Little Prince（小王子）：

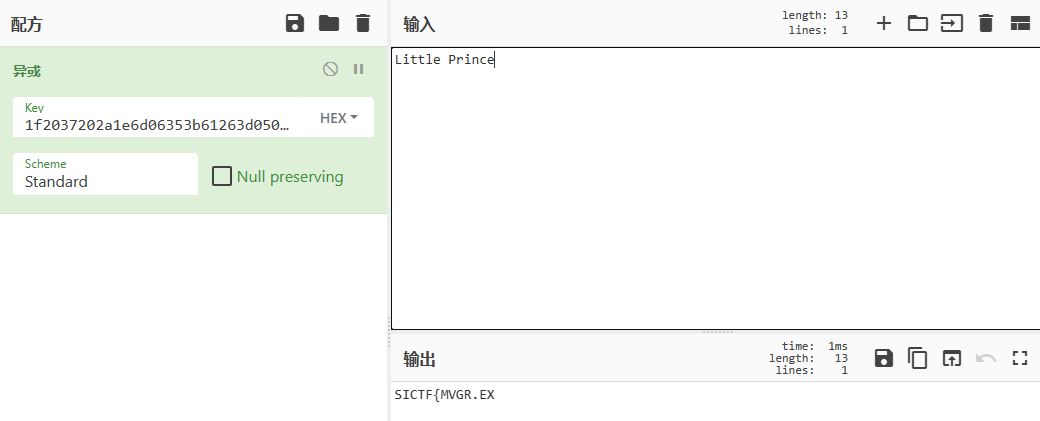
image-20230908224223829

不太对，换一个，Little Red Riding Hood：

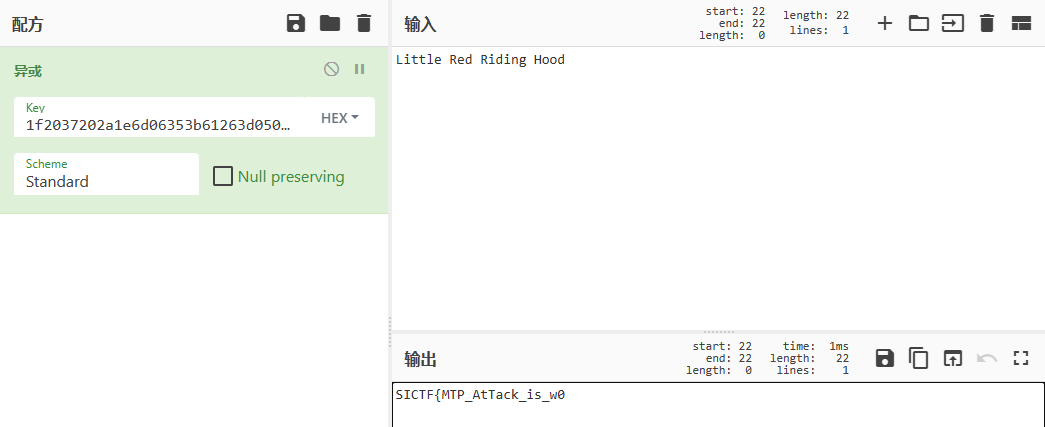
image-20230908224336581

这就成了，又可以看出flag串后面应该是wonderful的变形，那么再把flag串搬上来逐个尝试即可：（因为可以变的其实就大小写、以及形近数字，一个字符一个字符增加，试几次就出来了）：

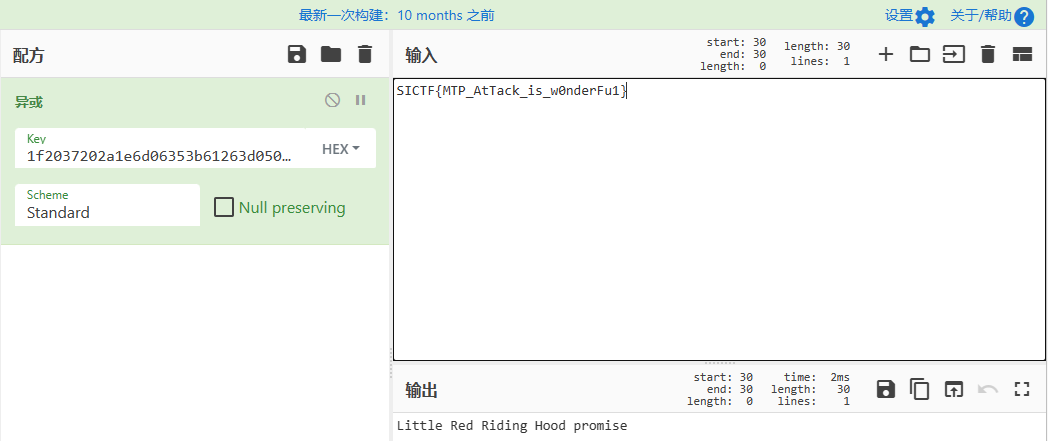
image-20230908224509359

flag：

SICTF{MTP_AtTack_is_w0nderFu1}



Easy_CopperSmith

题目描述：

1
你知道CopperSmith吗？

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from Crypto.Util.number import *
from flag import flag
p = getPrime(512)
q = getPrime(512)
n = p * q
e = 65537
leak = p >> 230
m = bytes_to_long(flag)
c = pow(m,e,n)
print(n)
print(leak)
print(c)
'''
114007680041157617250208809154392208683967639953423906669116998085115503737001019559692895227927818755160444076128820965038044269092587109196557720941716578025622244634385547194563001079609897387390680250570961313174656874665690193604984942452581886657386063927035039087208310041149977622001887997061312418381
6833525680083767201563383553257365403889275861180069149272377788671845720921410137177
87627846271126693177889082381507430884663777705438987267317070845965070209704910716182088690758208915234427170455157948022843849997441546596567189456637997191173043345521331111329110083529853409188141263211030032553825858341099759209550785745319223409181813931086979471131074015406202979668575990074985441810
'''

直白的p高位泄漏，直接解密即可。

exp.ipynb：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from Crypto.Util.number import *

n = 114007680041157617250208809154392208683967639953423906669116998085115503737001019559692895227927818755160444076128820965038044269092587109196557720941716578025622244634385547194563001079609897387390680250570961313174656874665690193604984942452581886657386063927035039087208310041149977622001887997061312418381
p4 = 6833525680083767201563383553257365403889275861180069149272377788671845720921410137177
c = 87627846271126693177889082381507430884663777705438987267317070845965070209704910716182088690758208915234427170455157948022843849997441546596567189456637997191173043345521331111329110083529853409188141263211030032553825858341099759209550785745319223409181813931086979471131074015406202979668575990074985441810
e =  65537

pbits = 512
kbits=pbits - p4.nbits()
p4 = p4 << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p4
roots = f.small_roots(X=2^kbits,beta=0.4,epsilon = 0.01)
# 经过以上一些函数处理后，n和p已经被转化为10进制
if roots:
    p= p4 + int(roots[0])
    q = n//p
d = inverse(e,(p-1)*(q-1))
m = pow(c,d,n)
print(long_to_bytes(int(m)))

flag：

SICTF{3f9366ed-b8e4-412f-bbd0-62616a24115c}



签到题来咯！

题目描述：

1
签到题来咯！

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from secret import flag
from  Crypto.Util.number import *

m = bytes_to_long(flag)
p = getPrime(1024)
q = getPrime(1024)
e = getPrime(10)
n = p*q
c1 = pow(114*m+2333,e,n)
c2 = pow(514*m+4555,e,n)
print(f'n = {n}')
print(f'c1 = {c1}')
print(f'c2 = {c2}')
'''
n = 18993579800590288733556762316465854395650778003397512624355925069287661487515652428099677335464809283955351330659278915073219733930542167360381688856732762552737791137784222098296804826261681852699742456526979985201331982720936091963830799430264680941164508709453794113576607749669278887105809727027129736803614327631979056934906547015919204770702496676692691248702461766117271815398943842909579917102217310779431999448597899109808086655029624478062317317442297276087073653945439820988375066353157221370129064423613949039895822016206336117081475698987326594199181180346821431242733826487765566154350269651592993856883
c1 = 3089900890429368903963127778258893993015616003863275300568951378177309984878857933740319974151823410060583527905656182419531008417050246901514691111335764182779077027419410717272164998075313101695833565450587029584857433998627248705518025411896438130004108810308599666206694770859843696952378804678690327442746359836105117371144846629293505396610982407985241783168161504309420302314102538231774470927864959064261347913286659384383565379900391857812482728653358741387072374314243068833590379370244368317200796927931678203916569721211768082289529948017340699194622234734381555103898784827642197721866114583358940604520
c2 = 6062491672599671503583327431533992487890060173533816222838721749216161789662841049274959778509684968479022417053571624473283543736981267659104310293237792925201009775193492423025040929132360886500863823523629213703533794348606076463773478200331006341206053010168741302440409050344170767489936681627020501853981450212305108039373119567034948781143698613084550376070802084805644270376620484786155554275798939105737707005991882264123315436368611647275530607811665999620394422672764116158492214128572456571553281799359243174598812137554860109807481900330449364878168308833006964726761878461761560543284533578701661413931
'''

经典的明文相关消息攻击，略做了一点变种。思路如下，列出两个多项式：

又因为明文m显然是两个模多项式的根，因此两个模多项式有公因子：

因此构造出模n环下的两个多项式，并求公因式即可。至于e是多少，仅需要在指定范围内爆破一下就可以。

exp.ipynb：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from gmpy2 import *
from Crypto.Util.number import *

n = 18993579800590288733556762316465854395650778003397512624355925069287661487515652428099677335464809283955351330659278915073219733930542167360381688856732762552737791137784222098296804826261681852699742456526979985201331982720936091963830799430264680941164508709453794113576607749669278887105809727027129736803614327631979056934906547015919204770702496676692691248702461766117271815398943842909579917102217310779431999448597899109808086655029624478062317317442297276087073653945439820988375066353157221370129064423613949039895822016206336117081475698987326594199181180346821431242733826487765566154350269651592993856883
c1 = 3089900890429368903963127778258893993015616003863275300568951378177309984878857933740319974151823410060583527905656182419531008417050246901514691111335764182779077027419410717272164998075313101695833565450587029584857433998627248705518025411896438130004108810308599666206694770859843696952378804678690327442746359836105117371144846629293505396610982407985241783168161504309420302314102538231774470927864959064261347913286659384383565379900391857812482728653358741387072374314243068833590379370244368317200796927931678203916569721211768082289529948017340699194622234734381555103898784827642197721866114583358940604520
c2 = 6062491672599671503583327431533992487890060173533816222838721749216161789662841049274959778509684968479022417053571624473283543736981267659104310293237792925201009775193492423025040929132360886500863823523629213703533794348606076463773478200331006341206053010168741302440409050344170767489936681627020501853981450212305108039373119567034948781143698613084550376070802084805644270376620484786155554275798939105737707005991882264123315436368611647275530607811665999620394422672764116158492214128572456571553281799359243174598812137554860109807481900330449364878168308833006964726761878461761560543284533578701661413931
a1 = 114
b1 = 2333
a2 = 514
b2 = 4555
elist = [521,523,541,547,557,563,569,571,577,587,593,599,601,607,613,617,619,631,641,643,647,653,659,661,673,677,683,691,701,709,719,727,733,739,743,751,757,761,769,773,787,797,809,811,821,823,827,829,839,853,857,859,863,877,881,883,887,907,911,919,929,937,941,947,953,967,971,977,983,991,997,1009,1013,1019,1021]
def attack(c1, c2, e, n):
    PR.<x>=PolynomialRing(Zmod(n))
    g1 = (a1*x + b1)^e - c1
    g2 = (a2*x + b2)^e - c2

    def gcd(g1, g2):
        while g2:
            g1, g2 = g2, g1 % g2
        return g1.monic()
    return -gcd(g1, g2)[0]

for e in elist:
    m1 = attack(c1, c2, e, n)
    if(b"SICTF" in long_to_bytes(int(m1))):
        flag = long_to_bytes(int(m1))
        print(flag)

flag：

SICTF{hhh!!franklin_reiter_is_easy}



small_e

题目描述：

1
这个低加密指数攻击为什么打不出来哇？是不是题有问题捏？差评！

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import libnum
from Crypto.Util.number import *
import uuid
flag="SICTF{"+str(uuid.uuid4())+"}"
m=libnum.s2n(flag)
p=getPrime(1024)
q=getPrime(1024)
n=p*q
e=3
c=pow(m,e,n)
m1=((m>>60)<<60)
print("n=",n)
print("e=",e)
print("c=",c)
print("((m>>60)<<60)=",m1)
print(flag)
'''
n= 23407088262641313744603678186127228163189328033499381357614318160776774708961658114505773173784501557046914457908828086210961235530240151825359345210845219656000760996670856300710703016947799649686427460688236465568188205550456293373157997725204643414082796492333552579250010906010553831060540937802882205118399938918764313169385349293602085310111289583058965780887097301702677087443291977479125263301000328313103296364864396361278863921717374909215078711198899810620522933994481419395021233240234478331179727351050575360886334237633420906629984625441302945112631166021776379103081857393866576659121443879590011160797
e= 3
c= 1584727211980974717747362694412040878682966138197627512650829607105625096823456063149392973232737929737200028676411430124019573130595696272668927725536797627059576270068695792221537212669276826952363636924278717182163166234322320044764324434683614360641636360301452618063418349310497430566465329766916213742181
((m>>60)<<60)= 11658736990073967239197168945911788935424691658202162501032766529463315401599017877851823976178979438592
'''

已知明文高位攻击，直接上脚本。

exp.ipynb：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Util.number import *

n= 23407088262641313744603678186127228163189328033499381357614318160776774708961658114505773173784501557046914457908828086210961235530240151825359345210845219656000760996670856300710703016947799649686427460688236465568188205550456293373157997725204643414082796492333552579250010906010553831060540937802882205118399938918764313169385349293602085310111289583058965780887097301702677087443291977479125263301000328313103296364864396361278863921717374909215078711198899810620522933994481419395021233240234478331179727351050575360886334237633420906629984625441302945112631166021776379103081857393866576659121443879590011160797
e= 3
c= 1584727211980974717747362694412040878682966138197627512650829607105625096823456063149392973232737929737200028676411430124019573130595696272668927725536797627059576270068695792221537212669276826952363636924278717182163166234322320044764324434683614360641636360301452618063418349310497430566465329766916213742181
m= 11658736990073967239197168945911788935424691658202162501032766529463315401599017877851823976178979438592

PR.<x> = PolynomialRing(Zmod(n))
f = (m + x)^e - c
f = f.monic()
roots = f.small_roots()

m = m + int(roots[0])
print(long_to_bytes(m))

flag：

SICTF{2ca8e589-4a31-4909-80f0-9ecfc8f8cb37}



easy_math

题目描述：

1
其实数学很简单辣！

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from secret import flag
from  Crypto.Util.number import *

m = bytes_to_long(flag)
p = getPrime(512)
q = getPrime(512)
n = p * q
e = 65537
hint1 = getPrime(13)*p+getPrime(256)*q
hint2 = getPrime(13)*p+getPrime(256)*q
c = pow(m,e,n)
print(f'n = {n}')
print(f'hint1 = {hint1}')
print(f'hint2 = {hint2}')
print(f'c = {c}')

'''
n = 68123067052840097285002963401518347625939222208495512245264898037784706226045178539672509359795737570458454279990340789711761542570505016930986418403583534761200927746744298082254959321108829717070206277856970403191060311901559017372393931121345743640657503994132925993800497309703877076541759570410784984067
hint1 = 564294243979930441832363430202216879765636227726919016842676871868826273613344463155168512928428069316237289920953421495330355385445649203238665802121198919543532254290185502622234014832349396422316629991217252686524462096711723580
hint2 = 484307144682854466149980416084532076579378210225500554261260145338511061452958092407101769145891750844383042274498826787696953308289632616886162073232218214504005935332891893378072083589751354946391146889055039887781077066257013110
c = 57751903193610662622957432730720223801836323458721550133101805763463060486486266309568004721657732742899781400754207249733137375171400440423755473421971160000575072519031824740691618617905549725344323721903857290320737224300672847773455169809689188843070599176261204013341324705808617411345132933937680951713
'''

注意到hint1、hint2的生成过程：

而p前的系数a1、a2很小，因此可以先打印出所有13比特的素数存在一张表内，作为a1、a2的所有可能取值，然后如下操作：

与n求gcd即可得到q，之后进行RSA解密即可。

exp.py：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from  Crypto.Util.number import *

n = 68123067052840097285002963401518347625939222208495512245264898037784706226045178539672509359795737570458454279990340789711761542570505016930986418403583534761200927746744298082254959321108829717070206277856970403191060311901559017372393931121345743640657503994132925993800497309703877076541759570410784984067
hint1 = 564294243979930441832363430202216879765636227726919016842676871868826273613344463155168512928428069316237289920953421495330355385445649203238665802121198919543532254290185502622234014832349396422316629991217252686524462096711723580
hint2 = 484307144682854466149980416084532076579378210225500554261260145338511061452958092407101769145891750844383042274498826787696953308289632616886162073232218214504005935332891893378072083589751354946391146889055039887781077066257013110
c = 57751903193610662622957432730720223801836323458721550133101805763463060486486266309568004721657732742899781400754207249733137375171400440423755473421971160000575072519031824740691618617905549725344323721903857290320737224300672847773455169809689188843070599176261204013341324705808617411345132933937680951713
e = 65537
primelist = [i for i in range(2**12,2**13) if isPrime(i)]
for i in primelist:
    for j in primelist:
        if(GCD(hint1*i - hint2*j,n) != 1):
            q = GCD(hint1*i - hint2*j,n)
p = n//q
d = inverse(e,(p-1)*(q-1))
m = pow(c,d,n)
print(long_to_bytes(m))

flag：

SICTF{452aebb6-9c16-441a-ac42-fc608bf6063f}



总结

越熟练手速就会越快，继续努力！