期末总算过去了,终于有时间来更新更新已经过去了大半个月的CryptoCTF。这次比赛和认识的一些师傅一起组了个小队cyberCryer,最后拿到了第二名:
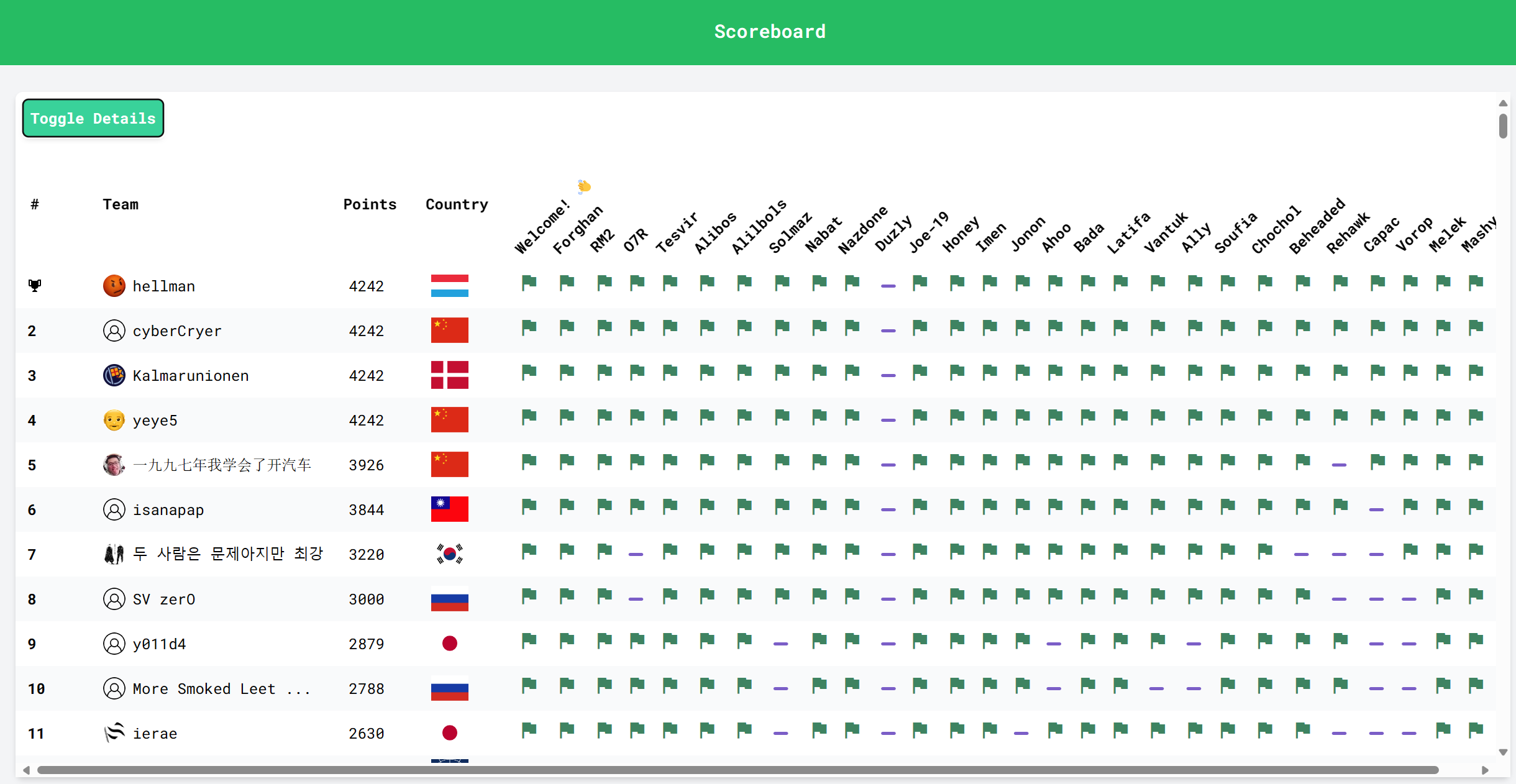
虽然说这次比赛的一些题目实在有点无力吐槽,但是比赛中途大家一起加班加点肝题的乐趣是实打实的,再次感谢cyberCryer的各位师傅。( つ•̀ω•́)つ
由于大家一起在做题,所以部分题目的wp是我赛后复现的,并不一定是做题的师傅的思路。同时我也记录了一些比赛中的有趣的动态,留作纪念。
队伍其他师傅的wp指路:
Zima:CRYPTOCTF2024(part1) | Zimablue’ Blog
……
Warm-up
Welcome! 👋(367 solves , 27 pts)
题目描述:
1 | We are excited that you will be participating in 6th CryptoCTF, an engaging online event focused on challenging and improving your cryptography abilities. You'll have the opportunity to dive into the captivating realm of ciphers, codes, and modern cryptosystems. 💪 ⚡ 💥 🔥 |
直接交:
1 | flag: CCTF{Harn3sS_Y0ur_CrYptO9rAphy_Pr0wEs5_💪_⚡_💥_🔥!} |
Easy
Alibos(181 solves , 36 pts)
题目描述:
1 | Alibos, a classic cryptographic algorithm, is designed to safeguard non-sensitive data, providing a reliable solution for routine information protection. |
题目:
1 | #!/usr/bin/env python3 |
output.txt:
1 | pkey = 8582435512564229286688465405009040056856016872134514945016805951785759509953023638490767572236748566493023965794194297026085882082781147026501124183913218900918532638964014591302221504335115379744625749001902791287122243760312557423006862735120339132655680911213722073949690947638446354528576541717311700749946777 |
题目含有一个未知的量d,利用这个d生成了随机的skey和pkey,然后按如下方式加密:
然而仔细看的话会发现加密式子里的d实际上是pkey的字符串长度,所以可以直接解出m然后去掉pad就行。
exp:
1 | from Crypto.Util.number import * |
Beheaded(32 solves , 131 pts)
题目描述:
1 | The beheaded flags have had their headers removed, making them encrypted. Can a living entity truly survive without a head? |
题目:
1 |
|
题目将flag串写在图片上,然后对这张图片进行ECB加密,最后得到密文文件。
原理的话其实并不复杂,对于一张图片来说,其分为了很多色块,而由于是ECB加密,所以对于相同的色块(也就是背景色),其密文也一定是相同的,而这也说明一点——不是背景色块密文的地方,就一定有内容。所以可以统计密文来大致还原轮廓。而对于这个题目来讲,其就是把文字写在图片上的图片,所以还原轮廓就等于还原flag。
不过具体操作上应该还是挺有讲究,比如ppm格式、加密分组怎么对应色块等我都不是很清楚,但@Zima正好了解这些,就用了一个工具直接把他梭掉了。
Mashy(68 solves , 71 pts)
题目描述:
1 | Mashy may seem like a simple cracking task, but you'll need to open your eyes to identify the right things to crack. |
题目:
1 | #!/usr/bin/env python3 |
这个题总的来说要完成七轮挑战,每一轮都需要输入两个十六进制串d1、d2,靶机会计算他们的md5值h1、h2,这些值如果满足以下要求就可以通过本轮挑战:
d1不等于d2
d1、d2之前没有输入过
$d_1 \oplus d_2$的md5值不为’ae09d7510659ca40eda3e45ca70e9606’
$h_1 \oplus h_2 \oplus sh$的值为’a483b30944cbf762d4a3afc154aad825’,其中sh为(salt未知):
1
sh = md5(salt).digest()
怎么看都想不通要干什么,首先这个sh是不知道的,所以也就不知道h1异或h2到底要满足什么东西,只知道需要是一个定值;其次就是d1异或d2的md5值也不知道是什么,不过这个还好,仅仅是要求不为多少,很容易就能做到。
一头雾水的时候发现这个题解数蹭蹭涨,所以盲猜应该只是个md5的碰撞,也就是让d1、d2不等的情况下h1、h2相等,这也就意味着sh就是’a483b30944cbf762d4a3afc154aad825’。上在线网站生成几组前缀碰撞然后交互就好:
MD5 在线碰撞 - 百川在线工具箱 (chaitin.cn)
exp:
1 | from pwn import * |
Medium
Ahoo(29 solves , 142 pts)
题目描述:
1 | Ahoo, the swiftest and most graceful gazelle in Iran, is renowned for her unmatched beauty and uncanny ability to evade even the most cunning traps. |
没有附件,题目的题意是:
- 给定一个正整数n(大概在几千这个数量级),要求给出最小的正整数c,使得t=nc的汉明重量最小
最开始当然只想到爆破,但是实际效果来说,爆破能够到的范围太小了,很容易出错。之后@yolbby想了一个用格的方法,差不多是:
- 把t看作是一个背包,背包里的值是2^k,造格规约出来的短向量就是汉明重量比较小的。
这样能找到的c的范围就和格的维数直接相关,比如格大小为256,那么格能找到的最优解就是2^256以内的c,肯定是比爆破要好的
然后再单独处理一下汉明重量可能为2的情况。若汉明重量是2,那么可以写成t = 2^r(2^s+1) = nc,其实也就可以等价成c=2^s+1/n,所以可以再单独找一下比较大的c,就可以大于2^256。
造格似乎有点不太好理解,其实就是利用这个等式:
既然要让t汉明重量较小,所以如果把他用二进制表示的话,系数是很稀疏的,也就是如果写成:
那么ai应该很多0,只有极少数是1。
那么把等式移一下项就变成了:
所以就可以造格。
256这个数完全是自己选择的,要平衡一下能找到的范围和格规约的时间才行,选择256代表着可以找到2^256以内的t,大一点查找范围自然也大一些,但是规约就会慢。
上手实现了一下发现确实行,不过仍然有失败的可能,由于要通过20轮,优化了很久都没搞定,最多挂到十五十六轮的样子,所以这肯定不是通法。不过还是把solver发上来留作纪念:
1 | from pwn import * |
怎么都优化不出来的时候@leukocyte登场,他看出这实际上是一个关于同余最短路的算法题,所以直接交给他做,果然很快就秒了。但我的算法功底很烂,所以应该理解不了。
赛后看春哥的wp发现说可以求出前几项之后上OEIS查数列,就能查到关于通解的论文,以及前10000项的结果,所以可以查表然后发回去。
Alilbols(59 solves , 80 pts)
题目描述:
1 | Alilbols, a modified version of the Alibos cryptographic algorithm, offers enhanced security features to protect sensitive and confidential data. |
题目:
1 | #!/usr/bin/env python3 |
output.txt:
1 | h = 1051643987107349427988807326909852110640860009433515828832892541964729933410444984350917250524103015414239941369074041041830326426044333499878031164851095096864048639115431370526747014210332286314344073411522846701723463410585601251886732229726828022089809603850477551571014006202841406236367999378786782206165205893353928598469661871284779486855440579818275314024966224282757807716013799903830828885606714972634243850947534165272668985513949964901606268939300116019465522042467054120201087606016018354238401711720121586874288767235317479748890350702705575809130664969776549574720593740409234863974057904204809404816059921579771581800937241591669455683460570640868196509926763901079838233646036933530095891316054589051458146768287967886035091641162494322987627448810201550901588438560433001422233269632915351406169253963308421081459981594969405377353502889363324282815864766827664453823780238352371809048289845094882346227809082005375092441877966603138648719670349093616548820955566204871333952902983753935678447080673827214244142614295192263451840766771122229866931492260663320087497820892824540996643905125018452302747847009 |
题目仍然是有一个未知的量d,利用这个d先生成了一组密钥pkey和skey,然后再用公钥pkey加密m得到密文c。
那么就先看这个genkey,其步骤是:
生成f、g,满足:
生成q,满足$q = 4 \cdot 10^{2d}$
计算h:
得到公钥(d,h),私钥(f,g)
之后看encrypt:
q还是上面那个q
取一个随机数r,$r \in (1,\frac{10^d}{2})$
计算密文c:
给出h、c,要求还原m。
可以看出他的genkey其实是一个ntru,所以有q的情况下可以造格得到f、g。然而问题在于题目没有给出q也没有给出d,但是可以发现c、h都是模q下的量,所以q应该会略大于c、h,因此可以简单在范围附近爆破一下d,检查一下规约出的f、g是否合理就行。
得到f、g之后就等于得到了私钥,之后类似ntru去解密。由于有:
所以:
和ntru一样,由于各个数字数量级均有限制,所以整个式子不模q也是成立的,也就是:
所以有:
然后再在f+g下对f求逆就可以得到m。
exp:
1 | from Crypto.Util.number import * |
Ally(22 solves , 174 pts)
题目描述:
1 | Ally enjoys the challenge of solving Diophantine equations, so help them tackle this latest complex equation as well. |
题目:
1 | #!/usr/bin/env python3 |
题目共19轮挑战,每一轮挑战需要满足:
输入一个指定大小的素数p
给出下面丢番图方程的一个正整数解:
赛中的时候研究这个研究了好久,既没有搜到啥论文,也没想到能怎么自己构造。最后@yolbby给出了一个巧妙的思路:
exp:
1 | from pwn import * |
Bada(51 solves , 90 pts)
题目描述:
1 | The Bada equation contains an undetermined function. By closely examining how this equation behaves, you may be able to discover the concealed flag. |
依然没有附件,题目内容是:
存在一个未知的函数f,满足:
其中所有值都是整数,靶机会给出两个值:
要求求出x,y。
可以看出,从(1,1)到(x,y)的迭代过程完全可以看作是两个不同的等差数列,也就是:
而这两个等差数列又显然可以合成一个等差数列,也就是:
用求和公式就是:
记:
所以有:
然后交互过程中又发现了一个事情,那就是d总是一个素数,所以就很好办了,要使上式成立就只能:
然后解方程就可以得到x、y了——然而发回去不对。
当时可能正是夜里三四点钟,@Zima看了这题过后死活没看出解法哪里有问题,就叫我来;我看了看也死活没看出问题,就拉来了@yolbby;结果他也没看出来解法问题在哪,三脸懵逼。
第二天早上@hash-hash起来之后就把他解掉了,看了看思路发现说其实上面的式子还有一个可能就是:
而这样去解方程再发回去就正确了,只能说他的check逻辑不是太对(估计是直接判断是否和第二种这个解相等)。
Duzly(0 solves , 500 pts)
题目描述:
1 | Duzly is a straightforward hash function design based on congruence relationships over a prime number modulus. |
题目:
1 | #!/usr/bin/env sage |
题目不长,但是够狠。加密流程为:
生成一个长度为6的随机列表C,第一个值是1,其他均为0-p的随机数
将flag首位进行两段长度未知的随机填充
将flag切分为长度为8的多个分组
对每个分组mi,进行如下加密得到对应密文ci:
由于update里给出了C,所以这其实是一个关于mi的单变量方程,所以自然想到直接求根,然而这个多项式度是$2^{24}+17$,实在太大了,根本建不出来,所以要想下怎么降次。但是模数p是一个非常正常的素数(也就是longlong型的最大素数),2^24虽然大,但完全不会是某个元素的阶,所以消不掉。
一筹莫展的时候想了点歪点子,首先可以知道,flag虽然在首尾进行了填充,但是”CCTF{“这五个字符仍然一定在里面。又因为八个字符八个字符分了组,所以这个flag头可能有如下八种切分方式:
1 | CCTF{ + YYY |
其中,X代表纯随机字符,Y代表可见字符。可以看出,八种情况中,只有5、6两组复杂度稍大,其他的情况复杂度都不算特别高,可以进行爆破。而期望是这样:如果得到了正确的flag头的内容,比如”CCTF{i_lo”这种,就可以合理猜测下一个分组的是ve开头,从而连蒙带猜往后一个分组一个分组爆。
然而事与愿违,我一开始密文读取方式错了,导致zima师傅写的c++的多进程爆破完全就没用对数据,自然也没结果。时间又很紧张,所以最后没有搞出来flag头,自然也就不存在往后的连蒙带猜了。
赛后看discord的讨论,突然反应过来正解应该怎么做。首先对于上面的ci,可以把它看成一个以mi为根的多项式:
而在模p下天然有一个以mi为根的多项式:
所以如果求解两者的gcd就会得到:
就有mi了。
但是,f、g的次数太大仍然是个问题,对于这一点的处理和我在NSSCTF的dlc出的一道Franklin有点类似。由于f的次数较低,所以可以用f做商环,将g一步一步lift上去,之后再用HGCD求出两者的公因式,而在商环上lift的过程sage内部是有实现的。
然而,2^24这个数量级好像刚好超过了sage能处理的次数上限,所以没法直接做,并且由于有多个分组都要这么处理,所以可能要自己用c++手动写个多项式的lift,并且用更大内存的机器来跑才行。
要我写这个的话,我短时间是肯定憋不出来的,但是如果赛中早点想到这个思路,然后交给@leukocyte感觉肯定能写,还是有点可惜,自己出过的类似题没有联想上。
Forghan(36 solves , 119 pts)
题目描述:
1 | The Forghan, the combination of RSA and DLP cryptography, may in certain instances prove more accessible than employing either method individually. |
题目:
1 | #!/usr/bin/env sage |
题目有三个选项,但是显然是有顺序的,具体来说应该按照下面来:
- 选择”S”,可以输入256bit的素数p、q
- 选择”G”,靶机对flag进行加密,加密流程如下:
- 生成n,$n = (p^2-1)(q^2-1)$
- 分别生成p、q下的一个随机二次非剩余gp、gq
- 生成p、q下的随机数sp、sq
- 将flag分为两段,记为flagp、flagq,对应数字记为mp、mq
- 计算yp、yq,$y_p = g_p^{s_p}\quad(mod\;p) , y_q = g_q^{s_q}\quad(mod\;q)$
- 计算密文cp、cq,$c_p = m_p^{y_p}\quad(mod\;n) , c_q = m_q^{y_q}\quad(mod\;n)$
选择”P”,可以拿到gp、gq、yp、yq的值
由于有yp、yq,所以对于密文最后一步的计算来说,其实就相当于解一个RSA,只是模数n变成了:
由于flag是静态的,所以完全可以放在一个子群里去求解,比如放在模p-1下:
也就是说,只要知道p-1的分解,就可以求phi(p-1),然后就可以解RSA解出mp、mq在p-1下的值,又由于flag是静态的,所以交互多次求crt,就能得到flag的完整值。而p、q都是自己构造的,所以想满足p-1能分解太容易了,比如最简单的情况就构造:
令k是一个素数,就有:
之后的求解就很容易。
exp:
1 | from Crypto.Util.number import * |
如果这题需要用到DLP的话,那构造p-1光滑应该是好点,然而sp、sq完全用不到,所以不用考虑。
Honey(48 solves , 95 pts)
题目描述:
1 | Honey is a concealed cryptographic algorithm designed to provide secure encryption for sensitive messages. |
题目:
1 | #!/usr/bin/env python3 |
params_enc.txt:
1 | p = 10580731215444436219213907263947534038012197972307836319229421193761088798378768844649759133142120180834573817149711299466707823017636232456526471274387917 |
题目给了d组如下等式:
所有c、Q、R、S均已知,要求还原m。同时,每次的ri、si都是d bit的数,p是512bit。
由列表长度可以知道d就是32,所以r、s都是很小的量,因此自然想到消去m做一个HNP。消去的方式也很朴素,就是取第0组和第i组的等式:
分别将m前系数乘至相等:
然后作差就消掉m了,之后就是造个格子去做HNP就行。
exp:
1 | from Crypto.Util.number import * |
可以看到m其实也不大,所以不消m直接规约也可以。
Joe-19(120 solves , 47 pts)
题目描述:
1 | Joe-19 is a cryptographic system that leverages a top-secret version of GPT AI technology to develop advanced and robust cryptographic tools. |
题目:
1 | #!/usr/bin/env sage |
output.txt:
1 | n = 8098851734937207931222242323719278262039311278408396153102939840336549151541408692581651429325092535316359074019383926520363453725271849258924996783681725111665666420297112252565291898169877088446887149672943461236879128453847442584868198963005276340812322871768679441501282681171263391133217373094824601748838255306528243603493400515452224778867670063040337191204276832576625227337670689681430055765023322478267339944312535862682499007423158988134472889946113994555274385595499503495488202251032898470224056637967019786473820952632846823442509236976892995505554046850101313269847925347047514591030406052185186963433 |
看这题的时候一脸懵逼,这意思是不是用65537去连续拼接得到一个512bit的素数p?尝试了一下无果之后就先跑去做别的题目了。
之后回来看发现已经被@Astrageldon解决了,不过文档里没有写过程。之后又问了下@Zima,他告诉我可以:
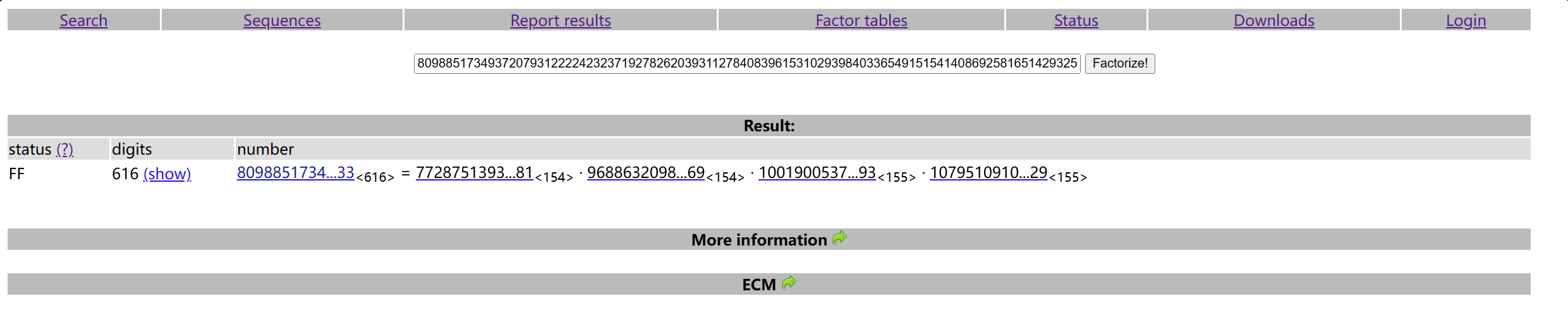
XD
exp:
1 | from Crypto.Util.number import * |
之后看春哥的wp才知道题面的e说的是自然对数那个e,所以预期应该是要枚举这个数字的连续bit去找素数。
Melek(66 solves , 73 pts)
题目描述:
1 | Melek is a secret sharing scheme that may be relatively straightforward to break - what are your thoughts on the best way to approach it? |
题目:
1 | #!/usr/bin/env sage |
output太长就不放在这,可以去NSSCTF下载附件。
这个题目过于直白,首先在模p下建立一个度为t-1的多项式f,其中常数项是flag加密后的密文,其他系数均未知。然后随机给出了t个点值对,并且给了e、p的值。显然拉格朗日插值过后再对e求一次关于p-1的逆就行。
exp:
1 | from Crypto.Util.number import * |
Nabat(25 solves , 159 pts)
题目描述:
1 | Nabat is a cryptographic challenge that explores the representation of polynomials within a specific polynomial ring structure. |
题目:
1 | #!/usr/bin/env sage |
题目有12轮挑战,每轮挑战会先生成一个随机数n(随着轮数变大),需要给出一个多项式f,f满足四个条件就可以通过本轮挑战:
- 所有系数需要为1,0,-1
- f的度d要大于等于$2logn - 1$
- 系数为0的数量要大于等于$\lfloor \frac{2d}{3} \rfloor-3$
- f-n是g的因子
其中,g是:
和其他商环类题一样的思路,由于在模g下有:
所以:
同理就有:
所以说其实整个多项式f的系数的产生过程,其实可以看作是从常数n开始的向高次项系数的迭代。而为了满足剩下三个要求,通俗一点来说就是要迭代的越彻底越好,也就是每一项的系数都要尽可能消成0。
那就从常数n开始思考,假设他约减了k0个2之后变成1、0或者-1,记这个系数为a0,也就是:
那么接下来,一次项和二次项的系数就变成了k0,对于一次项来说,其约减k1个2之后变成a1,a1同样只能取1、0或者-1,那么这个k1又会贡献给二次项和三次项,所以二次项会从k0+k1开始约减,依此类推。整个多项式系数就会变成如下的线性迭代过程:
所以对上面的格进行规约就可以得到需要的结果。至于度怎么选择,为了满足题目条件的话应该是越大越好?这里我取了400。
exp:
1 | from random import randint |
这个题目赛中的时候,在未更新之前,其实一共需要通过40轮,并且条件3限制为:
- 系数为0的数量要大于等于$\lfloor \frac{2d}{3} \rfloor$
可以用这个方法检查一下,发现通过概率低了很多很多。赛中@leukocyte和@hash-hash也是利用三值多项式来约减系数,不过应该是用了另一个策略来满足后三个条件。然后大家一起挂那个脚本,最好的时候也就挂到了28轮。看discord才发现果然又是题的问题。
Nazdone(35 solves , 122 pts)
题目描述:
1 | Nazdone is a cryptographic exercise focused on the practical challenges of generating random prime numbers for real-world applications. |
题目:
1 | #!/usr/bin/env python3 |
output.txt:
1 | n = 301929748923678449872944933611657670834216889867340028357609265175830693931365828840717548752313862343315133541384709574659039910206634528428504034051556622114290811586746168354731258756502196637977942743110508997919976400864419640496894428180120687863921269087080600917900477624095004141559042793509244689248253036809126205146653922738685595903222471152317095497914809983689734189245440774658145462867680027337 |
题目的params由三个未知量m、a、z构成,利用这三个值生成了三个素数p、q、r,具体生成过程也就是sol函数,流程是:
取p初始值,为1或者2
随机打乱1到a的列表,并取前z项,记为a1,a2,…,az,之后将p加上如下值:
其中bi是随机的0或者1
检查p是否是素数,是的话就返回
可以看出,其实p就等于:
或者:
而p、q、r都是这种类型的素数,其乘积构成n。最后按如下方式加密:
仅给出n、c,要求还原flag。
首先,对于params的三个参数m、a、z可以说是一无所知,必须要利用n来还原他们,还原的依据就是p、q、r满足的等式。不妨假设他们都是第一种类型(第二种同理),那么n就该等于:
可以看出,如果进行展开的话,在模m下n就为1(如果是第二种类型就为8),因此我们可以简单爆破一下,就可以拿到m:
1 | from Crypto.Util.number import * |
但是这样可以发现备选项还是有一点多,这个时候就要利用另一个事实,也就是bi只会是0或1这个条件。仍然用第一种情形进行讨论,n减去1后,他应该是一个较稀疏的m进制数才对(第二种类型则为n-8)。所以可以优化一下刚才的脚本来得到更符合要求的m:
1 | from Crypto.Util.number import * |
输出的数据是:
1 | 2 706 |
可以看出m很可能等于19。
然后用.log检查一下n在19进制下的最大次数,可以发现是321,说明p、q、r三个素数的次数差不多都在107左右。而又因为作为m进制的数字,其系数都为0或1,因此就只需要做个深搜即可,深搜思路和二进制下深搜基本没差:
1 | def find(pl,ql,rl,h): |
得到p、q、r:
1 | p = 3530869780887683268140728773245395170410635845517928489976021534009516369358447511411853596093628646212566313257712207746790503704123439 |
然后就是常规RSA解密,虽然z并不知道,但是显然范围也很小,所以爆破就好。
完整exp:
1 | from Crypto.Util.number import * |
RM2(64 solves , 75 pts)
题目描述:
1 | The RM2 cryptosystem is a minimalist design that exhibits remarkable resilience, making it exceptionally difficult to compromise. |
题目:
1 | #!/usr/bin/env python3 |
简单来说,题目可以输入两个1024bit的素数p、q,之后会生成一个随机字符串s,将其分为两部分后分别变为整数m1、m2,并计算:
给出c1、c2,如果之后能正确输入s,就可以拿到flag。
两个都可以看做是RSA,所以只要知道模数的全部分解就可以做了。而对于两者来说都可以用一个很简单的方法去构造:
- 生成素数k
- 令p=2k+1
- 检查p和2p+1是否都是素数
如此一来就有:
然后就解RSA就行了。
Soufia(36 solves , 119 pts)
题目描述:
1 | The Soufia equation incorporates an undisclosed random oracle function. Can you analyze the equation and infer the unknown function's value? |
还是没有附件,和Bada类似,题目内容是:
存在一个未知的函数f,满足:
给出两个点值对:
要求可以对任意的f(x)求出x。
这种函数方程题目一般来说要做以下几个事情:
- 去掉多层复合
- 代一些特值
比如对于这个题目的函数f,先令x=0有
然后令y=0,x=y就得到:
作差就可以去掉双层复合,得到:
其实到这里可以看出一点端倪,就是:
这其实也可以看作是:
上式对于任意的y恒成立,也就有:
是一个常函数。而显然当f(x)是线性函数一定满足这个条件,所以直接由题目两点建一个线性的f(x)就可以了。
而说到这个题目就不得不吐槽一下他的靶机,这个靶机从开始到比赛结束,整个队伍里都只有@上辰能连上,发邮件给主办方,他们也没增加这个题目的靶机。@hash-hash在做这个题的时候怎么连怎么挂,非常折磨。
Vantuk(51 solves , 90 pts)
题目描述:
1 | The Vantuk equation is complex, designed to conceal flag components, yet it appears deceptively simple on the surface. |
题目:
1 | #!/usr/bin/env sage |
output.txt:
1 | A = 6080057478320734754578252336954411086329731226445881868123716230995225973869803901199434606333357820515656618869146654158788168766842914410452961599054518002813068771365518772891986864276289860125347726759503163130747954047189098354503529975642910040243893426023284760560550058749486622149336255123273699589/10166660077500992696786674322778747305573988490459101951030888617339232488971703619809763229396514541455656973227690713112602531083990085142454453827397614 |
题目将flag分为两段m1、m2,并取一个随机数a,之后给出以下几个值:
要求还原flag。
由于A仅仅是关于a的式子,所以利用其分子分母两个方程应该可以解出a来,注意到分子分母可能有经过化简,所以把化简的倍数k也当作变量,去解一个二元方程组:
1 | t1 = 6080057478320734754578252336954411086329731226445881868123716230995225973869803901199434606333357820515656618869146654158788168766842914410452961599054518002813068771365518772891986864276289860125347726759503163130747954047189098354503529975642910040243893426023284760560550058749486622149336255123273699589 |
解得a为:
1 | 598038828088293688046274960163455723857293440615241291237111095137601911115982565871162542905677325967979821954570041947800148887293534420144379636905742 |
得到a之后的步骤就同理了,只不过变成利用U、V去解关于m1、m2、k1、k2的方程而已。
exp:
1 | from Crypto.Util.number import * |
Hard
Chochol(15 solves , 226 pts)
题目描述:
1 | Chochol is an unusual cryptosystem that encrypts messages by blending them within elliptic curves - see if you can crack it. |
题目:
1 | #!/usr/bin/env sage |
output.txt:
1 | Gp = (2024, 77522466419731346352388161327659294096) |
题目非常非常的直白,给出两条椭圆曲线:
然后生成随机数s,并给出四个点Gp,Gq,Hp,Hq,满足:
最后把flag进行RSA加密并给出c:
要求还原flag。
要解最后的RSA,不仅要有加密指数s,也需要有n的分解,而我们的数据仅有密文c和四个点Gp,Gq,Hp,Hq,并没有他们所在有限域的信息。所以第一步只能是利用点在曲线上这个信息,去消a或者做一次groebner得到一个p的倍数k1p,同理也就有k2q。由于p、q都只有128bit,所以挂yafu有机会分解出来,又因为两个曲线a相同,所以两个一起挂,谁更快挂出来就可以直接求a,那另一个就可以不用挂了。
得到p、q之后就好办了,对同源熟悉一些的话可以知道p、q模4余3并且是这个曲线方程形式时,这是一条超奇异椭圆曲线,阶为p+1,所以既可以做MOV attack求出s,也可以选取p+1的一些小因子和q+1的一些小因子去Pohlig-Hellman,再crt起来就行。
exp:
1 | from Crypto.Util.number import * |
这个题开始flag值不对,和@yolbby一起做出来之后怎么都交不上。这全是可见字符,语句还有意义,这还能不对?发邮件给主办方之后发现确实是他们设置错了。。。
Imen(19 solves , 194 pts)
题目描述:
1 | Imen presents a challenging task involving a novel and creative cryptosystem, inviting you to attempt to break it and obtain the flag. |
题目:
1 | #!/usr/bin/env sage |
题目共12轮挑战,每一轮挑战流程是:
生成素数p,大小随轮数增加
生成 $l$ 个模p下的矩阵,个数也随轮数增加:
随机打乱矩阵次序后,计算乘积M:
给出M和按顺序的矩阵列表,要求计算出这个置换
完成全部12轮挑战就可以拿到flag了。
注意到生成矩阵Ai时,除了固定的维数k、随机的素数p以外,还有一个参数是B,他把A中的每个元素限制在了0-B内。生成几组数据可以发现,这样做之后,M其实根本就没有模p,是在ZZ上成立的。
所以思路就很好办,我们枚举A中的所有元素As,去计算:
逆矩阵在ZZ下求即可,可以发现,由于矩阵乘法没有交换律,所以当且仅当枚举到As为Ai的时候,恰好可以消掉,也就是:
所以仍是一个ZZ下的矩阵,而其他的矩阵会导致T不再是ZZ下的矩阵,因此就可以求出置换了。(因为ZZ并不是一个域,里面除去0的元素并不都有乘法逆元,所以求逆会出现分数)
可以用下面的脚本简单验证这个思路的正确性:
1 | from Crypto.Util.number import * |
这个题目在没有update之前,好像最后几轮矩阵的值会超过p,可能就不太好做了。还有这个题目的输入输出处理更是依托。
Latifa(22 solves , 174 pts)
题目描述:
1 | Latifa is a tricky yet enjoyable challenge, akin to solving a puzzle in a dream-like state. |
题目:
1 | #!/usr/bin/env sage |
output.txt:
1 | c = 1.802740943639362458394687428102524270510281665315000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000e47 |
6.9的凌晨六点左右,我和@yolbby做完Chochol之后怎么都交不上flag(原因就是上面说的,主办方flag设置错了)。然后他说他去看点别的,就去看了这个Latifa。
结果10分钟左右他就做完回来了:
然后就好奇地来看了一下这个题目,他用未知的b、g,对flag进行了如下加密:
把上下的g约一下得到:
由于这学期刚好选修了一门电子信息数学基础,重温了下高数,所以看到这个想到了定积分,但是既然十分钟就能搞定,应该不是这么做的吧?
首先可以发现c最后的值一定包含因子b,所以先查一下c的所有因子组合找一下b。但是根本不知道怎么判断b正不正确,所以打印了一下long_to_bytes,结果就出了……
我也很懵,看了下yolbby写在文档的东西也是这么做的,等他期末考完问问他当时做这个是怎么想。
exp:
1 | from Crypto.Util.number import * |
O7R(23 solves , 169 pts)
题目描述:
1 | The O7R cryptosystem combines RSA key recovery techniques with a 7-segment digit representation, resulting in a unique and robust design. |
题目给的是pdf文件,核心一点的部分是:


数据:



先阐述下题目内容,题目给出了用七段数码管表示的p、q、n、n^2、c等五个数值,他们满足:
- c是没有损坏的(也就是c的所有数字都完好)
- 剩余的四个数值,都是经过了损坏的,损坏的含义是:每个七段数码管表示的数字,有50%的概率爆掉随机一根数码管
要求还原flag。
首先明确这个损坏的含义,50%的概率爆掉随机一根数码管,也就是说一个数字可能根本不会坏,就算损坏了,也最多是一根数码管不亮。所以对于其中每一个数字,他的可能性都是有限的,比如举几个例子:
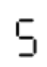
这个可能是5、6或9。
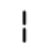
这个可能是1、7。
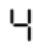
这个只能是4,因为最多掉一根管,他补任何一个地方都不会成为其他数字。
这么看来的话,只需要把每个数字的可能性都列出来,然后深搜剪枝就可以了。由于每个数字的可能性都不多(最多也就是上面这个5的情况,共3种),所以其实完全不需要n^2,直接用pq=n来剪枝就行。
思路很清晰,但是怎么样做才能方便地把每个数字的可能性都列出来?和@yolbby合计了一下,与其切分图片提像素然后分类,不如直接肉眼一个一个写,我写p、他写q,然后再分行写n。为了统一,把可能性写成二重列表的形式如下(用p的前几位举例):
1 | [[7],[3],[2],[6,8],...] |
折磨就这么开始了,凌晨的时候,两个人盯着电脑屏幕老眼昏花的写,而且每个位置还要仔细地去想所有的可能性,因为漏了就很麻烦。
然后又拉着@Zima一起折磨,好不容易把p、q、n全部写完了,一剪发现连10位都剪不出来,说明最后十位就有错。然后三个人又一起debug。debug老半天终于把p、q剪出来了,然后发现好像还没有弄c,不过c挺好办,因为没有损坏,但是直接OCR识别出来的还是不少错(特别容易漏1),然后又是一起肉眼debug才把c弄出来。
exp:
1 | from Crypto.Util.number import * |
痛苦。TT
Solmaz(11 solves , 271 pts)
题目描述:
1 | Solmaz has developed a simple and visually appealing cryptosystem based on Elliptic Curve Cryptography, but its potential vulnerabilities require further investigation. |
题目:
1 | #!/usr/bin/env sage |
output.txt:
1 | P = (1338, 9218578132576071095213927906233283616907115389852794510465118810355739314264) |
题目生成4个32bit的素数,记为q1、q2、q3、q4,然后计算:
然后取随机数c,得到模p下的椭圆曲线,满足阶为p-1:
由于p模4余1,所以这个构造和前面的Chochol又不一样,虽然形式相同,但并不是超奇异的,所以才能使阶为p-1
之后给出曲线上的两个点P、Q,满足Q=mP,要求还原m。
依然没有模数p和c,所以同样做groebner得到一个p的倍数kp,然后由于p-1显然是个光滑数,所以想到利用Pollard p-1来分解他。
但是虽然说确实光滑,但是32bit的素数好像还是稍微大了一些,但是之前在maple博客有一篇文章看到过一个叫gmp-ecm的工具好像可以用:
N1CTF 2022 Writeups | 廢文集中區 (maple3142.net)
然后就在队伍里问了问有没有师傅用过,@Zima和@leukocyte试了一下好像不太行,可能是因为每个素因子都平方了一下的缘故。
所以最后还是想着直接写一个p-1光滑的分解脚本,回顾一下Pollard p-1的原理,其实就是构造一个t,使得:
那么由于费马小定理,就有:
所以可以求:
从而得到p。
关键的一步就是怎么构造出这样的t,由于:
所以只要从4开始,乘上所有32bit素因子的平方,这样的t就一定是p-1的倍数。
而要遍历所有32bit的因子,对于python而言有点大了,所以想的是用C++的NTL库去做这个事情。但配这个环境好像实在有点麻烦,所以交给了Zima。Zima提示说gmpy2的nextprime也许可以,所以我也就写了个python的脚本挂着,结果挂了一小时左右真的出了分解。
分解完就好做了,由于保证了阶为p-1,p-1也光滑,所以直接求DLP就可以。
exp:
1 | from Crypto.Util.number import * |
这个题也很扯,开始的附件里求完m发现不对,等了一会儿发现果然又要redownload。
Tesvir(27 solves , 150 pts)
题目描述:
1 | Tesvir, an advanced and unbreakable cryptosystem, emerged as a revolutionary development in the 20th century cryptographic landscape. |
题目:
1 | #!/usr/bin/env sage |
输出也有点长,不放在这里了。
先梳理一下题目内容。首先是gen_params:
- 生成有限域:
- 生成一个1-223的随机置换r
- 生成度为24的不可约多项式f
- 生成F的生成元g
- 把f转到F下并求出根t
然后是genkey:
生成一个随机数d
再生成一个1-223的随机置换pi
对0-223的j,分别计算bj,满足:
计算cj,满足:
所有cj作为公钥
说实话,看到这里真的一头雾水,gen_params的内容以及这个223让我联想到之前学了一点点的Reed Solomon Code,但是本身就学了点皮毛,完全不会用。然后这个genkey也一点没看出要干嘛。
总之先继续往下,还剩一个encode和encrypt,具体来说encode是:
- 把明文按24bit分成若干组,分别进行加密
- 对于每个分组m,填充0使其长度为223
- 之后,从末尾开始将0换成1,使得最终的m一共含有24个1
最后是encrypt:
- 对于每个m,计算向量m和C在模p^h-1下的内积
看完发现这不就是个背包吗,而且由于每个m其实都只由24bit生成,一一对应,所以直接爆破就好了,也就是对所有24bit的m,计算最后的密文值来建立字典,然后查字典就行。
又因为m只能是可见字符,所以只需要用可见字符建字典就够了。
exp:
1 | from Crypto.Util.number import * |
不过flag头为什么不是CCTF?
Tough
Capac(5 solves , 375 pts)
题目描述:
1 | Capac is a specialized case of elliptic curve cryptography, which we've used to develop a new system. Fully cracking it requires deep understanding of all details. |
题目:
1 | #!/usr/bin/env sage |
output.txt:
1 | pubkey = (88952423353141033373010851411899063207359252317845617788486152084097996161951607075526045796294269180195617694600310298365306053247057038631088894596240751441036842918276089201617169287026865078594774765749720881882802881828282593949861999972983150274426090825607252511101783484830324425960589823065107734367701062429129988752511807642589018556438468736528286490143324590323667921809, 14614034441012778293137473086633630265649701969941154268770044720080815753509578891278180391973505358690528554774945713350178015180660958849492699471696540533037229348328187546698408636098560882156797223120456953146198082440467610904542891004365972384778900094467795995848069039170326511960815050814119987884996078973626805712610037071776396313451847840676985037388757858071864447123) |
最重量级的一题。
题目基于Cubic Pell Curve的加密,和前段时间DASCTF的一样,关于这个加密系统的论文是:
具体加密和解密步骤参考论文就可以了,总之只要有私钥——也就是n的分解的话就可以做。其中n是这样的形式:
其中p、q均为128bit的素数。
问题就在于,整个题目就完完全全是把这个加密实现了一遍,完全没看出什么漏洞,那怎么解?不过考虑到p、q都是128bit,说大的话也不算大(前面几个题不也是128bit挂yafu吗),所以还是先给n开了个根之后挂了个yafu。一时半会儿没有动静,就先挂住了。
距离比赛结束还剩几小时的时候,实在觉得又困又饿(通宵+没吃饭),其他题也做的差不多了,就想着差不多出门吃个饭,这个时候想起还挂了个yafu,然后切过去看了看:
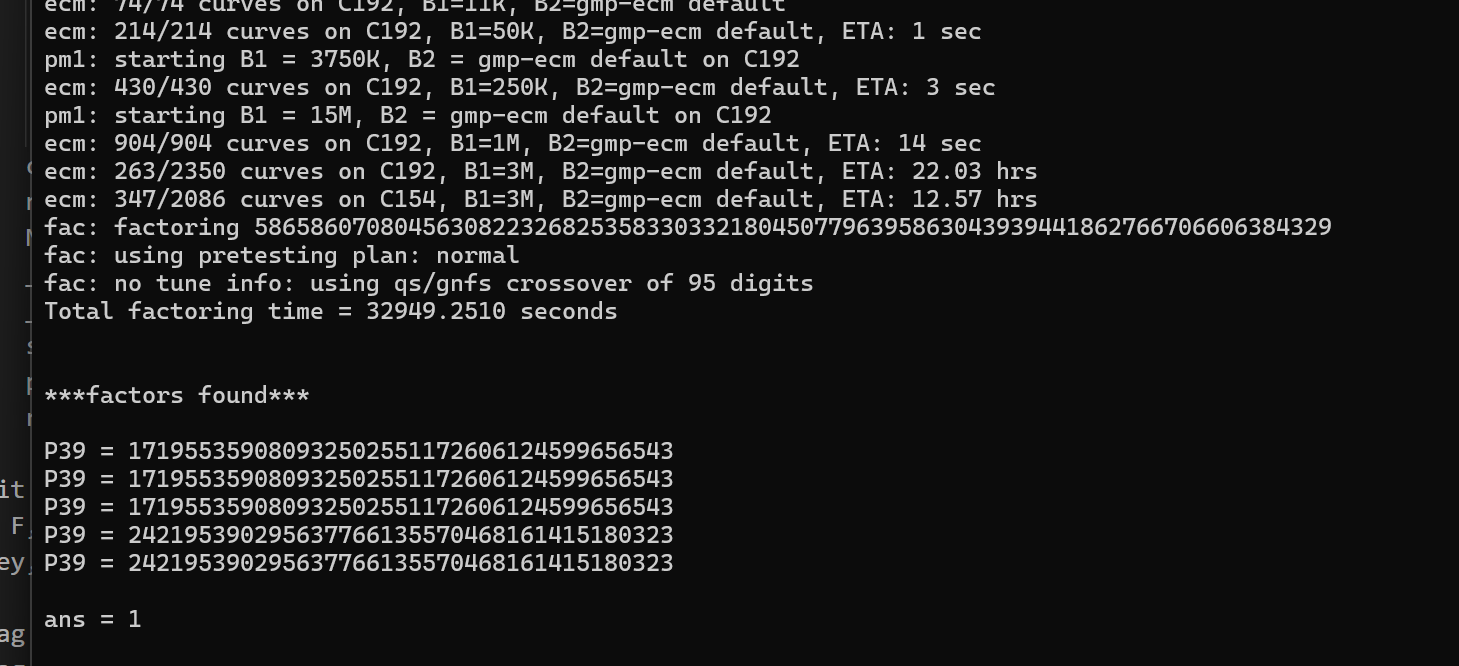
太逆天了,硬挂32949.2510秒出了分解,所以说factorCTF不是没有道理,发到群里大火也炸锅了哈哈哈:
之后把这个分解给@hash-hash(因为他之前解过DASCTF那个,应该改一改就能用),也是很快就搞定了,这里偷懒搬一搬他的脚本:
1 | from Crypto.Util.number import * |
这个题就这么结束了,有点奇妙。
赛后看deebato他们硬挂yafu没直接显示结果,但是在log里找到了分解,突然感觉我这里分解出因子的时候可能也远远不到32949.2510这么多秒,只是程序没运行完没显示罢了,又学到一招。
关于这个题,其实赛中@yolbby想出了一个很合理的思路,只是对于这个题的数据来说并不太适用,我把他的想法出成了一题,放在了NSSCTF上
相对于这个题目,仅仅是把p、q改成了512bit,别的都没有变,有兴趣的师傅可以做做看
Jonon(13 solves , 247 pts)
题目描述:
1 | The Jonon challenge is a variation of the Imen challenge, and it provides a similar level of difficulty as the original version - it's an enjoyable experience. |
题目:
1 | #!/usr/bin/env sage |
output比较长,也不放在这里。
可以看出这个题和Imen相当的神似,只是稍稍变了一些。先把genkey梳理一下:
生成l+1个模p下的矩阵:
生成随机数s
将sA打乱后,计算其乘积pE:
计算:
再依次计算下面矩阵的值得到列表,并和sA(不包含sD)和pE一同作为公钥pkey:
打乱后的列表L,s,sE和sD作为私钥
然后是encrypt:
先生成一个1-l的随机置换pi,并用这个置换生成flag(也就是求出置换就有flag)
生成pkey,skey
计算C:
要求求出置换。
首先,所有矩阵都是模p下的,虽然我们并没有p,但是我们有所有的:
求逆得到:
所以有:
然后又因为逆矩阵具有下面的性质:
所以说上面的式子又可以变成:
也就是:
而这几个矩阵都是公钥里的,所以可以在ZZ上直接求这个矩阵,那么两者的行列式在模p下应该相等,所以可以多求几组作差,然后gcd就得到p了。
有了p过后,又因为:
所以又很轻松就可以在模p下计算出sD来。
之后就很好办了,现在我们拥有C,要求对应的置换:
而可以看出,首位的sE和sE^(-1)无非是对矩阵做了相似,而相似前后,矩阵的迹是不会变的,又因为sA和sD都较小,所以可以通过枚举sA,然后判断迹是增大还是减小来检查枚举的是否正确,就得到了置换。
然而有个细节需要注意,那就是题目设置的数量级会使得最终C的迹也会超过p的大小,所以先枚举出可能的初始路径之后,再进行搜索才行。
exp:
1 | from Crypto.Util.number import * |
和Imen一样,这个题的输出也是依托,要自己处理一下变成列表形式。
Rehawk(9 solves , 300 pts)
题目描述:
1 | Rehawk is an advanced, modern cryptosystem of great complexity that only seasoned cryptographers can comprehend, with few able to successfully break it. |
题目:
1 | #!/usr/bin/env sage |
output.txt:
1 | [ -4602774218265912404*zeta1280^31 - 25509381853469544908*zeta1280^30 + 129376017982404349488*zeta1280^29 + 716286531689185935744*zeta1280^28 - 1632208466401721293158*zeta1280^27 - 9028003170806549615013*zeta1280^26 + 12206704950441875625482*zeta1280^25 + 67457290883578785545644*zeta1280^24 - 60204416625997809670344*zeta1280^23 - 332433796634335506443469*zeta1280^22 + 206123873952616279215906*zeta1280^21 + 1137323310449735580891532*zeta1280^20 - 502186108465894748616016*zeta1280^19 - 2769056905000016534751538*zeta1280^18 + 878039249325641175319414*zeta1280^17 + 4838663751293786838127040*zeta1280^16 - 1097188014524649363149070*zeta1280^15 - 6043236501081735721161712*zeta1280^14 + 964124818127455367449150*zeta1280^13 + 5308004439355857834330485*zeta1280^12 - 578006232877698984851372*zeta1280^11 - 3181061779748249841736219*zeta1280^10 + 224962785316232564841220*zeta1280^9 + 1237722919632690072191185*zeta1280^8 - 52424883340535911897910*zeta1280^7 - 288372879182213647372365*zeta1280^6 + 6357946814410664097444*zeta1280^5 + 34967804349427160519879*zeta1280^4 - 302245973040480152708*zeta1280^3 - 1662172616495876145310*zeta1280^2 + 2366049046813041208*zeta1280 + 13011646416303986233 20341475869141650336*zeta1280^31 + 1951592807564566629*zeta1280^30 - 571077856249690441621*zeta1280^29 - 55295108849716726354*zeta1280^28 + 7196660823549758544764*zeta1280^27 + 702767505392614093619*zeta1280^26 - 53765538109270297626741*zeta1280^25 - 5291465118503133518883*zeta1280^24 + 264923914169814211875106*zeta1280^23 + 26259460116858500856269*zeta1280^22 - 906245929396843087071465*zeta1280^21 - 90407733487003834471466*zeta1280^20 + 2206203021593936629146834*zeta1280^19 + 221362527660366178501972*zeta1280^18 - 3854747120193508447272846*zeta1280^17 - 388741550159692397343437*zeta1280^16 + 4813958180021168270877045*zeta1280^15 + 487624064628609110025176*zeta1280^14 - 4227967989714953615984050*zeta1280^13 - 429881071729752134763778*zeta1280^12 + 2533644029049790041455129*zeta1280^11 + 258414888967057871397446*zeta1280^10 - 985769426015678192342018*zeta1280^9 - 100792924475518106238832*zeta1280^8 + 229662454242100806590311*zeta1280^7 + 23526719373273264108474*zeta1280^6 - 27847921707112376241503*zeta1280^5 - 2856416535680139555816*zeta1280^4 + 1323714816988549264238*zeta1280^3 + 135871497938828491146*zeta1280^2 - 10362137493026264546*zeta1280 - 1063759814089207676] |
这个题目看了一眼我就被劝退了,又是分圆域又是hermite矩阵的,看着就头大。
然后@yolbby一语点醒梦中人,定位到这里:
1 | skey = Matrix([[a, _c], [b, _d]]) |
可以看出skey和pkey都是2x2的矩阵,并且还存在关系如下:
而其实这相当于四个方程四个未知数,只是元素在一个陌生一点的域中而已,sage依然是可以正常处理的。也就是说,用这四个方程去resultant就可以把skey完全解出来。又由于flag是根据skey生成的,所以解出来之后就可以拿到flag。
exp(from yolbby):
1 | from hashlib import sha256 |
Vorop(7 solves , 334 pts)
题目描述:
1 | Vorop is a post-modern cryptosystem with diverse applications in finite fields and matrices - thoroughly analyze it to attempt breaking it. |
题目:
1 | #!/usr/bin/env sage |
知识盲区,按@hash-hash的说法是基于多变量的一道题目,之前稍微看过一点多变量,但除了还记得油变量和醋变量之外,其他的完全不懂了。
直接写attack好像很折磨,hashhash就发动群友一起找现成的attack,然后@leukocyte找到了这篇:
https://eprint.iacr.org/2024/279.pdf
里面有实现:
https://github.com/River-Moreira-Ferreira/prov-attack
hashhash稍微调调就能用了,但我确实是一点都整不明白,直接躺好。而且hashhash好像还发现了个非预期。
然而奇怪的事情又发生了——交互总是会卡在第33轮,开始怀疑是网的问题,所以大家都跑了一遍,都卡在33轮。leukocyte最后发现他远端下发的参数和题目附件的不一样,对应改一改就好了。
但还是完全不懂多变量,有空学一学。
总结
虽然比赛槽点很多,但是总而言之,一群喜欢密码的师傅聚一块儿打比赛本来就是很开心的事情,明年继续加油。
还有就是比赛结束第二天去CTFtime建战队的时候发现cyberCryer这个战队名被 抢 注 了,真是离了大谱。给CTFtime发feedback过后恢复了正常,然而排名似乎不太好改了,发feedback、发邮件甚至去推上at都没有人理,伤心。