2023-NewStarCTF-wp-crypto

比赛记录

Week 1

题目很基础，这里就不讲了。

Week 2

挑一道题说一说。

partial decrypt

题目描述：

解密, 但是只解密一半

题目：

from secret import flag
from Crypto.Util.number import *

m = bytes_to_long(flag)
e = 65537
p = getPrime(512)
q = getPrime(512)

n = p*q 

c = pow(m,e,n)

dp = inverse(e, (p-1))
dq = inverse(e, (q-1))
m1 = pow(c,dp, p)
m2 = pow(c,dq, q)
q_inv = inverse(q, p)
h = (q_inv*(m1-m2)) % p
print('m2 =', m2)
print('h =', h)
print('q =', q)

# m2 = 4816725107096625408335954912986735584642230604517017890897348901815741632668751378729851753037917164989698483856004115922538576470127778342121497852554884
# h = 4180720137090447835816240697100630525624574275
# q = 7325294399829061614283539157853382831627804571792179477843187097003503398904074108324900986946175657737035770512213530293277111992799331251231223710406931

之所以想说一下这个题，是因为可能不少cryptoer随便试了试，发现h*q+m2就能得出答案，却不明白这是否是一个巧合。

这里先说结论，无论明文m长度多大，只要他小于n，这个求解方法都是完全可行的，原理如下。

首先由题目可以看出，m1，m2其实就是：

$$m1 \equiv m \quad(mod\;p)$$ $$m2 \equiv m \quad(mod\;q)$$

我们先把此处的模等式展开，写成等式形式：

$$m1 = m - k1*p$$ $$m2 = m - k2*q$$

然后，由题目知道，h满足：

$$h \equiv q^{-1}(m1-m2) \quad (mod\;p)$$

不妨把刚才得到的等式代入上式：

$$h \equiv q^{-1}(m - k1*p-(m - k2*q)) \quad (mod\;p)$$

即：

$$h \equiv q^{-1}(k1*p + k2*q) \quad (mod\;p)$$

展开就能消去q^-1*q，得到：

$$h \equiv q^{-1}*k1*p + k2 \quad (mod\;p)$$

又因为在模p意义下，所以：

$$h \equiv k2 \quad (mod\;p)$$

而这两者仅仅是模p下相等吗？事实上他们完全相等，这是因为：(//代表整除)

$$k2 = m // q < n // q = p$$

也就是说k2<p，因此k2模p等于没模，所以k2 = h。

因此就有：

$$m2 + h*q = m2+k*q = m$$

所以上式一定成立，因此就能恢复明文。

exp：

from Crypto.Util.number import *

m2 = 4816725107096625408335954912986735584642230604517017890897348901815741632668751378729851753037917164989698483856004115922538576470127778342121497852554884
h = 4180720137090447835816240697100630525624574275
q = 7325294399829061614283539157853382831627804571792179477843187097003503398904074108324900986946175657737035770512213530293277111992799331251231223710406931
e = 65537

m1 = h*q + m2
print(long_to_bytes(m1))

#flag{rsa_with_crt#b12a3a020c9cc5f1a6df4618256f7c88c83fdd95aab1a2b2656d760475bd0bf1}

Week 3

Rabin’s RSA

题目描述：

Michael O. Rabin的加密方案

题目：

from Crypto.Util.number import *
from secret import flag
p = getPrime(64)
q = getPrime(64)
assert p % 4 == 3
assert q % 4 == 3

n = p * q

e = 2
m = bytes_to_long(flag)

c = pow(m,e,n)

print('n =', n)
print('c =', c)

# n = 201354090531918389422241515534761536573
# c = 20442989381348880630046435751193745753

首先观察到n较小，因此可以直接factordb分解出p、q。然后就是普通Rabin加密，原理不详述了。

exp：

from Crypto.Util.number import *
import gmpy2
import math

n = 201354090531918389422241515534761536573
c1 = 20442989381348880630046435751193745753
e = 2
p = 13934102561950901579
q = 14450452739004884887

def  merge(a1,n1,a2,n2):
    d = math.gcd(n1,n2)
    c = a2-a1
    if c%d!=0:
        return 0
    c = (c%n2+n2)%n2
    c = c//d
    n1 = n1//d
    n2 = n2//d
    c *= gmpy2.invert(n1,n2)
    c %= n2
    c *= n1*d
    c += a1
    global n3
    global a3
    n3 = n1*n2*d
    a3 = (c%n3+n3)%n3
    return 1
def exCRT(a,n):
    a1=a[0]
    n1=n[0]
    le= len(a)
    for i in range(1,le):
        a2 = a[i]
        n2=n[i]
        if not merge(a1,n1,a2,n2):
            return -1
        a1 = a3
        n1 = n3
    global mod
    mod=n1
    return (a1%n1+n1)%n1
def exCRT_getequation(a,n):
    a1=a[0]
    n1=n[0]
    le= len(a)
    for i in range(1,le):
        a2 = a[i]
        n2=n[i]
        if not merge(a1,n1,a2,n2):
            return -1
        a1 = a3
        n1 = n3
    return (a1,n1)


n =  [p,q]
c =  [pow(c1,(p+1)//4,p),pow(c1,(q+1)//4,q)]
m =exCRT(c,n)
print(long_to_bytes(m))

n =  [p,q]
c =  [pow(c1,(p+1)//4,p),-pow(c1,(q+1)//4,q)]
m =exCRT(c,n)
print(long_to_bytes(m))

n =  [p,q]
c =  [-pow(c1,(p+1)//4,p),pow(c1,(q+1)//4,q)]
m =exCRT(c,n)
print(long_to_bytes(m))

n =  [p,q]
c =  [-pow(c1,(p+1)//4,p),-pow(c1,(q+1)//4,q)]
m =exCRT(c,n)
print(long_to_bytes(m))

#flag{r4b1n#4c58}

小明的密码题

题目描述：

小明正在完成课后作业, 但是屏幕的某一块地方被墨水涂黑了(我们不妨假设小明无法擦去墨水, 并且该电脑是一个真空中的球形电脑)

题目：

from Crypto.Util.number import *
from secret import *
flag_part = flag_content + '#' + secret_token
p = getPrime(512)
q = getPrime(512)

m = bytes_to_long(flag_part.encode())

e = 5
n = p*q

c = pow(m,e,n)

print('n =', n)
print('c =', c)
print('flag_part =', flag_part)
print()
print('--- hint begin ---')
print('flag = "flag{" + flag_part + "}"')
print('type of secret_token is', type(secret_token))
print('length of secret_token is', len(secret_token))

# n = 131889193322687215946601811511407251196213571687093913054335139712633125177496800529685285401802802683116451016274353008428347997732857844896393358010946452397522017632024075459908859131965234835870443110233375074265933004741459359128684375786221535003839961829770182916778717973782408036072622166388614214899
# c = 11188201757361363141578235564807411583085091933389381887827791551369738717117549969067660372214366275040055647621817803877495473068767571465521881010707873686036336475554105314475193676388608812872218943728455841652208711802376453034141883236142677345880594246879967378770573385522326039206400578260353074379
# flag_part = sm4ll_r00ts_is_brilliant#◼️◼️◼️◼️◼️◼️◼️◼️
# 
# --- hint begin ---
# flag = "flag{" + flag_part + "}"
# type of secret_token is <class 'str'>
# length of secret_token is 8

已知m高位攻击，构造的多项式如下：

$$f(x) = (m_{high} + x)^5 - c \quad (mod\;n)$$

x为未知的m低位小根，smallroots求解该多项式即可。

exp：

from Crypto.Util.number import *

n = 131889193322687215946601811511407251196213571687093913054335139712633125177496800529685285401802802683116451016274353008428347997732857844896393358010946452397522017632024075459908859131965234835870443110233375074265933004741459359128684375786221535003839961829770182916778717973782408036072622166388614214899
c = 11188201757361363141578235564807411583085091933389381887827791551369738717117549969067660372214366275040055647621817803877495473068767571465521881010707873686036336475554105314475193676388608812872218943728455841652208711802376453034141883236142677345880594246879967378770573385522326039206400578260353074379
m = bytes_to_long(b"sm4ll_r00ts_is_brilliant#" + b"\x00"*8)

PR.<x> = PolynomialRing(Zmod(n))
f = (m + x)^5 - c
f = f.monic()
roots = f.small_roots(X = 2^64)

m = m + int(roots[0])
print(long_to_bytes(m))

#flag{sm4ll_r00ts_is_brilliant#cc0dac72}

babyrandom

题目描述：

一个简易的LCG随机数生成器

题目：

#!/usr/bin/python3
from secret import flag
from Crypto.Util.number import *
from random import randrange

p = 64999433139797068147576269731948390094958654326970231465808792590598519729077

a = randrange(2, p)
b = randrange(2, p)
x = bytes_to_long(flag)
menu = '''

Random as a Service with LCG backend

Enter your option
1. Reset
2. Get
3. Exit
'''

def GetRandom():
    global x
    nx = (a*x + b) % p
    print(nx)
    x = nx
    
while True:
    print(menu)
    opt = input('> ')
    try:
        opt = int(opt)
        if opt == 1:
            x = bytes_to_long(flag)
        elif opt == 2:
            GetRandom()
        elif opt == 3:
            break
        else:
            print('invalid option')
    except Exception as e:
        print('oh no, something wrong!')
        print(e)

其实就是一个未知a、b的LCG，只是换成了交互题。先发送1设置种子为flag，再发送2申请三组未知数即可还原参数a、b，进而得到种子flag。

exp：

from Crypto.Util.number import *
from pwn import *

#context.log_level = 'debug'

r = remote("node4.buuoj.cn", 29676)
r.recvuntil(b"> ")
r.sendline(b"1")

c = []
for i in range(3):
    r.recvuntil(b"> ")
    r.sendline(b"2")
    c.append(int(r.recvline().strip().decode()))

p = 64999433139797068147576269731948390094958654326970231465808792590598519729077
c1,c2,c3 = c

a = inverse(c2-c1,p)*(c3-c2) %p
b = (-a*c1 + c2) % p

temp = c1
temp = ((temp - b) * inverse(a,p)) % p
print(long_to_bytes(temp))

#flag{lcg_1s_n0t_s3cur3#fb528ba5}

knapsack

题目描述：

来自ASIS Quals 的背包密码题

题目：

import random
import gmpy2
from Crypto.Util.number import *
from secret import flag
import codecs

m = [int(i) for i in bin(int(codecs.encode(flag,  'hex'), 16))[2:]]

# from ASIS Cyber Security Contest Quals 2014
def makeKey(n):
    privKey = [random.randint(1, 4**n)]
    s = privKey[0]
    for i in range(1, n):
        privKey.append(random.randint(s + 1, 4**(n + i)))
        s += privKey[i]
    q = random.randint(privKey[n-1] + 1, 2*privKey[n-1])
    r = random.randint(1, q)
    while gmpy2.gcd(r, q) != 1:
        r = random.randint(1, q)
    pubKey = [ r*w % q for w in privKey ]
    return privKey, q, r, pubKey

priv, q, r, pub = makeKey(len(m))

ciphertext = sum([i*j for i, j in zip(pub, m)])

print(ciphertext)
print(pub)

作为ctf wiki讲解背包加密的例题，其经典性无需多言：

背包加密 - CTF Wiki (ctf-wiki.org)

exp：

from Crypto.Util.number import *
c = 
b = 
'''
n = len(b)
L = Matrix(ZZ, n+1, n+1)

for i in range(n):
    L[i,i] = 1
    L[i,-1] = b[i]
L[-1,-1] = -c

res = L.LLL()

for i in range(n + 1):
    M = res.row(i).list()
    flag = True
    for m in M:
        if m != 0 and m != 1:
            flag = False
            break
    if flag:
        print(i, M)
'''

flag =  [1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0]
flag = int(''.join(list(map(str, flag[:-1]))), 2)

print(long_to_bytes(flag))

#flag{Lattice_reduction#c3662541}

Door

题目描述：

你被锁在了自然哲学学院里面, 想办法逃出来吧

题目：

from secret import flag
import string
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
from os import urandom
import re

key = urandom(16)

menu = '''
[+] WatchDog Security System
[+] Copyright (c) 1010 by School of Natural Philosophy 

please select your option:
1. Unlock Secret Entry
2. Help
3. Exit
'''

valid_code = [1033,3329,4431,5052]

auth_context_pattern = re.compile(r'^SoNP#[0-9]{4}$')

def auth_context_checker(ctx : bytes):
    for c in ctx:
        if chr(c) not in string.printable:
            return False
    if auth_context_pattern.match(ctx.decode()) : return True

    return False

def unlock():
    token = bytes.fromhex(input('Enter your token > '))
    auth_code = bytes.fromhex(input('Enter your authentication code > '))

    cipher = AES.new(key, AES.MODE_CBC,token)
    
    check = cipher.decrypt(auth_code)
    try:
        
        msg = unpad(check, 16)
        if auth_context_checker(msg) and int(msg[5:].decode()) in valid_code:
            print('door unlocked, here is your reward')
            print(flag)
        else:
            print('get out')

    except Exception as e:
        print('oops, something wrong')
        print(e)
def help():
    print('To unlock the door, please enter your token and authentication code.')
while True:
    print(menu)
    opt = input('> ')
    try:
        opt = int(opt)
        if opt == 1:
            unlock()
        elif opt == 2:
            help()
        elif opt == 3:
            break
        else:
            print('invalid option')
    except:
        print('oh no, something wrong!')

CBC模式的预言填充攻击，这是我从Xenny师傅的密码工坊里学到的我觉得很有意思的一种攻击方式，所以在这里展开说一说。

首先看看靶机能够提供什么样的功能，首先，在与靶机连接后，靶机生成一个16字节的随机串作为AES的密钥key，然后可以：

• 选择1，可以输入两段十六进制串，分别是token和auth_code。靶机将会把token作为AES中CBC模式的iv向量，将auth_code作为密文进行解密。
• 在成功解密之后，靶机将尝试对密文进行解填充，如果解填充失败，将会输出”oops, something wrong”
• 如果解填充成功，靶机将会对解密得到的明文进行核验，核验要求：1、明文为”SoNP#”+4个数字的字符串的形式；2、四个数字需要是valid_code中的其中之一。
• 通过核验，则得到flag；通不过核验，则输出”get out”

那么分几个部分讲一下如何进行这个攻击。

解填充

很重要的一点是，解密出来的明文通不过核验，和解填充失败，靶机输出的信息分别是”get out”和”oops, something wrong”，这个区别是很重要的。那么到底针对一个明文是如何解填充的呢？查看unpad源码可以知道，pad和unpad函数默认使用的是PKCS7的填充模式。

在这个模式下，如果最后一组明文长度为15，就需要填充一字节的b”\x01”；如果为14，就需要填充两字节的b”\x02”，以此类推。需要注意的是，当明文恰好为16的整数倍时，仍然需要填充16字节的b”\x10”，这是为了在解密时能正确地识别填充字节。

可以发现，以这种方式填充，填充后的明文会有一个很重要的特性：

• 填充后的明文的最后一字节等于填充的字节的长度

因此，明文只要满足上述特性，就能正确解填充。

预言填充攻击

那么如何利用解填充的这个特性进行CBC模式下的预言填充攻击呢？我们先画一个只有一个分组的CBC模式解密图示：

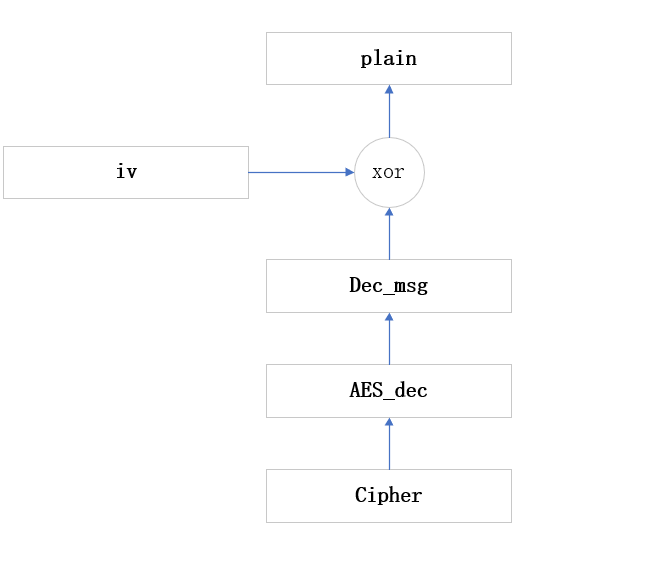
其中，cipher是我们输入的auth_code，iv是我们输入的token。cipher经AES解密后，得到dec_msg，并与iv异或后得到plain，也就是题目中的msg。

由于密钥key随机且未知，因此我们不管输入什么auth_code，我们都没有办法获得dec_msg的具体值。然而，dec_msg需要和iv异或，而iv是我们自行输入的。因此我们完全可以固定cipher，调整iv，来改变最终解密得到的plain。

那么我们假设某一次输入的cipher，iv，解密后得到的恰好是下面这样的plain：

b"justatest\x07\x07\x07\x07\x07\x07\x07"

可以看到，他满足PKCS7的填充模式，因此unpad是可以正确解密的。而我们可以调整iv的最后一字节，从而对应改变plain的最后一字节，这样他就无法正确解填充了。

然而，在某一个特殊的iv下，他仍然能正确解密，这也是我们进行攻击的根本依据。想一想在什么时候他仍然会正确解填充？

其实就是当我们输入的iv使得明文变成下面这样时：

b"justatest\x07\x07\x07\x07\x07\x07\x01"

这也是满足PKCS7填充模式的吧！所以当iv使得plain变成上面这种形式时，靶机会返回”get out”，而不是”oops, something wrong”。而这为我们也带来了一个很重要的信息，也就是dec_msg的最后一字节的值，就等于当前iv的最后一字节异或b”\x01”的值。

在这之后呢，我们将iv的最后一字节对应修改一下，使得其解密得到的plain最后一字节变成b”\x02”，接下来就如法炮制，爆破iv的倒数第二个字节，使得明文为：

b"justatest\x07\x07\x07\x07\x07\x02\x02"

此时也可以正确解填充，对应的，dec_msg的倒数第二个字节值就为当前iv的倒数第二个字节异或b”\x02”的值。

那么接下来就是对剩下十四个字节按这个方式逐个爆破，就能获得完整的dec_msg，而此时我们取token为dec_msg异或需要的msg值，就可以解密出我们需要的明文值，从而得到flag了。

exp：

from Crypto.Util.number import *
from pwn import *
from tqdm import *
from Crypto.Util.Padding import pad

#context.log_level = 'debug'

valid_code = [1033,3329,4431,5052]

r = remote("node4.buuoj.cn", 28412)

dec_list = [0 for i in range(16)]
use_list = [0 for i in range(16)]
auth_code = (b"\x00"*16).hex().encode()

for j in range(16):
    for i in trange(256):
        r.recvuntil(b"> ")
        r.sendline(b"1")
        r.recvuntil(b"token > ")

        temp1 = b""
        for k in use_list[:15-j]:
            temp1 += long_to_bytes(k)
        temp2 = b""
        for k in use_list[15-j+1:]:
            temp2 += long_to_bytes(k)
        change_byte = long_to_bytes(i)
        token = (temp1 + change_byte + temp2).hex().encode()

        r.sendline(token)
        r.recvuntil(b"code > ")
        r.sendline(auth_code)

        temp = r.recvline()
        if(b"get out" in temp):
            dec_list[15-j] = i ^ (j+1)
            for k in range(j+1):
                use_list[15-k] = dec_list[15-k] ^ (j+2)
            break

#getflag
final = bytes_to_long(pad(b"SoNP#1033",16))
temp = b""
for k in dec_list:
    temp += long_to_bytes(k)
temp = final ^ bytes_to_long(temp)
final_token = long_to_bytes(temp).hex().encode()
r.recvuntil(b"> ")
r.sendline(b"1")
r.recvuntil(b"token > ")
r.sendline(final_token)
r.recvuntil(b"code > ")
r.sendline(auth_code)
temp = r.recvline()
temp = r.recvline()
print(temp)

#flag{d0_n0t_3xpose_th3_padd1ng_5tatus}

eazy_crt

题目：

from Crypto.Util.number import *
from secret import flag, p, q
from hashlib import *
import random

assert 'flag{' + md5(str(p).encode()).hexdigest() + '}' == flag
assert isPrime(p), isPrime(q)
assert p.bit_length() == 1024, q.bit_length() == 1024

m = random.getrandbits(400)
e = 65537
d = inverse(e, (p - 1) * (q - 1))
r1, r2, r3 = getPrime(20), getPrime(20), getPrime(10)

dp, dq = d % (p - 1), d % (q - 1)
Sp, Sq = pow(m + getPrime(10), dp, r1 * p), pow(m, dq, r2 * q)
s1, s2 = pow(m, dp % (r1 - 1), r1), pow(m, dq % (r2 - 1), r2)
S_ = Sq + (q * r2) * (int(inverse(q * r2, p * r1)) * (Sp - Sq) % (p * r1))
c1, c2 = (S_ - s1 + 1) % r1, (S_ - s2 + 1) % r2
gamma = (r3 * c1 + (2 ** 10 - r3) * c2) // (2 ** 10)
S = pow(S_, gamma, p * q)

print(m)
print(p * q)
print(S_)
print(S)

'''
m=2180240512138982889935733758776025289492848542072999905411903898302427496814336475436552230920326681809745778470583226987
n=25505131259827344749407187081729819350996141100990518281765117676936124636084125400315049858697199427401342785804654120926568235761577895862889807660442415521870277729420875825744007886870384790308986342360349597392841568418588521694478184632631896474390291958350681472768485356865513284619086754437723630874827593280089682939629265210875169009057935264259019861755270570945614034505771690412042781423771110441028258110022746603974882162934979726300741541857444013708508946471384525030286343828680432038605288717842755346907256658746733811881247992925881684393431852248253701825024590345480994598867741811599162649467
S_=5510086561842250138908875342533294108331951659612671466695801343686972919443402163401521040457640602756777910081639191753436122171756174730531385913865951826869995984787102439679170684422717808771260217541439878677750508065703064081375473845405916674327932798153100574555933448570618732842365795738120491532398081467312017203933413296779070611024124965772787502242499016884537233028947865288037718074352448773759363242111080540630360902388540661831992776707600133253329779003707938065020121645530719140954554800986771763343191398210100325971573069812381693089384221441735278736889673500218274673196333806222266248844379127652366
S=11422623501509574650959962952004985925543723972567988534433510888436662069119800576321679344425052011563473005275801787271861671898318523033415642388512047035650991047953319601346912194462122313366888126100093635969476696871403883687946617575837061694813669883782221006701704487938500886952347003631626326127154081787016692856628561200386941683756397734100698520464199249811238013146899352390453500132666840606585760306723894654933077094375810666168464835756607377998959675132305971721109661644231613426322675350973373434138686086023265910883509514575554429502214217460059521619625693750938117427832654792355808803321
'''

题目改编自广东强网杯2021的easycrt，并且这一题给出了S，更加简单。具体题解见我的另一篇博客：

Crypto趣题-RSA | 糖醋小鸡块的blog (tangcuxiaojikuai.xyz)

exp：

from Crypto.Util.number import *
from hashlib import *
from tqdm import *

m=2180240512138982889935733758776025289492848542072999905411903898302427496814336475436552230920326681809745778470583226987
n=25505131259827344749407187081729819350996141100990518281765117676936124636084125400315049858697199427401342785804654120926568235761577895862889807660442415521870277729420875825744007886870384790308986342360349597392841568418588521694478184632631896474390291958350681472768485356865513284619086754437723630874827593280089682939629265210875169009057935264259019861755270570945614034505771690412042781423771110441028258110022746603974882162934979726300741541857444013708508946471384525030286343828680432038605288717842755346907256658746733811881247992925881684393431852248253701825024590345480994598867741811599162649467
S_=5510086561842250138908875342533294108331951659612671466695801343686972919443402163401521040457640602756777910081639191753436122171756174730531385913865951826869995984787102439679170684422717808771260217541439878677750508065703064081375473845405916674327932798153100574555933448570618732842365795738120491532398081467312017203933413296779070611024124965772787502242499016884537233028947865288037718074352448773759363242111080540630360902388540661831992776707600133253329779003707938065020121645530719140954554800986771763343191398210100325971573069812381693089384221441735278736889673500218274673196333806222266248844379127652366
S=11422623501509574650959962952004985925543723972567988534433510888436662069119800576321679344425052011563473005275801787271861671898318523033415642388512047035650991047953319601346912194462122313366888126100093635969476696871403883687946617575837061694813669883782221006701704487938500886952347003631626326127154081787016692856628561200386941683756397734100698520464199249811238013146899352390453500132666840606585760306723894654933077094375810666168464835756607377998959675132305971721109661644231613426322675350973373434138686086023265910883509514575554429502214217460059521619625693750938117427832654792355808803321

c2 = 1
c1 = pow(S,65537,n)
q = GCD(pow(S_,65537,n)-m,n)
p = n // q
print(p)
print('flag{' + md5(str(p).encode()).hexdigest() + '}')

#flag{b40ea076da8c73572ae5d067aa0fc22e}

Week 4

第四周题目其实我觉得比第三周更容易一点。

RSA Variation II

题目描述：

"Schmidt Samoa"

题目：

from secret import flag
from Crypto.Util.number import *

p = getPrime(1024)
q = getPrime(1024)

N = p*p*q

d= inverse(N, (p-1)*(q-1)//GCD(p-1, q-1))

m = bytes_to_long(flag)

c = pow(m, N, N)

print('c =', c)
print('N =', N)
print('d =', d)

# c = 1653396627113549535760516503668455111392369905404419847336187180051939350514408518095369852411718553340156505246372037811032919080426885042549723125598742783778413642221563616358386699697645814225855089454045984443096447166740882693228043505960011332616740785976743150624114653594631779427044055729185392854961786323215146318588164139423925400772680226861699990332420246447180631417523181196631188540323779487858453719444807515638025771586275969579201806909799448813112034867089866513864971414742370516244653259347267231436131850871346106316007958256749016599758599549180907260093080500469394473142003147643172770078092713912200110043214435078277125844112816260967490086038358669788006182833272351526796228536135638071670829206746835346784997437044707950580087067666459222916040902038574157577881880027391425763503693184264104932693985833980182986816664377018507487697769866530103927375926578569947076633923873193100147751463
# N = 1768427447158131856514034889456397424027937796617829756303525705316152314769129050888899742667986532346611229157207778487065194513722005516611969754197481310330149721054855689646133721600838194741123290410384315980339516947257172981002480414254023253269098539962527834174781356657779988761754582343096332391763560921491414520707112852896782970123018263505426447126195645371941116395659369152654368118569516482251442513192892626222576419747048343942947570016045016127917578272819812760632788343321742583353340158009324794626006731057267603803701663256706597904789047060978427573361035171008822467120148227698893238773305320215769410594974360573727150122036666987718934166622785421464647946084162895084248352643721808444370307254417501852264572985908550839933862563001186477021313236113690793843893640190378131373214104044465633483953616402680853776480712599669132572907096151664916118185486737463253559093537311036517461749439
# d = 20650646933118544225095544552373007455928574480175801658168105227037950105642248948645762488881219576174131624593293487325329703919313156659700002234392400636474610143032745113473842675857323774566945229148664969659797779146488402588937762391470971617163496433008501858907585683428652637958844902909796849080799141999490231877378863244093900363251415972834146031490928923962271054053278056347181254936750536280638321211545167520935870220829786490686826062142415755063724639110568511969041175019898031990455911525941036727091961083201123910761290998968240338217895275414072475701909497518616112236380389851984377079

题目已经告知是Schmidt Samoa加密方式，其加密流程类似RSA却又有不同，具体如下：

$$N = p^2q$$ $$e = N$$ $$d \equiv e^{-1} \quad (mod\;\phi(pq))$$

其加密为：

$$c \equiv m^N \quad(mod\;N)$$

解密为：

$$m \equiv c^d \quad(mod\;pq)$$

之所以可以正确解密是因为：

$$c^d \equiv m^{Nd} \equiv m^{1+\phi(pq)} \equiv m \quad(mod\;pq)$$

而现在我们有N和d，则由解密流程知道，对于任意x，有：

$$x^{Nd} \equiv x \quad(mod\;pq)$$

因此有：

$$gcd(x^{Nd}-x,n) = pq$$

然后我们就能得到pq，就可以用他的解密方法解密得到明文了。

exp：

from Crypto.Util.number import *

c = 1653396627113549535760516503668455111392369905404419847336187180051939350514408518095369852411718553340156505246372037811032919080426885042549723125598742783778413642221563616358386699697645814225855089454045984443096447166740882693228043505960011332616740785976743150624114653594631779427044055729185392854961786323215146318588164139423925400772680226861699990332420246447180631417523181196631188540323779487858453719444807515638025771586275969579201806909799448813112034867089866513864971414742370516244653259347267231436131850871346106316007958256749016599758599549180907260093080500469394473142003147643172770078092713912200110043214435078277125844112816260967490086038358669788006182833272351526796228536135638071670829206746835346784997437044707950580087067666459222916040902038574157577881880027391425763503693184264104932693985833980182986816664377018507487697769866530103927375926578569947076633923873193100147751463
n = 1768427447158131856514034889456397424027937796617829756303525705316152314769129050888899742667986532346611229157207778487065194513722005516611969754197481310330149721054855689646133721600838194741123290410384315980339516947257172981002480414254023253269098539962527834174781356657779988761754582343096332391763560921491414520707112852896782970123018263505426447126195645371941116395659369152654368118569516482251442513192892626222576419747048343942947570016045016127917578272819812760632788343321742583353340158009324794626006731057267603803701663256706597904789047060978427573361035171008822467120148227698893238773305320215769410594974360573727150122036666987718934166622785421464647946084162895084248352643721808444370307254417501852264572985908550839933862563001186477021313236113690793843893640190378131373214104044465633483953616402680853776480712599669132572907096151664916118185486737463253559093537311036517461749439
d = 20650646933118544225095544552373007455928574480175801658168105227037950105642248948645762488881219576174131624593293487325329703919313156659700002234392400636474610143032745113473842675857323774566945229148664969659797779146488402588937762391470971617163496433008501858907585683428652637958844902909796849080799141999490231877378863244093900363251415972834146031490928923962271054053278056347181254936750536280638321211545167520935870220829786490686826062142415755063724639110568511969041175019898031990455911525941036727091961083201123910761290998968240338217895275414072475701909497518616112236380389851984377079

pq = GCD(pow(2,n*d,n)-2,n)
m = pow(c,d,pq)
print(long_to_bytes(m))

#flag{l3arn_s0m3_e1ement4ry_numb3r_the0ry}

babyNTRU

题目描述：

NTRU, 但是只有常数项

题目：

from secret import flag
from Crypto.Util.number import *

q = getPrime(2048)

f = getPrime(1024)
g = getPrime(768)

h = (inverse(f, q) * g) % q

m = bytes_to_long(flag)

e = (getPrime(32) * h + m) % q

print((h, q))
print(e)

# (8916452722821418463248726825721257021744194286874706915832444631771596616116491775091473142798867278598586482678387668986764461265131119164500473719939894343163496325556340181429675937641495981353857724627081847304246987074303722642172988864138967404024201246050387152854001746763104417773214408906879366958729744259612777257542351501592019483745621824894790096639205771421560295175633152877667720038396154571697861326821483170835238092879747297506606983322890706220824261581533324824858599082611886026668788577757970984892292609271082176311433507931993672945925883985629311514143607457603297458439759594085898425992, 31985842636498685945330905726539498901443694955736332073639744466389039373143618920511122288844282849407290205804991634167816417468703459229138891348115191921395278336695684210437130681337971686008048054340499654721317721241239990701099685207253476642931586563363638141636011941268962999641130263828151538489139254625099330199557503153680089387538863574480134898211311252227463870838947777479309928195791241005127445821671684607237706849308372923372795573732000365072815112119533702614620325238183899266147682193892866330678076925199674554569018103164228278742151778832319406135513140669049734660019551179692615505961)
# 20041713613876382007969284056698149007154248857420752520496829246324512197188211029665990713599667984019715503486507126224558092176392282486689347953069815123212779090783909545244160318938357529307482025697769394114967028564546355310883670462197528011181768588878447856875173263800885048676190978206851268887445527785387532167370943745180538168965461612097037041570912365648125449804109299630958840398397721916860876687808474004391843869813396858468730877627733234832744328768443830669469345926766882446378765847334421595034470639171397587395341977453536859946410431252287203312913117023084978959318406160721042580688

格入门时肯定会见过的一个题目，这里不做阐述了。

exp：

from Crypto.Util.number import *

h,q = (8916452722821418463248726825721257021744194286874706915832444631771596616116491775091473142798867278598586482678387668986764461265131119164500473719939894343163496325556340181429675937641495981353857724627081847304246987074303722642172988864138967404024201246050387152854001746763104417773214408906879366958729744259612777257542351501592019483745621824894790096639205771421560295175633152877667720038396154571697861326821483170835238092879747297506606983322890706220824261581533324824858599082611886026668788577757970984892292609271082176311433507931993672945925883985629311514143607457603297458439759594085898425992, 31985842636498685945330905726539498901443694955736332073639744466389039373143618920511122288844282849407290205804991634167816417468703459229138891348115191921395278336695684210437130681337971686008048054340499654721317721241239990701099685207253476642931586563363638141636011941268962999641130263828151538489139254625099330199557503153680089387538863574480134898211311252227463870838947777479309928195791241005127445821671684607237706849308372923372795573732000365072815112119533702614620325238183899266147682193892866330678076925199674554569018103164228278742151778832319406135513140669049734660019551179692615505961)
e = 20041713613876382007969284056698149007154248857420752520496829246324512197188211029665990713599667984019715503486507126224558092176392282486689347953069815123212779090783909545244160318938357529307482025697769394114967028564546355310883670462197528011181768588878447856875173263800885048676190978206851268887445527785387532167370943745180538168965461612097037041570912365648125449804109299630958840398397721916860876687808474004391843869813396858468730877627733234832744328768443830669469345926766882446378765847334421595034470639171397587395341977453536859946410431252287203312913117023084978959318406160721042580688

L = Matrix(ZZ, [[1, h],
                [0, q]])

f, g = L.LLL()[0]

m = (f*e) % q % g * inverse_mod(f, g) % g

print(long_to_bytes(m))

#flag{Lattice_reduction_magic_on_NTRU#82b08b2d}

Smart

题目描述：

一个解决ECDLP的好方法

题目：

from Crypto.Util.number import *
from sage.all import *
from secret import flag

p = 75206427479775622966537995406541077245842499523456803092204668034148875719001
a = 40399280641537685263236367744605671534251002649301968428998107181223348036480
b = 34830673418515139976377184302022321848201537906033092355749226925568830384464

E = EllipticCurve(GF(p), [a, b])

d = bytes_to_long(flag)

G = E.random_element()

P = d * G

print(G)
print(P)

# (63199291976729017585116731422181573663076311513240158412108878460234764025898 : 11977959928854309700611217102917186587242105343137383979364679606977824228558 : 1)
# (75017275378438543246214954287362349176908042127439117734318700769768512624429 : 39521483276009738115474714281626894361123804837783117725653243818498259351984 : 1)

题目标题明示Smart attack，那么也不需要检查曲线阶是否等于p了，直接Smart attack就好。

exp：

from Crypto.Util.number import *
from hashlib import md5

def MD5(m):return md5(str(m).encode()).hexdigest()

p = 75206427479775622966537995406541077245842499523456803092204668034148875719001
a = 40399280641537685263236367744605671534251002649301968428998107181223348036480
b = 34830673418515139976377184302022321848201537906033092355749226925568830384464
G = (63199291976729017585116731422181573663076311513240158412108878460234764025898 , 11977959928854309700611217102917186587242105343137383979364679606977824228558)
dG = (75017275378438543246214954287362349176908042127439117734318700769768512624429 , 39521483276009738115474714281626894361123804837783117725653243818498259351984)

E = EllipticCurve(GF(p),[a,b])

P = E(G)
Q = E(dG)

def SmartAttack(P,Q,p):
    E = P.curve()
    Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])

    P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
    for P_Qp in P_Qps:
        if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
            break

    Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
    for Q_Qp in Q_Qps:
        if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
            break

    p_times_P = p*P_Qp
    p_times_Q = p*Q_Qp

    x_P,y_P = p_times_P.xy()
    x_Q,y_Q = p_times_Q.xy()

    phi_P = -(x_P/y_P)
    phi_Q = -(x_Q/y_Q)
    k = phi_Q/phi_P
    return ZZ(k)

d = int(SmartAttack(P, Q, p))

print(long_to_bytes(int(d)))

#flag{m1nd_y0ur_p4rameter#167d}

signin

题目描述：

签个道吧

题目：

from Crypto.Util.number import isPrime,bytes_to_long, sieve_base
from random import choice
from secret import flag

m=bytes_to_long(flag)
def uniPrime(bits):
    while True:
        n = 2
        while n.bit_length() < bits:
            n *= choice(sieve_base)
        if isPrime(n + 1):
            return n + 1


p=uniPrime(512)
q=uniPrime(512)
n=p*q
e= 196608
c=pow(m,e,n)

print("n=",n)
print("c=",c)

'''
n= 3326716005321175474866311915397401254111950808705576293932345690533263108414883877530294339294274914837424580618375346509555627578734883357652996005817766370804842161603027636393776079113035745495508839749006773483720698066943577445977551268093247748313691392265332970992500440422951173889419377779135952537088733
c= 2709336316075650177079376244796188132561250459751152184677022745551914544884517324887652368450635995644019212878543745475885906864265559139379903049221765159852922264140740839538366147411533242116915892792672736321879694956051586399594206293685750573633107354109784921229088063124404073840557026747056910514218246
'''

可以发现素数的生成方式均满足p-1光滑，因此可以求出p、q。然后发现：

$$e = 2^{16}*3$$

那么预期应该是先求出3的逆元，然后高次Rabin解。不过最近才新学了一招nth_root，试验一下发现真行，这函数很舒服。

exp：

from Crypto.Util.number import *
from sympy.ntheory.modular import crt

n= 3326716005321175474866311915397401254111950808705576293932345690533263108414883877530294339294274914837424580618375346509555627578734883357652996005817766370804842161603027636393776079113035745495508839749006773483720698066943577445977551268093247748313691392265332970992500440422951173889419377779135952537088733
c= 2709336316075650177079376244796188132561250459751152184677022745551914544884517324887652368450635995644019212878543745475885906864265559139379903049221765159852922264140740839538366147411533242116915892792672736321879694956051586399594206293685750573633107354109784921229088063124404073840557026747056910514218246
#e = 2^16*3
e= 196608

#smooth p-1
'''
a = 2
m = 2
while True:
    a = pow(a, m, n)
    p = GCD(a-1, n)
    if p != 1 and p != n:
        break
    m += 1

q = n // p
print(p)
print(q)
'''
p = 11104262127139631006017377403513327506789883414594983803879501935187577746510780983414313264114974863256190649020310407750155332724309172387489473534782137699
q = 299589109769881744982450090354913727490614194294955470269590615599558785111624291036465332556249607131912597764625231248581361283506625311199114064303807167

dp = inverse(3,p-1)
dq = inverse(3,q-1)
cp = pow(c,dp,p)
cq = pow(c,dq,q)

F = Zmod(p)
cp = F(cp)
resp = cp.nth_root(2^16,all=True)

F = Zmod(q)
cq = F(cq)
resq = cq.nth_root(2^16,all=True)

for i in resp:
    for j in resq:
        mod = [p,q]
        c = [int(i),int(j)]
        m = crt(mod,c)[0]
        if(b"flag" in long_to_bytes(m)):
            print(long_to_bytes(m))

#flag{new1sstar_welcome_you}

error

题目描述：

从错误中学习

题目：

from sage.all import *
from secret import flag
import random
data = [ord(x) for x in flag]

mod = 0x42
n = 200
p = 5
q = 2**20

def E():
  return vector(ZZ, [1 - random.randint(0,p) for _ in range(n)])

def creatematrix():
  return matrix(ZZ, [[q//2 - random.randint(0,q) for _ in range(n)] for _ in range(mod)])

A, B, C= creatematrix(), creatematrix(), creatematrix()
x = vector(ZZ, data[0:mod])
y = vector(ZZ, data[mod:2*mod])
z = vector(ZZ, data[2*mod:3*mod])
e = E()
b = x*B+y*A+z*C + e
res = ""
res += "A=" + str(A) +'\n'
res += "B=" + str(B) +'\n'
res += "C=" + str(C) +'\n'
res += "b=" + str(b) +'\n'

with open("enc.out","w") as f:
  f.write(res)

题目描述与标题都说明这是一个LWE(Learning With Errors)问题，不过这道题目自己造格也很容易，这里还是先梳理一下题目加密流程。

• 将flag每个字符的ASCII码存储到列表data中，并将data分为长度相等的三段，分别作为向量x、y、z
• 生成三个随机矩阵A、B、C，其大小均为mod*n，其中元素为(-q/2,q/2)之间的随机数
• 生成一个误差向量e，其元素为(-4,1)的随机数
• 计算向量b，满足：

b = x*B+y*A+z*C + e

• 给出A、B、C、b，要求还原flag

由于flag的ASCII码被存在列表data中，而data又被分为三段向量x、y、z，因此本题其实就是要还原x、y、z向量。而我们拥有的等量关系是：

b = x*B+y*A+z*C + e

把他展开写为直观形式：

$$(b_1,b_2,...b_n) = (x_1,x_2,...x_{mod})* \left( \begin{matrix} A_{1,1}&A_{1,2}& &\\ A_{2,1}&A_{2,2}& &\\ & &... &\\ & & &A_{mod,n} \end{matrix} \right) + (y_1,y_2,...y_{mod})* \left( \begin{matrix} B_{1,1}&B_{1,2}& &\\ B_{2,1}&B_{2,2}& &\\ & &... &\\ & & &B_{mod,n} \end{matrix} \right) + (z_1,z_2,...z_{mod})* \left( \begin{matrix} C_{1,1}&C_{1,2}& &\\ C_{2,1}&C_{2,2}& &\\ & &... &\\ & & &C_{mod,n} \end{matrix} \right) + (e_1,e_2,...,e_n)$$

其实也就是下面的形式：

$$b = (x,y,z)* \left( \begin{matrix} A\\ B\\ C\\ \end{matrix} \right) + e$$

稍微移项变形一下：

$$-e = (x,y,z,-1)* \left( \begin{matrix} A\\ B\\ C\\ b\\ \end{matrix} \right)$$

而由于误差e是个很短的向量，那么以此关系就能构造一个格：

$$\left( \begin{matrix} A\\ B\\ C\\ b\\ \end{matrix} \right)$$

LLL就能规约得到向量e，然后解下面这个矩阵方程就能得到x、y、z，就能还原flag了：

$$b - e = (x,y,z)* \left( \begin{matrix} A\\ B\\ C\\ \end{matrix} \right)$$

实际上手操作时，由于sage矩阵的输出形式有点不尽人意，没办法直接读取，所以需要做一点处理。我的处理方式是：

• 新建一个空白matrix.txt文件
• 把enc.out的所有内容粘贴到matrix.txt文件中
• 将” “(四个空格)全局替换为”,”，再将” “(三个空格)全局替换为”,”，再将” “(两个空格)全局替换为”,”，再将” “(一个空格)全局替换为”,”
• 将”[,”全局替换为”[“，并在每个矩阵开头多加一个”[“，在每个矩阵结尾多加一个”]”
• 将”A=”、”B=”、”C=”、”b=”全部替换为”=”，主要是为了分隔几个矩阵
• 再进行一些可能进行的微调

然后就可以以如下方式读入矩阵和向量：

with open('matrix.txt','r') as f:
    data = f.read().split("=")
A = matrix(ZZ, eval(data[0].strip()))
B = matrix(ZZ, eval(data[1].strip()))
C = matrix(ZZ, eval(data[2].strip()))
b = vector(ZZ, eval(data[3].strip()))

其实用正则表达式来寻找每一行的所有数字应该会更方便，但是我不太会操作。

exp：

from Crypto.Util.number import *

with open('matrix.txt','r') as f:
    data = f.read().split("=")
A = matrix(ZZ, eval(data[0].strip()))
B = matrix(ZZ, eval(data[1].strip()))
C = matrix(ZZ, eval(data[2].strip()))
b = vector(ZZ, eval(data[3].strip()))

#LLL
L = block_matrix([[A],[B],[C],[matrix(b)]])
res = L.LLL()
e = vector(ZZ, res[0])

#getflag
coeffients = block_matrix([[A],[B],[C]])
flag = coeffients.solve_left(b-e)
for i in flag:
    print(chr(i),end = "")

#flag{try_lear1n_wi0h_t1e_error}

Week 5

last_signin

题目描述：

coppersmith可以帮助你

题目：

from Crypto.Util.number import *
flag = b'?'

e = 65537
p, q = getPrime(1024), getPrime(1024)
N = p * q
gift = p&(2**923-2**101)
m = bytes_to_long(flag)
c = pow(m, e, N)

print("N = ",N)
print("gift = ",gift)
print("c = ",c)

"""
N =  12055968471523053394851394038007091122809367392467691213651520944038861796011063965460456285088011754895260428814358599592032865236006733879843493164411907032292051539754520574395252298997379020268868972160297893871261713263196092380416876697472160104980015554834798949155917292189278888914003846758687215559958506116359394743135211950575060201887025032694825084104792059271584351889134811543088404952977137809673880602946974798597506721906751835019855063462460686036567578835477249909061675845157443679947730585880392110482301750827802213877643649659069945187353987713717145709188790427572582689339643628659515017749
p0 =  70561167908564543355630347620333350122607189772353278860674786406663564556557177660954135010748189302104288155939269204559421198595262277064601483770331017282701354382190472661583444774920297367889959312517009682740631673940840597651219956142053575328811350770919852725338374144
c =  2475592349689790551418951263467994503430959303317734266333382586608208775837696436139830443942890900333873206031844146782184712381952753718848109663188245101226538043101790881285270927795075893680615586053680077455901334861085349972222680322067952811365366282026756737185263105621695146050695385626656638309577087933457566501579308954739543321367741463532413790712419879733217017821099916866490928476372772542254929459218259301608413811969763001504245717637231198848196348656878611788843380115493744125520080930068318479606464623896240289381601711908759450672519228864487153103141218567551083147171385920693325876018
"""

这题前段时间也有个师傅问过我，其实是D3CTF的一道原题，wp如下：

D^3CTF 官方Write Up-安全客 - 安全资讯平台 (anquanke.com)

用wp中的exp可以进行这道题目的二元copper求解，而用普通的二元copper的话，不管是调参还是多爆破几位也出不来结果，具体原因就没研究过了。

exp：

from Crypto.Util.number import *

N =  12055968471523053394851394038007091122809367392467691213651520944038861796011063965460456285088011754895260428814358599592032865236006733879843493164411907032292051539754520574395252298997379020268868972160297893871261713263196092380416876697472160104980015554834798949155917292189278888914003846758687215559958506116359394743135211950575060201887025032694825084104792059271584351889134811543088404952977137809673880602946974798597506721906751835019855063462460686036567578835477249909061675845157443679947730585880392110482301750827802213877643649659069945187353987713717145709188790427572582689339643628659515017749
p0 =  70561167908564543355630347620333350122607189772353278860674786406663564556557177660954135010748189302104288155939269204559421198595262277064601483770331017282701354382190472661583444774920297367889959312517009682740631673940840597651219956142053575328811350770919852725338374144
c =  2475592349689790551418951263467994503430959303317734266333382586608208775837696436139830443942890900333873206031844146782184712381952753718848109663188245101226538043101790881285270927795075893680615586053680077455901334861085349972222680322067952811365366282026756737185263105621695146050695385626656638309577087933457566501579308954739543321367741463532413790712419879733217017821099916866490928476372772542254929459218259301608413811969763001504245717637231198848196348656878611788843380115493744125520080930068318479606464623896240289381601711908759450672519228864487153103141218567551083147171385920693325876018

def bivariate(pol, XX, YY, kk=4):
    N = pol.parent().characteristic()

    f = pol.change_ring(ZZ)
    PR, (x, y) = f.parent().objgens()

    idx = [(k - i, i) for k in range(kk + 1) for i in range(k + 1)]
    monomials = list(map(lambda t: PR(x ** t[0] * y ** t[1]), idx))
    # collect the shift-polynomials
    g = []
    for h, i in idx:
        if h == 0:
            g.append(y ** h * x ** i * N)
        else:
            g.append(y ** (h - 1) * x ** i * f)

    # construct lattice basis
    M = Matrix(ZZ, len(g))
    for row in range(M.nrows()):
        for col in range(M.ncols()):
            h, i = idx[col]
            M[row, col] = g[row][h, i] * XX ** h * YY ** i

    # LLL
    B = M.LLL()

    PX = PolynomialRing(ZZ, 'xs')
    xs = PX.gen()
    PY = PolynomialRing(ZZ, 'ys')
    ys = PY.gen()

    # Transform LLL-reduced vectors to polynomials
    H = [(i, PR(0)) for i in range(B.nrows())]
    H = dict(H)
    for i in range(B.nrows()):
        for j in range(B.ncols()):
            H[i] += PR((monomials[j] * B[i, j]) / monomials[j](XX, YY))

    # Find the root
    poly1 = H[0].resultant(H[1], y).subs(x=xs)
    poly2 = H[0].resultant(H[2], y).subs(x=xs)
    poly = gcd(poly1, poly2)
    x_root = poly.roots()[0][0]

    poly1 = H[0].resultant(H[1], x).subs(y=ys)
    poly2 = H[0].resultant(H[2], x).subs(y=ys)
    poly = gcd(poly1, poly2)
    y_root = poly.roots()[0][0]

    return x_root, y_root

PR = PolynomialRing(Zmod(N), names='x,y')
x, y = PR.gens()
pol = 2 ** 924 * x + y + p0

x, y = bivariate(pol, 2 ** 100, 2 ** 100)
p = 2 ** 924 * x + y + p0
q = N // p
e=65537
d = inverse(e, (p - 1)*(q - 1))
m = int(pow(c, d, N))
print(long_to_bytes(m))

#flag{although_11ts_norma11_tis_still_stay_dsadsa}

School of CRC32

题目描述：

来点CRC32挑战

题目：

import secrets
from secret import flag
import zlib

ROUND = 100

LENGTH = 20

print('Extreme hard CRC32 challenge')
print('ARE YOU READY')

for i in range(ROUND):
    print('ROUND', i, '!'*int(i/75 + 1))

    target = secrets.randbits(32)

    print('Here is my CRC32 value: ', hex(target))

    dat = input('Show me some data > ')
    raw = bytes.fromhex(dat)
    
    if zlib.crc32(raw) == target and len(raw) == LENGTH:
        print("GREAT")
    else:
        print("OH NO")
        exit()

print("Congratulation! Here is your flag")
print(flag)

题目要求进行一百轮挑战，全部通过就有flag，挑战的具体内容是：

• 生成32bit的随机数target，作为CRC32的目标值
• 输入一段长度为20的字节流，使得该字节流的CRC32值与给定target相等

当然可以去根据CRC的仿射与差分的相关性质去建立矩阵，然后求解矩阵方程得到碰撞。但是实际上知道有个轮子的话就很简单了：

crcsolver · PyPI

exp：

import crcsolver
from pwn import *
from tqdm import *

#context.log_level = 'debug'

sh = remote("node4.buuoj.cn",28240)

ROUND = 100
for i in trange(ROUND):
    sh.recvuntil(b"CRC32 value:  ")
    temp = eval(sh.recvline().strip().decode())
    cc = crcsolver.solve(b'_'*20, range(0,20*8), temp, binascii.crc32)
    raw = bytes.fromhex(cc.hex())
    sh.recvuntil(b"Show me some data > ")
    sh.sendline(cc.hex().encode())
sh.recvline()
sh.recvline()
print(sh.recvline())

#flag{a1gebra_i5_ma4ic#cf5d4a5d}

PseudoHell_EASY/PseudoHell_HARD

两个题其实共用一个附件，因此也放在一起说了

题目描述：

欢迎来到随机天堂，来猜猜我投的硬币是1还是0吧

题目：

problems.py：

from challenge import Challenge1,Challenge2,Challenge3,Challenge4,Challenge5
from secret import flag_easy,flag_hard
roll_left = 56

def guess_coin(level, query_num):
    Ch = level()
    for _ in range(query_num):
        msg = bytes.fromhex(input("msg? > "))
        inverse = input("inverse? > ") == 'y'
        assert len(msg) == Ch.input_size
        print(Ch.roll(msg, inverse).hex())
    assert input("coin? > ") == str(Ch.coin) 

def roll_challenge(challenge_level, challenge):
    global roll_left
    print(f"[+] Challenge Level: {challenge_level}")
    roll_num = int(input(f"How many times are required to roll for solving {challenge_level}? > "))
    roll_left -= roll_num
    [guess_coin(challenge, roll_num) for _ in range(33)]

roll_challenge("1", Challenge1)
roll_challenge("2", Challenge2)
roll_challenge("3", Challenge3)

if roll_left <= 0:
    print("You passed all challenges for EASY but times limit exceeded. Try harder :(")
    exit(-1)

print("flag for easy is ", flag_easy)

roll_challenge("4", Challenge4)
roll_challenge("5", Challenge5)

if roll_left <= 0:
    print("You passed all challenges for HARD but times limit exceeded. Try harder :(")
    exit(-1)

print("flag for hard is ", flag_hard)

challenge.py：

import os
def xor(a:bytes,b:bytes):
    assert len(a) == len(b)
    return bytes([i ^ j for i,j in zip(a,b)])

class PRP():
    def __init__(self, n):
        self.domain_cache = {}
        self.range_cache = {}
        self.n = n

    def tran(self, m, inverse = False):
        if not inverse:
            x = m
            if x in self.domain_cache:
                return self.domain_cache[x]
            while True:
                y = os.urandom(self.n)
                if y in self.range_cache:continue
                self.domain_cache[x] = y
                self.range_cache[y] = x    
                return y
        else:
            y = m
            if y in self.range_cache:
                return self.range_cache[y]
            while True:
                x = os.urandom(self.n)
                if x in self.domain_cache:continue
                self.domain_cache[x] = y
                self.range_cache[y] = x    
                return x

class PRF():
    def __init__(self, n):
        self.domain_cache = {}
        self.range_cache = {}
        self.n = n 

    def tran(self, x):
        if x not in self.domain_cache:
            self.domain_cache[x] = os.urandom(self.n)
        return self.domain_cache[x]

class Challenge1:
    def __init__(self):
        self.coin = os.urandom(1)[0] & 1
        self.block_size = 8
        self.input_size = 2 * self.block_size
        self.RO1 = PRF(self.block_size)
        self.RO2 = PRF(self.input_size)

    def function1(self, M):
        L, R = M[:self.block_size], M[self.block_size:]
        L, R = R, xor(L, self.RO1.tran(R))
        return L+R

    def function2(self, M):
        return self.RO2.tran(M)

    def roll(self, M, inverse):
        assert inverse == False, "In Challenge1, inverse is not allowed"
        return [self.function1,self.function2][self.coin](M)

class Challenge2:
    def __init__(self):
        self.coin = os.urandom(1)[0] & 1
        self.block_size = 8
        self.input_size = 2 * self.block_size
        self.RO1 = PRF(self.block_size)
        self.RO2 = PRF(self.input_size)

    def function1(self, M):
        L, R = M[:self.block_size], M[self.block_size:]
        L, R = R, xor(L, self.RO1.tran(R))
        L, R = R, xor(L, self.RO1.tran(R))
        return L+R

    def function2(self, M):
        return self.RO2.tran(M)

    def roll(self, M, inverse):
        assert inverse == False, "In Challenge2, inverse is not allowed"
        return [self.function1,self.function2][self.coin](M)

class Challenge3:
    def __init__(self):
        self.coin = os.urandom(1)[0] & 1
        self.block_size = 8
        self.input_size = 2 * self.block_size
        self.RO1 = PRF(self.block_size)
        self.RO2 = PRF(self.input_size)

    def function1(self, M, inverse):
        if not inverse:
            L, R = M[:self.block_size], M[self.block_size:]
            L, R = R, xor(L, self.RO1.tran(R))
            L, R = R, xor(L, self.RO1.tran(R))
            L, R = R, xor(L, self.RO1.tran(R))
        else:
            L, R = M[:self.block_size], M[self.block_size:]
            L, R = xor(R, self.RO1.tran(L)), L
            L, R = xor(R, self.RO1.tran(L)), L
            L, R = xor(R, self.RO1.tran(L)), L
        return L+R

    def function2(self, M, inverse):
        if inverse or not inverse:        
            return self.RO2.tran(M)

    def roll(self, M, inverse):
        return [self.function1,self.function2][self.coin](M,inverse)

class Challenge4:
    def __init__(self):
        self.coin = os.urandom(1)[0] & 1
        self.block_size = 8
        self.input_size = 2 * self.block_size
        self.PRP1 = PRP(self.block_size)
        self.PRP2 = PRP(self.input_size)

    def function1(self, M, inverse):
        X, T = M[:self.block_size], M[self.block_size:]
        X = xor(X, T)
        for _ in range(2):
            X = xor(self.PRP1.tran(X, inverse),T)
        return X

    def function2(self, M, inverse):
        return self.PRP2.tran(M, inverse)[:self.block_size]

    def roll(self, M, inverse):
        return [self.function1,self.function2][self.coin](M,inverse)

class Challenge5:
    def __init__(self):
        self.coin = os.urandom(1)[0] & 1
        self.block_size = 1
        self.input_size = self.block_size
        self.PRP = PRP(self.block_size)
        self.PRF = PRF(self.input_size)

    def function1(self, M):
        return xor(bytes(1),self.PRP.tran(M))

    def function2(self, M):
        return xor(self.PRF.tran(M),bytes(1))

    def roll(self, M, inverse):
        assert inverse == False, "In Challenge 5, inverse is not allowed"
        return [self.function1,self.function2][self.coin](M)

题目代码挺长的，先简要地描述一下主要任务：

• 题目连续生成五个猜硬币挑战，通过一个挑战才能进行下一个挑战
• 对于每个挑战，需要猜测成功33次硬币即可通过挑战
• 猜测硬币的依据是：靶机提供输入功能可以输入一段字节流，而对于硬币为0或为1，会有不同的随机数产生方式，对输入的字节流产生随机数并返回。
• 对于每个挑战中的每一次猜硬币，可以指定输入次数，这个次数是五次挑战共享的，也就是说，如果前面用的次数多，后面能用的次数就少；前面用的少，后面能用的次数就很充裕。
• 对于指定的challenge，可以使用inverse功能，获取某个输入的解密结果

那么核心任务就是：

• 判断出每个challenge中，硬币为0或1时产生的随机数有什么不同，从而构造对应的输入，用得到的对应输出的特点去判断
• 对每一次挑战，尽可能用更少的输入次数，从而使后面的次数更加充裕

然后，对于5个challenge，其随机数产生都是基于两个类的：

class PRP():
    def __init__(self, n):
        self.domain_cache = {}
        self.range_cache = {}
        self.n = n

    def tran(self, m, inverse = False):
        if not inverse:
            x = m
            if x in self.domain_cache:
                return self.domain_cache[x]
            while True:
                y = os.urandom(self.n)
                if y in self.range_cache:continue
                self.domain_cache[x] = y
                self.range_cache[y] = x    
                return y
        else:
            y = m
            if y in self.range_cache:
                return self.range_cache[y]
            while True:
                x = os.urandom(self.n)
                if x in self.domain_cache:continue
                self.domain_cache[x] = y
                self.range_cache[y] = x    
                return x

class PRF():
    def __init__(self, n):
        self.domain_cache = {}
        self.range_cache = {}
        self.n = n 

    def tran(self, x):
        if x not in self.domain_cache:
            self.domain_cache[x] = os.urandom(self.n)
        return self.domain_cache[x]

这两个类分别指的是伪随机置换(PRP)和伪随机函数(PRF)，其具体区别可以参考：

【密码学】PRP和PRF_prf算法-CSDN博客

那么接下来就逐个挑战分析：

challenge 1

class Challenge1:
    def __init__(self):
        self.coin = os.urandom(1)[0] & 1
        self.block_size = 8
        self.input_size = 2 * self.block_size
        self.RO1 = PRF(self.block_size)
        self.RO2 = PRF(self.input_size)

    def function1(self, M):
        L, R = M[:self.block_size], M[self.block_size:]
        L, R = R, xor(L, self.RO1.tran(R))
        return L+R

    def function2(self, M):
        return self.RO2.tran(M)

    def roll(self, M, inverse):
        assert inverse == False, "In Challenge1, inverse is not allowed"
        return [self.function1,self.function2][self.coin](M)

可以看到，对于硬币为0或为1，其对输入的串的处理方式不同：

• 为0，把输入串分为左右两部分，然后如下得到结果

L, R = R, xor(L, self.RO1.tran(R))

• 为1，直接输出一个长度为16的随机字节流

那么如何区分也很显然。我们请求一次输入次数，然后输入长度为16的全0字节，然后若靶机返回的输出前8个字节为全0，说明硬币为0；否则为1。

challenge 2

class Challenge2:
    def __init__(self):
        self.coin = os.urandom(1)[0] & 1
        self.block_size = 8
        self.input_size = 2 * self.block_size
        self.RO1 = PRF(self.block_size)
        self.RO2 = PRF(self.input_size)

    def function1(self, M):
        L, R = M[:self.block_size], M[self.block_size:]
        L, R = R, xor(L, self.RO1.tran(R))
        L, R = R, xor(L, self.RO1.tran(R))
        return L+R

    def function2(self, M):
        return self.RO2.tran(M)

    def roll(self, M, inverse):
        assert inverse == False, "In Challenge2, inverse is not allowed"
        return [self.function1,self.function2][self.coin](M)

与challenge1的区别在于，硬币为0时，这个类feistel结构多进行了一轮，因此无法直接从输出进行判断。

但是解决方式也很容易，我们请求两次输入次数：

如果硬币是0：

• 第一次，输入长度为16的全0字节流，得到对应输出，推导一下可以知道输出的左右两部分是如下形式：

$$t(0),t(t(0))$$

• 第二次，我们输入：

$$t(0),0$$

• 可以简单推导一下，我们得到的输出应该是：

$$0,t(0)$$

而如果硬币是1，显然输出不会是这个结构，因此我们就可以通过挑战二。

challenge 3

class Challenge3:
    def __init__(self):
        self.coin = os.urandom(1)[0] & 1
        self.block_size = 8
        self.input_size = 2 * self.block_size
        self.RO1 = PRF(self.block_size)
        self.RO2 = PRF(self.input_size)

    def function1(self, M, inverse):
        if not inverse:
            L, R = M[:self.block_size], M[self.block_size:]
            L, R = R, xor(L, self.RO1.tran(R))
            L, R = R, xor(L, self.RO1.tran(R))
            L, R = R, xor(L, self.RO1.tran(R))
        else:
            L, R = M[:self.block_size], M[self.block_size:]
            L, R = xor(R, self.RO1.tran(L)), L
            L, R = xor(R, self.RO1.tran(L)), L
            L, R = xor(R, self.RO1.tran(L)), L
        return L+R

    def function2(self, M, inverse):
        if inverse or not inverse:        
            return self.RO2.tran(M)

    def roll(self, M, inverse):
        return [self.function1,self.function2][self.coin](M,inverse)

相比起challenge2，又多加了一轮feistel，不过不同的是，我们可以通过inverse进行解密。

那就很简单了，我们请求两次输入次数，第一次随便输入一个字节流并获得其加密结果，第二轮输入得到的加密结果，并看inverse的结果与第一轮是否相等就好了。相等为0，否则为1。

challenge 4

class Challenge4:
    def __init__(self):
        self.coin = os.urandom(1)[0] & 1
        self.block_size = 8
        self.input_size = 2 * self.block_size
        self.PRP1 = PRP(self.block_size)
        self.PRP2 = PRP(self.input_size)

    def function1(self, M, inverse):
        X, T = M[:self.block_size], M[self.block_size:]
        X = xor(X, T)
        for _ in range(2):
            X = xor(self.PRP1.tran(X, inverse),T)
        return X

    def function2(self, M, inverse):
        return self.PRP2.tran(M, inverse)[:self.block_size]

    def roll(self, M, inverse):
        return [self.function1,self.function2][self.coin](M,inverse)

挑战4中，如果硬币为0，则会将输入分为左右两部分，并反复进行tran和异或操作。不过可以看出，如果我们将输入的右半部分取为全0，异或操作相当于没有进行，而只有两轮tran。

那么同样，我们请求两次输入，第一次输入长度为16的全0字节流得到加密结果，然后第二次将加密结果再连接上8字节的0去inverse，解密得到全0说明硬币为0，否则为1。

challenge 5

class Challenge5:
    def __init__(self):
        self.coin = os.urandom(1)[0] & 1
        self.block_size = 1
        self.input_size = self.block_size
        self.PRP = PRP(self.block_size)
        self.PRF = PRF(self.input_size)

    def function1(self, M):
        return xor(bytes(1),self.PRP.tran(M))

    def function2(self, M):
        return xor(self.PRF.tran(M),bytes(1))

    def roll(self, M, inverse):
        assert inverse == False, "In Challenge 5, inverse is not allowed"
        return [self.function1,self.function2][self.coin](M)

这题与前面的4个challenge有两个明显区别：

• 加密的明文仅有1字节
• 既有PRP又有PRF

那么肯定就是要利用两者的区别。而最明显的区别就在于，PRP会建立一个双射，从而保证能进行逆操作，但是PRF不会。

什么意思呢？比如我们输入1和2，PRP能保证输入的两个自变量对应的函数值不同，但是PRF不保证，也就是说输入1，2，返回值可能均为1。

而我们前面共请求了1+2+2+2次，还可以用48次。因此可以请求48次输入次数，并用靶机返回的值建立字典并检查字典长度。如果长度为48则硬币大概率为0，否则为1。

注意我这里说的是大概率为0，概率具体有多大呢？我们其实可以把他看做一个等价的事件，也就是：

• 从0-255中随机抽取48次，48次全部都不一样。

这个时候我们的判断就会失败，因为此时PRF和PRP字典长度均为48。而这个失败的概率为：

$$\frac{256}{256}*\frac{255}{256}*\frac{254}{256}*...\frac{209}{256}$$

而经计算，这个概率大约为：

t = 0.009029416209217144

可以看到对于每一次，我们只有不到1%的非常小的概率失败，而我们同样也可以计算33次全部成功的概率如下：

$$P = (1-t)^{33}$$

计算得到：

0.7413190801200953

所以我们有很大概率成功，这也是生日攻击的理论基础。

完整exp如下：

from pwn import *
from tqdm import *

#context.log_level = 'debug'
r = remote("node4.buuoj.cn",27756)

#Easy
#challenge1
r.recvuntil(b"solving 1? > ")
r.sendline(b"1")
for i in trange(33):
    r.recvuntil(b"msg? >")
    r.sendline(b"0" * 32)
    r.recvuntil(b"inverse? >")
    r.sendline(b"n")
    temp = r.recvline().strip().decode()
    if("0000000000000000" in temp):
        r.sendline(b"0")
    else:
        r.sendline(b"1")

#challenge2
r.recvuntil(b"solving 2? > ")
r.sendline(b"2")
for i in trange(33):
    temp = [0,0]
    #first
    r.recvuntil(b"msg? >")
    r.sendline(b"0" * 32)
    r.recvuntil(b"inverse? >")
    r.sendline(b"n")
    temp[0] = r.recvline().strip().decode()
    #second
    r.recvuntil(b"msg? >")
    r.sendline((temp[0][:16]+"0"*16).encode())
    r.recvuntil(b"inverse? >")
    r.sendline(b"n")
    temp[1] = r.recvline().strip().decode()
    if(temp[1][:16] == "0000000000000000"):
        r.sendline(b"0")
    else:
        r.sendline(b"1")


#challenge3
r.recvuntil(b"solving 3? > ")
r.sendline(b"2")
for i in trange(33):
    temp = [0,0,0]
    #first
    r.recvuntil(b"msg? >")
    r.sendline(b"0" * 32)
    r.recvuntil(b"inverse? >")
    r.sendline(b"n")
    temp[0] = r.recvline().strip().decode()
    #second
    r.recvuntil(b"msg? >")
    r.sendline(temp[0].encode())
    r.recvuntil(b"inverse? >")
    r.sendline(b"y")
    temp[1] = r.recvline().strip().decode()
    #third
    if(temp[1][:16] == "0000000000000000"):
        r.sendline(b"0")
    else:
        r.sendline(b"1")
print(r.recvline())
#flag{7b106778-5048-4d9d-bd30-84cfc7d5b48e}


#Hard
#challenge4
r.recvuntil(b"solving 4? > ")
r.sendline(b"2")
for i in trange(33):
    temp = [0,0]
    #first
    r.recvuntil(b"msg? >")
    r.sendline(b"0" * 32)
    r.recvuntil(b"inverse? >")
    r.sendline(b"n")
    temp[0] = r.recvline().strip().decode()
    #second
    r.recvuntil(b"msg? >")
    r.sendline((temp[0]+"0"*16).encode())
    r.recvuntil(b"inverse? >")
    r.sendline(b"y")
    temp[1] = r.recvline().strip().decode()
    #third
    if(temp[1] == "0000000000000000"):
        r.sendline(b"0")
    else:
        r.sendline(b"1")

#challenge5
r.recvuntil(b"solving 5? > ")
r.sendline(b"48")
for i in trange(33):
    dic = {}
    for j in range(48):
        r.recvuntil(b"msg? >")
        r.sendline((hex(j)[2:].zfill(2).encode()))
        r.recvuntil(b"inverse? >")
        r.sendline(b"n")
        temp = r.recvline().strip().decode()
        dic[temp] = j
    if(len(dic) == 48):
        r.sendline(b"0")
    else:
        r.sendline(b"1")
print(r.recvline())

#flag{u_4re_Prf&Pr9_M4st3r!#28a3gg31_82jf124d3_3842sa16ds29}