糖醋小鸡块的blog
0%

2024-BeginCTF-wp-crypto

发表于 更新于 分类于 Valine：

打这个比赛把之前香山杯带的帐——rescue prime的CICO问题的论文看了一遍，然后解题过程中发现自己完全不了解的的东西真的还有很多很多。

*代表赛中未做出的题目。

PAD

题目描述：

1
某同学在学习RSA得时候，觉得仅仅靠着比特位得RSA是不安全的，于是参考了部分资料后，灵光乍现

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import random, math

from Crypto.Util.number import *
from flag import flag
flag=flag[:64]
assert len(flag) == 64

class RSA():
    def __init__(self, m: int):
        self.p, self.q, self.e, self.m = getPrime(512), getPrime(512), getRandomRange(1,8), m
        self.n = self.p * self.q
    def Publickey(self):
        return (self.n, self.e,self.c)
    def Encrypt(self):
        pad = PAD(m=self.m, e=0)
        pad.PAD()
        self.c = (pad.e,pow(pad.M, self.e, self.n))
class PAD():
    def __init__(self, m: int, e):
        self.e, self.m, self.mbits = e, m, m.bit_length()
        if e == 0:
            self.e = getRandomRange(2, 7)
    def PAD(self):
        self.M = pow(self.e, self.mbits) + pow(self.m, self.e)
GIFT = bytes_to_long(flag)
with open("GIFT.txt", "w") as f:
    for i in range(40):
        rsa = RSA(m=GIFT)
        rsa.Encrypt()
        f.write(str(rsa.Publickey()) + "\n")

以及一个比较长的文本文件GIFT.txt，在这里就不放出了(之后的PAD_revenge同理)。

题目主要流程，就是给出了40组如下形式的加密数据：

其中e1为1-8的数，e2为2-7的数，并且每一组的n都不同。给出每一组数据的e1、e2、n、c，要求还原flag。

最直观的想法就是找最好算的数据，比如在GIFT里真的可以找到一组e1为1、e2为2的数据，那么也就有：

而m是511bit的量(begin打头)，所以可以直接作差后开平方得到。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from Crypto.Util.number import *
from gmpy2 import *

with open(r"py\crypto\2024\BeginCTF 2024\pad_output.txt","r") as f:
    for i in range(40):
        temp = eval(f.readline())
        if(temp[1] == 1 and temp[2][0] == 2):
            n = temp[0]
            e1 = temp[1]
            e2 = temp[2][0]
            c = temp[2][1]

c = c - 2**511
m = iroot(c,2)[0]
print(long_to_bytes(m))

#begin{8E6C79D2-E960-C57A-F3E4-A52BC827ED6B_Dragon_Year_happy!!!}



fake_n

题目描述：

1
来道rsa吧！咦？这n怎么是假的？

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from Crypto.Util.number import *
from secret import flag

def fakeN_list():
    puzzle_list = []

    for i in range(15):
        r = getPrime(32)
        puzzle_list.append(r)

    p = getPrime(32)
    q = getPrime(32)
    com = p*q

    puzzle_list.append(com)

    return puzzle_list

def encrypt(m,e,fake_n_list):

    fake_n = 1
    for i in range(len(fake_n_list)):
        fake_n *= fake_n_list[i]

    really_n = 1
    for i in range(len(fake_n_list)-1):
        really_n *= fake_n_list[i]

    c = pow(m,e,really_n)

    print("c =",c)
    print("fake_n =",fake_n)

if __name__ == '__main__':
    m = bytes_to_long(flag)
    e = 65537
    fake_n_list = fakeN_list()
    encrypt(m,e,fake_n_list)

'''
c = 6451324417011540096371899193595274967584961629958072589442231753539333785715373417620914700292158431998640787575661170945478654203892533418902
fake_n = 178981104694777551556050210788105224912858808489844293395656882292972328450647023459180992923023126555636398409062602947287270007964052060975137318172446309766581
'''

总而言之这题生成了17个32bit的素数，并选用其中15个作为RSA加密的模数，但是不告诉我们到底选了哪15个。

而32bit的素数都是易分解的，所以只要获取完整分解后爆破所有可能的15个素数的组合就总有一个是正确的模数，解密成功用是否是begin开头就行。不过我这边比较偷懒，想着说不定flag比较短，所以直接多次shuffle掉素数列表，并取前面十个的积作模数，很容易就能跑出来一次解密成功。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from Crypto.Util.number import *
from factordb.factordb import FactorDB
from random import *

c = 6451324417011540096371899193595274967584961629958072589442231753539333785715373417620914700292158431998640787575661170945478654203892533418902
fake_n = 178981104694777551556050210788105224912858808489844293395656882292972328450647023459180992923023126555636398409062602947287270007964052060975137318172446309766581

f = FactorDB(fake_n)
f.get_factor_list()
f.connect()
primeslist = f.get_factor_list()

for j in range(100):
    shuffle(primeslist)

    phi = 1
    n = 1
    for i in primeslist[:10]:
        phi *= (i-1)
        n *= i

    d = inverse(65537,phi)
    print(long_to_bytes(pow(c,d,n)))

#begin{y0u_f1nd_th3_re4l_n}



baby_classic

题目描述：

1
你这辈子就是被古典密码给害了，后面我忘了

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
from random import *
from string import *
import numpy as np
from secret import plaintext

ls = ascii_uppercase + '_.*'

def generate_str(length):
    s = ""
    for i in range(length):
        s += choice(ls)
    return s

def str2mat(s):
    res = np.zeros((len(s) // 6, 6),dtype=int)
    for i in range(0,len(s)):
        res[i // 6, i % 6] = ls.index(s[i])
    return res

def mat2str(mat):
    s = ""
    for i in range(len(mat) * 6):
        s += ls[mat[i // 6, i % 6]]
    return s

def encrypt(plaintext,key1,key2):
    mat_plaintext = str2mat(plaintext)
    mat_key1 = str2mat(key1)
    mat_key2 = str2mat(key2)

    enc_matrix = np.dot(mat_plaintext,mat_key1) % 29
    for i in range(len(enc_matrix)):
        for j in range(len(enc_matrix[i])):
            enc_matrix[i][j] = (enc_matrix[i][j] + mat_key2[0][j]) % 29

    return mat2str(enc_matrix)

if __name__ == "__main__":

    assert len(plaintext) == 72
    m = generate_str(48)
    key1 = generate_str(36)
    key2 = generate_str(6)
    c = encrypt(m, key1, key2)
    ciphertext = encrypt(plaintext, key1, key2)

    '''
    flag = "begin{" + hashlib.md5(plaintext.encode()).hexdigest() + "}"
    '''

    print(f"m = {m}")
    print(f"c = {c}")
    print(f"ciphertext = {ciphertext}")


'''
output:
m = VOWAS*TED.AE_UMLVFV*W*HSSSTZIZZZDAKCLXZKM_E*VR*Y
c = QLOKQGUWMUTGZSDINCQVIVOLISFB_FC.IC_OSPLOBGOVSCZY
ciphertext = MHDTBJSZXLHH.Z.VWGLXUV.SDQUPAMEPNVQVQZX_CBDZHM_IBZRGLJP_YSBDXN.VACLDGCO_
'''

题目的加密过程梳理下来其实就是：

其中，未知的量分别是K1、K2。K1是密钥矩阵1，是一个6x6的矩阵，每个元素都是模29下的随机数。K2是密钥矩阵2，但每一行均相同。

题目任务就是给出了一组长度为48的已知的明密文对m、c，并且给出长度为72的ciphertext，要求我们解出ciphertext对应的明文，并且md5处理后就是flag。

那么主要问题就是由已知的明密文对m、c求解出密钥矩阵K1和K2。而由于长度是48所以其对应的矩阵方程就是：

比较自然的思路是，由于K2的每一行都相同，所以其实最多需要爆破6个0-28的数字就一定有一个正确的K2矩阵，然后判断K2是否正确的依据，就是如下矩阵方程是否有解：

这样已经足够做出题目了，因为29^6确实也不算特别大。

方法一

不过其实有更好的做法。注意到其实对于明文来说，他每六个字符的加密都是独立的，所以我们可以把上面的矩阵方程拆分成8个如下形式的矩阵方程：

而这样做的好处是，我们任取其中两个矩阵方程(下面就不写矩阵大小了)：

然后作差就得到：

这样就可以把K2消掉。而八组数据最多可以作出七组线性无关的差，就可以重新再组合成一个矩阵方程。而对于K1来说，只需要六组数据就可以达到满秩，因此完全足够了。

解出K1后代入任意一组就可以解出K2，然后就可以求出ciphertext对应的明文。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
from string import *
import hashlib

ls = ascii_uppercase + '_.*'

m = "VOWAS*TED.AE_UMLVFV*W*HSSSTZIZZZDAKCLXZKM_E*VR*Y"
c = "QLOKQGUWMUTGZSDINCQVIVOLISFB_FC.IC_OSPLOBGOVSCZY"
ciphertext = "MHDTBJSZXLHH.Z.VWGLXUV.SDQUPAMEPNVQVQZX_CBDZHM_IBZRGLJP_YSBDXN.VACLDGCO_"

dic = {}
for i in range(len(ls)):
    dic[ls[i]] = i

m = [dic[char] for char in m]
c = [dic[char] for char in c]
ciphertext = [dic[char] for char in ciphertext]

M = []
C = []
delta_M = []
delta_C = []
for i in range(0,48,6):
    M.append([m[j] for j in range(i,i + 6)])
    C.append([c[j] for j in range(i,i + 6)])
for i in range(0,42,6):
    delta_M.append([(m[j] - m[j+6])%29 for j in range(i,i + 6)])
    delta_C.append([(c[j] - c[j+6])%29 for j in range(i,i + 6)])

M_mat = Matrix(Zmod(29),M)
C_mat = Matrix(Zmod(29),C)
delta_M_mat = Matrix(Zmod(29),delta_M)
delta_C_mat = Matrix(Zmod(29),delta_C)
key1_mat = delta_M_mat.solve_right(delta_C_mat)
key2_mat = C_mat - M_mat*key1_mat
key2_vector = vector(Zmod(29),key2_mat[0])

Cipher = []
for i in range(0,72,6):
    Cipher.append([ciphertext[j] for j in range(i,i + 6)])
Cipher_mat = Matrix(Zmod(29),Cipher)
Plain_mat = (Cipher_mat - Matrix(Zmod(29),[key2_vector for i in range(72//6)]))*key1_mat.inverse()

plaintext = ""
for i in Plain_mat:
    for j in i:
        plaintext += ls[j]
print(plaintext)

#YOU_KNOW_THE_MYSTERY_OF_THE_MATRIX**BUT_THIS_IS_BEGINNING_OF_CRYPTOLOGY.

flag = "begin{" + hashlib.md5(plaintext.encode()).hexdigest() + "}"
print(flag)

#begin{d70c49eebc8158985f33a5eb3caa5733}

方法二

赛后在群里看到另一种比较巧妙的做法。这里是要利用K2矩阵每一行都相同的这一特点，然后就可以把刚才的矩阵方程：

直接看作是一个完整的矩阵乘法：

这个意思就是把M最后加一列1，然后把K2的行加到K1矩阵尾部，形成两个新的矩阵。然后就可以直接解这个矩阵方程，直接得到K1、K2了。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
from string import *
import hashlib

ls = ascii_uppercase + '_.*'

m = "VOWAS*TED.AE_UMLVFV*W*HSSSTZIZZZDAKCLXZKM_E*VR*Y"
c = "QLOKQGUWMUTGZSDINCQVIVOLISFB_FC.IC_OSPLOBGOVSCZY"
ciphertext = "MHDTBJSZXLHH.Z.VWGLXUV.SDQUPAMEPNVQVQZX_CBDZHM_IBZRGLJP_YSBDXN.VACLDGCO_"

dic = {}
for i in range(len(ls)):
    dic[ls[i]] = i

m = [dic[char] for char in m]
c = [dic[char] for char in c]
ciphertext = [dic[char] for char in ciphertext]

M = []
C = []
delta_M = []
delta_C = []
for i in range(0,48,6):
    M.append([m[j] for j in range(i,i + 6)]+[1])
    C.append([c[j] for j in range(i,i + 6)])

M_mat = Matrix(Zmod(29),M)
C_mat = Matrix(Zmod(29),C)
key1_mat = M_mat.solve_right(C_mat)[:-1]
key2_vec = M_mat.solve_right(C_mat)[-1:]
key2_mat = Matrix(Zmod(29),list(key2_vec)*12)

Cipher = []
for i in range(0,72,6):
    Cipher.append([ciphertext[j] for j in range(i,i + 6)])
Cipher_mat = Matrix(Zmod(29),Cipher)
Plain_mat = (Cipher_mat-key2_mat)*key1_mat.inverse()

plaintext = ""
for i in Plain_mat:
    for j in i:
        plaintext += ls[j]
print(plaintext)

#YOU_KNOW_THE_MYSTERY_OF_THE_MATRIX**BUT_THIS_IS_BEGINNING_OF_CRYPTOLOGY.

flag = "begin{" + hashlib.md5(plaintext.encode()).hexdigest() + "}"
print(flag)

#begin{d70c49eebc8158985f33a5eb3caa5733}



Hard_ECC

题目描述：

1
baby不是真baby的话，那hard当然也不是真hard的啦

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from flag import flag

A = [0,
     3,
     0,
     973467756888603754244984534697613606855346504624,
     864199516181393560796053875706729531134503137794]
p = 992366950031561379255380016673152446250935173367
ec = EllipticCurve(GF(p), [A[0], A[1], A[2], A[3], A[4]])
T = ec.random_point()
secret = int.from_bytes(flag, 'little')
Q = T * secret
print(T, Q)
# (295622334572794306408950267006569138184895225554 : 739097242015870070426694048559637981600496920065 : 1)
# (282367703408904350779510132139045982196580800466 : 411950462764902930006129702137150443195710071159 : 1)

模数一看就很小，阶也确实不大。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from Crypto.Util.number import *

A = [0,
     3,
     0,
     973467756888603754244984534697613606855346504624,
     864199516181393560796053875706729531134503137794]
p = 992366950031561379255380016673152446250935173367
E = EllipticCurve(GF(p), [A[0], A[1], A[2], A[3], A[4]])

T = (295622334572794306408950267006569138184895225554 , 739097242015870070426694048559637981600496920065)
Q = (282367703408904350779510132139045982196580800466 , 411950462764902930006129702137150443195710071159)
T = E(T)
Q = E(Q)

secret = T.discrete_log(Q)
print(long_to_bytes(int(secret))[::-1])

#begin{it_is_hard?}



OEIS2

题目描述：

1
听说可以查表？

题目：

1
2
3
4
5
6
from hashlib import *
upper = 2**28 + 5
res = 1
for i in range(1, upper + 1):
    res *= i
flag = 'Beginctf{' + sha256(str(sum([int(i) for i in str(res)])).encode()).hexdigest() + '}'

强网杯speed up的强化版，这次是要算2^28+5的阶乘的各位数字之和。

显然这个应该查不了OEIS，所以只有sage或者mathematica爆算，我是没有下mathematica所以选择了sage，并且担心虚拟机内存分配的不太够所以选择用本机的sage9.3跑，虽然需要半小时左右但是的确可以出。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from hashlib import *

if(0):
    number = factorial(2**28+5)

    t = sum(int(d) for d in str(number))
    print(t)

#9355117392
t = 9355117392
flag = 'Beginctf{' + sha256(str(t).encode()).hexdigest() + '}'
print(flag)

#Beginctf{c60a2e5c9e9572ed848776f282a9c90d6ca0fe29f8308b0b9b43c61d493133e9}



PAD_revenge

题目描述：

1
M=C?

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

from Crypto.Util.number import *
from flag import flag

assert len(flag) == 64

class RSA():
    def __init__(self, m: int):
        self.p, self.q, self.e, self.m = getPrime(256), getPrime(256), getRandomRange(1,9), m
        self.n = self.p * self.q
    def Publickey(self):
        return (self.n, self.e,self.c)
    def Encrypt(self):
        pad = PAD(m=self.m, e=0)
        pad.PAD()
        self.c = (pad.e,pow(pad.M, self.e, self.n))
class PAD():
    def __init__(self, m: int, e):
        self.e, self.m, self.mbits = e, m, m.bit_length()
        if e == 0:
            self.e = getRandomRange(1, 9)
    def PAD(self):
        self.M = pow(self.e, self.mbits) + pow(self.m, self.e)
GIFT = bytes_to_long(flag)

with open("GIFT.txt", "w") as f:
    for i in range(100):
        rsa = RSA(m=GIFT)
        rsa.Encrypt()
        data=rsa.Publickey()
        if data[1]*data[2][0]<=2:
            continue
        f.write(str(data) + "\n")

和前面的PAD区别不大，只是这次限制了e1和e2相乘必须大于2，否则就不给出这组数据。并且这个题目给出了最多100组。

不过只限制了相乘大于2，那完全可以找几组等于3的嘛。所以就能找到几组符合要求的等式：

crt起来过后直接开三次根就行了。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import *
from gmpy2 import *
from sympy.ntheory.modular import crt
#M = crt(n,c)[0]

n = []
c = []
with open(r"py\crypto\2024\BeginCTF 2024\pad_revenge_output.txt","r") as f:
    for i in range(97):
        temp = eval(f.readline())
        if(temp[1] == 1 and temp[2][0] == 3):
            n.append(temp[0])
            c.append(temp[2][1]-3**511)

M = crt(n,c)[0]
print(long_to_bytes(iroot(M,3)[0]))

#begin{There_wonot_be_any_surprises_this_time230E03984617EEEEE13}

出题人预期应该是求一个一元模方程组的解，就是把所有方程凑成同阶之后crt+copper，那样可以把所有数据都用上。不过其实就正常思维来说，没有人会想用指数比较大的数据，所以没必要。



baph

题目描述：

1
签到题1.0（flag格式为flag{}）

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from base64 import b64encode
from Crypto.Util.number import *
from string import ascii_letters
from secrets import flag

ls = ascii_letters + '!,.? {}' + '01232456789'
assert all([i in ls for i in flag])
ba = b64encode(flag.encode())
baph, key = '', ''

for b in ba.decode():
	if b.islower():
		baph += b.upper()
		key += '0'
	else:
		baph += b.lower()
		key += '1'

baph = baph.encode()
key = long_to_bytes(int(key, 2))
enc = b''
for i in range(len(baph)):
	enc += long_to_bytes(baph[i] ^ key[i % len(key)])
f = open('flag.enc', 'wb')
f.write(enc)
f.close()

以及一个flag.enc文件，我这里就直接给出他的字节流：

1
b'\xf7.\x1cf\x94\\\x11\x82\x8c\x1c\x9ba\xce."\x1e\xaa\x18\x1d\xae\x8aI\xe2y\xcf-)f\x87\x1c \xa1\xbb\x1c\x97{\xf7\x1b6~\xac\x183\xbc\xa7I\xd8\x1b\xce\x04\x1cx\xad]\t\xd4\xb4]\xccg\xc9\x0b6f\x97]\x11\xbc\xa7I\xc0g\xcf*&g\x94\x1c\'\xaa\xb4c\xd4c\xf4P6~\xaa"0\xae\xa7]\xc8\x16'

主要流程是：

  • 把flag进行base64编码，得到ba
  • 初始化空的key
  • 遍历ba中的字符，如果是小写字母，则转成大写，并且key加上一个”0”；否则将字符转成小写，key加上”1”
  • 遍历完成后，得到一个大小写转换后的ba，记为baph；以及一个比特长度和baph相等的key
  • 将key转为二进制后，逐个与baph作异或得到密文enc

那么观察enc的长度发现是96，也就是说key也就是96bit，就是12个字节。而对于已知的flag头flag{以及知道的flag尾部，可以再爆破三个字符，得到一个完整的九字节，base64编码后就刚好是12个字符，也就刚好等于key的长度。那么判断解密出来的是不是都在base64编码表里，就可以确定是不是可能的正确key了。

然后对所有可能的正确key反解出baph，再大小写转换后得到ba，看base64解码后是不是全在ls里就可以。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
from Crypto.Util.number import *
from gmpy2 import *
from pwn import xor
from base64 import *
from string import *
from tqdm import *

with open(r"D:\题\2024\BeginCTF 2024\baph\题目附件\flag.enc","rb") as f:
    enc = f.read()

ls = ascii_letters + '!,.? {}' + '0123456789'
table = ascii_letters + digits + "+/="

def dec(c):
    baph = b""
    for char in c.decode():
        if char.islower():
            baph += char.upper().encode()
        else:
            baph += char.lower().encode()
    try:
        m = b64decode(baph).decode()
        if(all(i in ls for i in m)):
            return m
        else:
            return None
    except:
        return None

for t1 in tqdm(ls):
    for t2 in ls:
        for t3 in ls:
            prefix = b64encode(("flag{"+t1+t2+t3+"}").encode()).decode()
            baph = b""
            for b in prefix:
                if b.islower():
                    baph += b.upper().encode()
                else:
                    baph += b.lower().encode()
                    
            key = xor(baph,enc[:8]+enc[-4:])

            m = b""
            for i in range(len(enc)):
                m += long_to_bytes(enc[i] ^ key[i % len(key)])

            if(all(chr(i) in table for i in m)):
                flag = dec(m)
                if(flag != None):
                    print(flag)

#flag{Congratulations!!! Sometimes explosive attacks can be effective!!!}



我玩青水的

题目描述：

1
开局霸体螺旋丸起手，替身反手飞雷神，我们青水玩家实在是太有操作啦！所以为什么不能用玩青水的大脑做这题呢？

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
e = 2
p = getPrime(512)
c = pow(m, e, p)

print(f"p = {p}")
print(f"c = {c}")

'''
p = 7709388356791362098686964537734555579863438117190798798028727762878684782880904322549856912344789781854618283939002621383390230228555920884200579836394161
c = 5573755468949553624452023926839820294500672937008992680281196534187840615851844091682946567434189657243627735469507175898662317628420037437385814152733456
'''

求个二次剩余就可以了，不过我反正统一有限域开根。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
from Crypto.Util.number import *

e = 2
p = 7709388356791362098686964537734555579863438117190798798028727762878684782880904322549856912344789781854618283939002621383390230228555920884200579836394161
c = 5573755468949553624452023926839820294500672937008992680281196534187840615851844091682946567434189657243627735469507175898662317628420037437385814152733456

PR.<x> = PolynomialRing(Zmod(p))
f = x^e - c
res = f.roots()
for i in res:
    print(long_to_bytes(int(i[0])))

#begin{quadr4ticresidue_i5_s0_3asy}



begin_rsa

题目描述：

1
也许，这只是开始呢

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.number import *
from gmpy2 import *
from secret import flag
m = bytes_to_long(flag)

while True:
    e = 65537
    p1 = getPrime(512)
    q1 = getPrime(512)
    n1 = p1 * q1
    p1_xor_q1_low = (p1 ^ q1) & ((1 << 402) - 1)
    if p1_xor_q1_low >= 10**121 and p1_xor_q1_low <= 10**122 - 1:
        p2 = next_prime(p1_xor_q1_low)
        q2 = int(str(p2)[61:] + str(p2)[:61])
        n2 = p2 * q2
        if isPrime(p2) and isPrime(q2):
            delta = p2 - p1_xor_q1_low
            c = pow(m, e, n1)
            print(f"delta = {delta}")
            print(f"n1 = {n1}")
            print(f"n2 = {n2}")
            print(f"c = {c}")
            break

'''
delta = 61
n1 = 150838784531830142890659431841610000561921043629625618437510373123377520444955469509903631548754842609295975005302780725591929018884805452687677684641162979092069629817740554095750189248769936750051172301891394503776919559958638203717583333429953061416588208428893436430392654983424277005324307321992921302331
n2 = 102603788692700558034198259394482879736866145355211103067657972779629890324418113112441175321034955422723378003769267804892308121194871227786783930178021669484220789624643889449429959522560822967157677629720685465873700893389751397027159036419
c = 100199300622156732994823007073822662584719346985430234367094043002848132740563819931486477742264272832060136969084318984512567787814048659200236334994498141562184235841854521058494238451300610422156322926341430748222140189349893444976932184031798101999886029853099171189139509539715437105818418407563733036131
'''

题目先生成两个素数p1、q1，然后计算他们异或的低402位记为p1_xor_q1_low，同时确保这个值是122个十进制数字。

之后，取这个值的nextprime作为p2，并且将p2的十进制前半截和后半截交换了一下得到q2。确保q2也是素数后，给出p1、q1的乘积n1以及p2、q2的乘积n2，并给出用n1加密flag的密文c，要求还原flag。

那么顺序肯定是先求p2、q2得到p1_xor_q1_low，再求p1、q1。而对于求p2、q2来说，突破点在于q2是p2的十进制前后半截交换的结果。也就是说p2、q2可以分别写成：

那么n2也就是：

展开也就是：

那可以看出，n2的十进制低61位就是ab的低61位，高61位就是ab的高61位，但是可能会有一位的进位影响，所以爆破一下就可以得到正确的ab。

得到ab后就可以得到a^2+b^2，就可以解出a和b了，然后就有p1_xor_q1_low的值。

之后就是一个剪枝+copper，由于给出了低402位所以完全没卡界，因此怎么快怎么来而不需要调epsilon。很快就能找到p1、q1然后计算flag。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
from Crypto.Util.number import *
from gmpy2 import *

e = 65537
delta = 61
n1 = 150838784531830142890659431841610000561921043629625618437510373123377520444955469509903631548754842609295975005302780725591929018884805452687677684641162979092069629817740554095750189248769936750051172301891394503776919559958638203717583333429953061416588208428893436430392654983424277005324307321992921302331
n2 = 102603788692700558034198259394482879736866145355211103067657972779629890324418113112441175321034955422723378003769267804892308121194871227786783930178021669484220789624643889449429959522560822967157677629720685465873700893389751397027159036419
c = 100199300622156732994823007073822662584719346985430234367094043002848132740563819931486477742264272832060136969084318984512567787814048659200236334994498141562184235841854521058494238451300610422156322926341430748222140189349893444976932184031798101999886029853099171189139509539715437105818418407563733036131

#part1 get p2
carrylist = [""] + [str(i) for i in range(10)]
for i in carrylist:
    try:
        ab = int(str(n2//10^(122+61)) + i + str(n2%10^61))
        a2_b2 = (n2 - ab*(10^122+1))//10^61
        temp = iroot((a2_b2 + 2*ab),2)[1]
        if(temp == True):
            aplusb = iroot(a2_b2 + 2*ab,2)[0]
            aminusb = iroot(a2_b2 - 2*ab,2)[0]
            a = (aplusb + aminusb) // 2
            b = aplusb - a
            p2 = a*10^61+b
            q2 = n2 // p2
            print(p2-delta)
            print(q2-delta)
    except:
        pass

leak = 10046182803426524264884288617724249912105444610090073402734131021321139584526984358095762482718044064584704548733703637802
#leak = 10213211395845269843580957624827180440645847045487337036378631004618280342652426488428861772424991210544461009007340273352


#part2 dfs and copper
leakbits = 402
a1 = bin(leak)[2:].zfill(leakbits)[::-1]
def find(p,q):
    l = len(p)
    mask = 2^l
    if(int(p,2)*int(q,2) % mask != n1 % mask):
        return

    if(l == leakbits):
        pp = int(p,2)
        PR.<x> = PolynomialRing(Zmod(n1))
        f = (2^leakbits)*x + pp
        f = f.monic()
        res = f.small_roots(X=2^(512-leakbits), beta=0.5)
        if(res):
            try:
                ph = int(res[0])
                p = (2^leakbits)*ph + pp
                q = n1 // p
                d = inverse(e,(p-1)*(q-1))
                print(long_to_bytes(int(pow(c,d,n1))))
            except:
                pass
                    
    else:
        if(a1[l] == "1"):
            find("1"+p,"0"+q)
            find("0"+p,"1"+q)
        else:
            find("0"+p,"0"+q)
            find("1"+p,"1"+q)

tempp = "1"
tempq = "1"
find(tempp,tempq)

#begin{just_the_beginning_of_the_RSA}



*ezcry

题目描述：

1
many ways to attack（flag格式为flag{}）

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# sage
from random import randint
inti_Con = [0x39a3f978106bac2d,0x2940e055f4a33725,0xfda9a7a293fb5bc9]
Con = [
    [0x9c52c2de7a9373c4,0xf2135cb886d0fa21,0x957df7f3cd4879e9],
    [0xd54f837d2738d717,0x400ddf1ffaae436d,0xc2abb601d9a26b07],
    [0x1904359f1deb3495,0xc21aa09ba52b157b,0x3d45525db1b19a0c],
    [0xed66cf26a65afc73,0x1cee569b29ffa476,0x3da45abf4304849 ]
]    

C = [
    [8  , -14, 7  ],
    [56 , -90, 35 ],
    [280, -434, 155]
]

p = 18446744073709551557
n = 12297829382473034371

def f(P:list, p:int, R:int, state = 0):
    X = [0 for i in range(3)]
    Y = [0 for i in range(3)]
    # 第一轮前加常数
    for i in range(3):
        X[i] = (P[i] + inti_Con[i]) % p
    # R轮轮常数迭代
    for r in range(1,R+1):
        for k in range(3):
            Y[k] = (C[k][0] * pow(X[0], 3, p) + C[k][1] * pow(X[1], n, p) + C[k][2] * pow(X[2], 3, p) + Con[(2*r-2) % 10][k]) % p
        for k in range(3):
            X[k] = (C[k][0] * pow(Y[0], n, p) + C[k][1] * pow(Y[1], 3, p) + C[k][2] * pow(Y[2], n, p) + Con[(2*r-1) % 10][k]) % p
    if state :
        return Y        
    else:
        return X

P = [randint(1,p), randint(1,p), 0] 
assert f(P, p, 2)[2] == 0
assert f(P, p, 1, 1)[1] == 1 
flag = 'flag{' + str(P[0]) + str(P[1]) + '}'
print()

题目是一个rescue prime的CICO(Constrained-input/constrained-output)问题。这里先放几个链接：

1143.pdf (iacr.org)

View of Algebraic Attacks against Some Arithmetization-Oriented Primitives (iacr.org)

slides.pdf (iacr.org)

其中，第一个是rescue prime的实现论文，第二个是关于一些CICO问题的攻击论文，第三个是第二篇论文的ppt展示形式。

而这个问题之前在香山杯见过，不过当时看到的所有wp都是非预期解的，所以没有想着去学习一下预期思路，就带帐了。没有想到还能遇见。

那这次就好好学习一下吧，我们先从标准形式的rescue prime的实现过程以及攻击方式来讲。这里我会尽量用最简洁易懂的语言来说明，具体的详细参考可以看论文。理解的很粗浅，有错误欢迎各位师傅指出。

rescue prime

rescue prime的实现过程大致如下，这里我们选取输入是三元组、轮次为R轮的形式来说明。首先要定义一些常量：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
inti_Con = [0x39a3f978106bac2d,0x2940e055f4a33725,0xfda9a7a293fb5bc9]
Con = [
    [0x9c52c2de7a9373c4,0xf2135cb886d0fa21,0x957df7f3cd4879e9],
    [0xd54f837d2738d717,0x400ddf1ffaae436d,0xc2abb601d9a26b07],
    [0x1904359f1deb3495,0xc21aa09ba52b157b,0x3d45525db1b19a0c],
    [0xed66cf26a65afc73,0x1cee569b29ffa476,0x3da45abf4304849 ]
]    

C = [
    [8  , -14, 7  ],
    [56 , -90, 35 ],
    [280, -434, 155]
]

p = 18446744073709551557
n = 12297829382473034371

这些常数的作用是什么之后都会讲到，而首先需要知道p的作用。p是64bit能表示的最大素数，也就作为整个实现过程的有限域，也就是说所有运算都在模p下进行。

那么对于输入的三元组 (m1,m2,m3)来说，他首先需要加上初始常数inti_Con，得到第一轮前的输入状态，我们记为 (X01,X02,X03) 。为了之后的流程看上去更直观，在之后的每个三元组状态都会用列向量的形式来表示，也就是：

然后就进入到R轮的操作中。对于每一轮来说其实都可以看作是一个状态到另一个状态的转变，因此我们对于第i轮，可以将第i轮的输入输出分别记作：

而每一轮内部其实也涉及到一个中间状态，记为：

那么就先分开看这两部分的变换。首先，对于输入到中间状态，其变换是：

其中，C和Con就是上面给出的常数的对应部分，C对应的矩阵乘法也就是论文里的MDS变换，而Con对应论文里的AddC变换。而S也是一个变换，他表示的含义是将三元组中的每个元素都取三次方。

而中间状态到输出状态的变换是：

最大的变化是S变成了invS，而invS的含义是将三元组中的每个元素都取1/3次方。而在模p下的乘1/3次方的操作其实也就对应了乘n次方，n也就是上面给出的那个常数。除此之外Con的具体取值也发生了变化。

然后就是进行R轮这样的操作，就得到最终输出。到这里，rescue prime的完整实现和上面所有常数的作用就都说完了。

接下来就是rescue prime的CICO问题是什么，以及该怎么进行寻找。

CICO

对于三元组形式的rescue prime，其问题可以描述为找到符合下面形式的输入输出对：

先不管这个题目，我们这里考虑最简单的标准rescue prime的两轮情形。对于第一轮前，可以写作是：

由于P到X0的变换仅仅是加了常数，所以不需要管他，我们就关注如下过程：

此时我们就需要把整个变换过程展开一下，对于前半截是：

对于后半截：

我们把S盒展开，直接写成里面的元素乘方的形式：

相应的逆S盒就有：

而我们的核心思想是造多项式，然后groebner求这些多元方程组的解。我们将每个状态向量都视为由三个变量组成，那么比如对于第一个过程，他就可以写作三个如下形式的度为3的多项式：

很顺利地就列出了三个度为3的多项式。那么第二步呢？因为第二步涉及到1/3次方，实际上也就是n次方，而高次项出现在groebner里是很灾难的 。所以要想办法转化一下，转化的思路就是把过程逆着写一遍：

这样一来就可以把左边的逆S盒操作变成右边的S盒操作了，也就是：

这样就又能写出度为3的多项式。

而由上面的过程可以观察到，对于每两个状态之间，我们都可以写出三个度为3的多项式，所以将全部状态都看作三个变量组成的话，我们可以列出15个变量构成的12个多项式。而对于CICO问题来说，我们相当于知道其中两个变量的值，因此最终得到的是13个变量构成的12个多项式，因此一定有多解。

实际上，我们还可以观察到所有的Y其实也都只是中间量，我们的多项式中完全可以不用这些变量来造多项式。而消去这些变量的方式也很容易，我们只需要把由每个Y联系起来的两个式子简单作个差就行了。

但是这样仍是变量多于方程数，而我们知道我们其实只需要找到一组解就可以。为此论文里提出了一种可以bypass第一轮的办法，采取的手段是固定一个状态的值使得方程恒有解，这样找到一组解之后还可以迭代找到其他解。而这就不是这篇文章里要讨论的重点了，有兴趣的师傅可以参考论文。

那么大致理解寻找的思路过后，我们终于回头来看看这个题目本身。

题目

题目相比于标准的rescue prime来说，作了如下两点改动：

  • S盒和逆S盒不再是(3,3,3)和(1/3,1/3,1/3)，而是变成(3,1/3,3)和(1/3,3,1/3)

  • 多给出了一个变量值，也就是Y12=1

既然多给了一个值，那么用刚才的想法去想，应该能造出十二个变量十二个多项式，因此解应该是唯一的。现在的问题就是在变换了S盒和逆S盒后，怎么构造出这些多项式。

最直接的想法依然是把所有状态视作三个变量组成，而对于S盒来说，他的改变其实区别并不大，这是因为我们只需要把3次的项正着思考，1/3的项倒着思考成后面多项式的三次方就行了。不妨拿第一轮的前半截变换举个简单的例子：

把除去S盒，剩余的所有变换写到右侧去：

那么我们就可以列出如下三个多项式：

其余的也就同理了。这样就能造出15个变量构成的12个多项式。并且由于三个值已知，实际上也就是12个变量构成的12个多项式。这一部分的实现脚本如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
from Crypto.Util.number import *
from tqdm import *
from random import *

inti_Con = [0x39a3f978106bac2d,0x2940e055f4a33725,0xfda9a7a293fb5bc9]
Con = [
    [0x9c52c2de7a9373c4,0xf2135cb886d0fa21,0x957df7f3cd4879e9],
    [0xd54f837d2738d717,0x400ddf1ffaae436d,0xc2abb601d9a26b07],
    [0x1904359f1deb3495,0xc21aa09ba52b157b,0x3d45525db1b19a0c],
    [0xed66cf26a65afc73,0x1cee569b29ffa476,0x3da45abf4304849 ]
]    

C = [
    [8  , -14, 7  ],
    [56 , -90, 35 ],
    [280, -434, 155]
]

p = 18446744073709551557
n = 12297829382473034371

C = Matrix(Zmod(p),C)
inv_C = Matrix(Zmod(p),C)^(-1)

if(1):
    PR.<X01,X02,X03,Y11,Y12,Y13,X11,X12,X13,Y21,Y22,Y23,X21,X22,X23> = PolynomialRing(Zmod(p))

    #init
    f0 = X03 - 0

    #Round 1
    r = 1

    C20 = inv_C[2,0]*Con[(2*1-2) % 10][0] + inv_C[2,1]*Con[(2*1-2) % 10][1] + inv_C[2,2]*Con[(2*1-2) % 10][2]
    t = C20 + inti_Con[2]^3

    f1 = Y12 - 1
    k = 0
    f2 = inv_C[k,0]*(Y11-Con[(2*r-2) % 10][0])+inv_C[k,1]*(Y12-Con[(2*r-2) % 10][1])+inv_C[k,2]*(Y13-Con[(2*r-2) % 10][2]) - (X01+inti_Con[0])^3
    k = 1
    f3 = (inv_C[k,0]*(Y11-Con[(2*r-2) % 10][0])+inv_C[k,1]*(Y12-Con[(2*r-2) % 10][1])+inv_C[k,2]*(Y13-Con[(2*r-2) % 10][2]))^3 - (X02+inti_Con[1])
    k = 2
    f4 = inv_C[k,0]*(Y11-Con[(2*r-2) % 10][0])+inv_C[k,1]*(Y12-Con[(2*r-2) % 10][1])+inv_C[k,2]*(Y13-Con[(2*r-2) % 10][2]) - (X03+inti_Con[2])^3

    k = 0
    f5 = (inv_C[k,0]*(X11-Con[(2*r-1) % 10][0])+inv_C[k,1]*(X12-Con[(2*r-1) % 10][1])+inv_C[k,2]*(X13-Con[(2*r-1) % 10][2]))^3 - Y11
    k = 1
    f6 = inv_C[k,0]*(X11-Con[(2*r-1) % 10][0])+inv_C[k,1]*(X12-Con[(2*r-1) % 10][1])+inv_C[k,2]*(X13-Con[(2*r-1) % 10][2]) - Y12^3
    k = 2
    f7 = (inv_C[k,0]*(X11-Con[(2*r-1) % 10][0])+inv_C[k,1]*(X12-Con[(2*r-1) % 10][1])+inv_C[k,2]*(X13-Con[(2*r-1) % 10][2]))^3 - Y13


    #Round 2
    r = 2

    k = 0
    f8 = inv_C[k,0]*(Y21-Con[(2*r-2) % 10][0])+inv_C[k,1]*(Y22-Con[(2*r-2) % 10][1])+inv_C[k,2]*(Y23-Con[(2*r-2) % 10][2]) - X11^3
    k = 1
    f9 = (inv_C[k,0]*(Y21-Con[(2*r-2) % 10][0])+inv_C[k,1]*(Y22-Con[(2*r-2) % 10][1])+inv_C[k,2]*(Y23-Con[(2*r-2) % 10][2]))^3 - X12
    k = 2
    f10 = inv_C[k,0]*(Y21-Con[(2*r-2) % 10][0])+inv_C[k,1]*(Y22-Con[(2*r-2) % 10][1])+inv_C[k,2]*(Y23-Con[(2*r-2) % 10][2]) - X13^3

    f11 = X23 - 0
    k = 0
    f12 = (inv_C[k,0]*(X21-Con[(2*r-1) % 10][0])+inv_C[k,1]*(X22-Con[(2*r-1) % 10][1])+inv_C[k,2]*(X23-Con[(2*r-1) % 10][2]))^3 - Y21
    k = 1
    f13 = inv_C[k,0]*(X21-Con[(2*r-1) % 10][0])+inv_C[k,1]*(X22-Con[(2*r-1) % 10][1])+inv_C[k,2]*(X23-Con[(2*r-1) % 10][2]) - Y22^3
    k = 2
    f14 = (inv_C[k,0]*(X21-Con[(2*r-1) % 10][0])+inv_C[k,1]*(X22-Con[(2*r-1) % 10][1])+inv_C[k,2]*(X23-Con[(2*r-1) % 10][2]))^3 - Y23


    #groebner
    #f15 = X13 - 0
    F = [f0,f1,f2,f3,f4,f5,f6,f7,f8,f9,f10,f11,f12,f13,f14]
    res = Ideal(F).groebner_basis()
    if(res != [1]):
        for i in res:
            if(len(list(i)) < 15):
                print(i)

然而这样sage虽然很快就能算出来(1min左右)，但他算出的结果并不含单变量的同余方程，没有办法解出结果来，想了很久也没想出好办法，也没想通是为什么，就去问了出题人cot287师傅，然后又得到了新的思路。其实这里面的很多变量都是不需要的。具体来说，我们首先就可以去除掉X01和X02，以及X21和X22，也就是只用如下过程来构造多项式：

然后还有一点是，我们把Y对应的状态看作是如下向量：

这是为了便于后续的乘三次方和开三次方的操作，如此替换为三个变量m、n、o就可以有效避开1/3带来的困扰。而我们最终就可以列出仅由m1、o1、m2、n2、o2构成的五个多项式，构造思路和前面区别不大，只是把中间的X11、X12、X13状态给消去。

反正一共就五个方程，干脆把列的过程全部写出来好了。我们设五个变量m1、o1、m2、n2、o2，他们分别满足：

然后第一个多项式是由这个变换列出：

由于我们只想列出关于已知的X03的多项式，所以变换需要倒过来看，也就是：

然后就使用最后一行构成的等式就可以造出第一个多项式：

1
2
3
n1 = 1
X03 = 0
f1 = inv_C[2,0]*(m1^3-Con[0][0])+inv_C[2,1]*(n1-Con[0][1])+inv_C[2,2]*(o1^3-Con[0][2]) - (X03+inti_Con[2])^3

第二个多项式用最后的变换造：

变换可以看作：

仍然是只用X23构成的那一个多项式即可(因为已知他是0)，这就造出了第二个方程：

1
f2 = C[2,0]*m2+C[2,1]*n2^3+C[2,2]*o2+Con[3][2]

剩下三个方程就是由中间的变换来造的：

中间的X11、X12、X13是我们不需要的，他只用来把两边的Y对应状态联系起来而已，所以要想办法消去。消去方式就是，一个看作正向，一个看作反向，视作如下变换：

这样就可以造出三个多项式如下：

1
2
3
f3 = (C[0,0]*m1+C[0,1]*n1^3+C[0,2]*o1+Con[1][0])^3 - (inv_C[0,0]*(m2^3-Con[2][0])+inv_C[0,1]*(n2-Con[2][1])+inv_C[0,2]*(o2^3-Con[2][2]))
f4 = (C[1,0]*m1+C[1,1]*n1^3+C[1,2]*o1+Con[1][1])   - (inv_C[1,0]*(m2^3-Con[2][0])+inv_C[1,1]*(n2-Con[2][1])+inv_C[1,2]*(o2^3-Con[2][2]))^3
f5 = (C[2,0]*m1+C[2,1]*n1^3+C[2,2]*o1+Con[1][2])^3 - (inv_C[2,0]*(m2^3-Con[2][0])+inv_C[2,1]*(n2-Con[2][1])+inv_C[2,2]*(o2^3-Con[2][2]))

这里就可能会存在一点问题了，因为出现了度为9的多项式，可能会显著提高groebner的复杂度。同时会出现形如xyz这样多个变量相乘的形式，正则度可能不太高(cot师傅说正则度也会影响groebner基的求解)。不过的确还没想到什么优化，先继续往下吧。

这一部分具体实现可以参考下面：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from Crypto.Util.number import *
from tqdm import *
from random import *

inti_Con = [0x39a3f978106bac2d,0x2940e055f4a33725,0xfda9a7a293fb5bc9]
Con = [
    [0x9c52c2de7a9373c4,0xf2135cb886d0fa21,0x957df7f3cd4879e9],
    [0xd54f837d2738d717,0x400ddf1ffaae436d,0xc2abb601d9a26b07],
    [0x1904359f1deb3495,0xc21aa09ba52b157b,0x3d45525db1b19a0c],
    [0xed66cf26a65afc73,0x1cee569b29ffa476,0x3da45abf4304849 ]
]    

C = [
    [8  , -14, 7  ],
    [56 , -90, 35 ],
    [280, -434, 155]
]

p = 18446744073709551557
n = 12297829382473034371

C = Matrix(Zmod(p),C)
inv_C = Matrix(Zmod(p),C)^(-1)

PR.<m1,o1,m2,n2,o2> = PolynomialRing(Zmod(p))

n1 = 1
X03 = 0

#init
f1 = inv_C[2,0]*(m1^3-Con[0][0])+inv_C[2,1]*(n1-Con[0][1])+inv_C[2,2]*(o1^3-Con[0][2]) - (X03+inti_Con[2])^3

#final
f2 = C[2,0]*m2+C[2,1]*n2^3+C[2,2]*o2+Con[3][2]

#middle
f3 = (C[0,0]*m1+C[0,1]*n1^3+C[0,2]*o1+Con[1][0])^3 - (inv_C[0,0]*(m2^3-Con[2][0])+inv_C[0,1]*(n2-Con[2][1])+inv_C[0,2]*(o2^3-Con[2][2]))
f4 = (C[1,0]*m1+C[1,1]*n1^3+C[1,2]*o1+Con[1][1])   - (inv_C[1,0]*(m2^3-Con[2][0])+inv_C[1,1]*(n2-Con[2][1])+inv_C[1,2]*(o2^3-Con[2][2]))^3
f5 = (C[2,0]*m1+C[2,1]*n1^3+C[2,2]*o1+Con[1][2])^3 - (inv_C[2,0]*(m2^3-Con[2][0])+inv_C[2,1]*(n2-Con[2][1])+inv_C[2,2]*(o2^3-Con[2][2]))

print(f1)
print(f2)
print(f3)
print(f4)
print(f5)

但这样造出五个多项式后，给sage跑groebner，还是不行。然后就又去问cot师傅，了解到他是用maple跑的，因为maple的groebner写的更好一些。同时maple的groebner是可以设序的(后面了解到sage也可以，就在定义多项式变量的时候设置序就行)，并且可以做一些对方程结构和序做一些优化，让groebner跑得更快。不过cot师傅的做法是用结式，因为结式在他当时密码挑战赛时表现优于groebner。

又学到好东西了，折腾一下，下一个15天的maple试用版试了试，发现确实是对groebner理解太浅显了，除了知道它可以用于消元外基本上一无所知，所以也找不到好方法优化多项式组，也不知道什么才是合适的序，所以怎么折腾都跑不出想要的结果。然后也试了试用resultant去两两消元，最后也没试明白。

主要问题就在于：完全不了解多项式的序对groebner的影响，所以不知道怎么构造合适的序，怎么根据序去调整方程结构；并且多项式本身可能还可以做一些诸如降低他的度、或是提升他的正则度的优化，但是我没想到。

所以还是要多学啊。之后如果跑出结果来的话会回来更新。

(2.7更新)

官方wp出了，拿出题人的exp上maple跑了一遍，发现不到3min就可以跑出结果：

image-20240207000201080

然后发现一件事情，求出来的groebner基并不是想象中的几个单元单次多项式，而是几个单元高次(729次)多项式：

image-20240207000303392

这说明还要对groebner基中的每个多项式求根才能得到变量值。所以昨晚上不一定是没求出groebner基，而是基太长了，打印不出来，只能说对groebner、多项式以及maple软件的了解都太欠缺了。

然后观察出题人造的方程形式，确实是与上面的五个变量五个多项式是一模一样的，只是他设置的项序是(n2, o1, m1, o2, m2)。而因为我并不熟悉maple的其他命令，所以我选择先让sage造出这五个多项式，并且打印出来：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from Crypto.Util.number import *
from tqdm import *
from random import *

inti_Con = [0x39a3f978106bac2d,0x2940e055f4a33725,0xfda9a7a293fb5bc9]
Con = [
    [0x9c52c2de7a9373c4,0xf2135cb886d0fa21,0x957df7f3cd4879e9],
    [0xd54f837d2738d717,0x400ddf1ffaae436d,0xc2abb601d9a26b07],
    [0x1904359f1deb3495,0xc21aa09ba52b157b,0x3d45525db1b19a0c],
    [0xed66cf26a65afc73,0x1cee569b29ffa476,0x3da45abf4304849 ]
]    

C = [
    [8  , -14, 7  ],
    [56 , -90, 35 ],
    [280, -434, 155]
]

p = 18446744073709551557
n = 12297829382473034371

C = Matrix(Zmod(p),C)
inv_C = Matrix(Zmod(p),C)^(-1)

PR.<m2,o2,m1,o1,n2> = PolynomialRing(Zmod(p))

n1 = 1
X03 = 0

#init
f1 = inv_C[2,0]*(m1^3-Con[0][0])+inv_C[2,1]*(n1-Con[0][1])+inv_C[2,2]*(o1^3-Con[0][2]) - (X03+inti_Con[2])^3

#final
f5 = C[2,0]*m2+C[2,1]*n2^3+C[2,2]*o2+Con[3][2]

#middle
f2 = (C[0,0]*m1+C[0,1]*n1^3+C[0,2]*o1+Con[1][0])^3 - (inv_C[0,0]*(m2^3-Con[2][0])+inv_C[0,1]*(n2-Con[2][1])+inv_C[0,2]*(o2^3-Con[2][2]))
f3 = (C[1,0]*m1+C[1,1]*n1^3+C[1,2]*o1+Con[1][1])   - (inv_C[1,0]*(m2^3-Con[2][0])+inv_C[1,1]*(n2-Con[2][1])+inv_C[1,2]*(o2^3-Con[2][2]))^3
f4 = (C[2,0]*m1+C[2,1]*n1^3+C[2,2]*o1+Con[1][2])^3 - (inv_C[2,0]*(m2^3-Con[2][0])+inv_C[2,1]*(n2-Con[2][1])+inv_C[2,2]*(o2^3-Con[2][2]))

print(f1)
print(f2)
print(f3)
print(f4)
print(f5)

然后粘贴到maple里去求groebner基：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
>with(LinearAlgebra);
with(Groebner);

>f1 := 4611686018427387891*m1^3 + 6917529027641081834*o1^3 + 8993434471925015234;
f2 := 512*m1^3 + 1344*m1^2*o1 + 1176*m1*o1^2 + 8935141660703064033*m2^3 + 343*o1^3 + 10232178353385766879*o2^3 + 18132228624049335141*m1^2 + 17896342036804172829*m1*o1 + 8982571145708672585*o1^2 + 13489782848274234489*m1 + 17726168133330272201*n2 + 4886030964598873344*o1 + 8558003665055786614;
f3 := 16424627841020198849*m2^9 + 3082713944935104499*m2^6*o2^3 + 5842294616606375917*m2^3*o2^6 + 11877681067236261850*o2^9 + 14440792205163495398*m2^6*n2 + 6577507255774609391*m2^3*n2*o2^3 + 16008607825441849293*n2*o2^6 + 2315200782863393558*m2^6 + 4152388971314589023*m2^3*o2^3 + 1129956652251207029*o2^6 + 1257630195943210991*m2^3*n2^2 + 13038483871191007189*n2^2*o2^3 + 15470057352885188411*m2^3*n2 + 14459726586885204931*n2*o2^3 + 13362083559747081110*m2^3 + 3683381545235644407*n2^3 + 1336208355974708111*o2^3 + 7544915043732670853*n2^2 + 56*m1 + 9856833213872142272*n2 + 35*o1 + 8675376255439944131;
f4 := 21952000*m1^3 + 36456000*m1^2*o1 + 20181000*m1*o1^2 + 13835058055282163666*m2^3 + 3723875*o1^3 + 11529215046068469723*o2^3 + 13795409458218062279*m1^2 + 11979427601293291888*m1*o1 + 3315734425357964719*o1^2 + 15953492053777220513*m1 + 11529215046068469724*n2 + 10478428107779314173*o1 + 6698939315313186010;
f5 := 18446744073709551123*n2^3 + 280*m2 + 155*o2 + 277610931875235913;

>p := 18446744073709551557;
gb := Basis({f1, f2, f3, f4, f5}, plex(n2, o1, m1, o2, m2), characteristic = p);
solution := msolve({gb[1], gb[2], gb[3], gb[4], gb[5]}, p);
print(solution);
m2 := subs(solution, m2);

求出几个变量的解：

image-20240207000800150

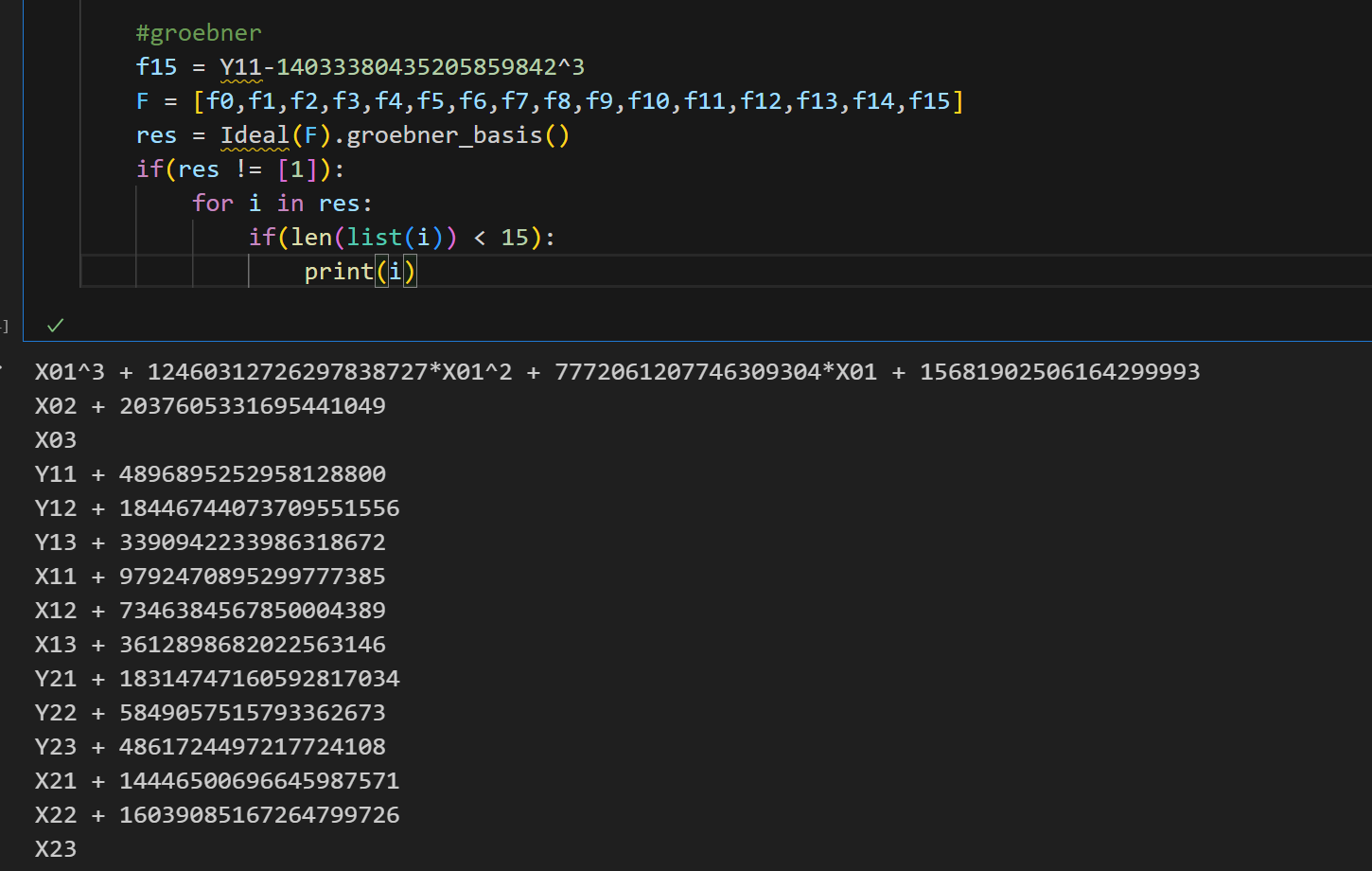
然后随便粘一个值，粘回上面写的那个sage的12变量12多项式的脚本，再求groebner就能求出所有状态，也就有初始状态了：

image-20240207001143036

得到初始状态是：

1
2
X01 = 5828164276169944109
X02 = 16409138742014110508

代进加密脚本check一下的确能通过。所以flag就是：

1
flag{582816427616994410916409138742014110508}

真的是一道非常有意思，但是对我来说很艰难的一道题目。了解到很多新鲜的东西，收获很多，也知道了自己很多不足。