夺冠!
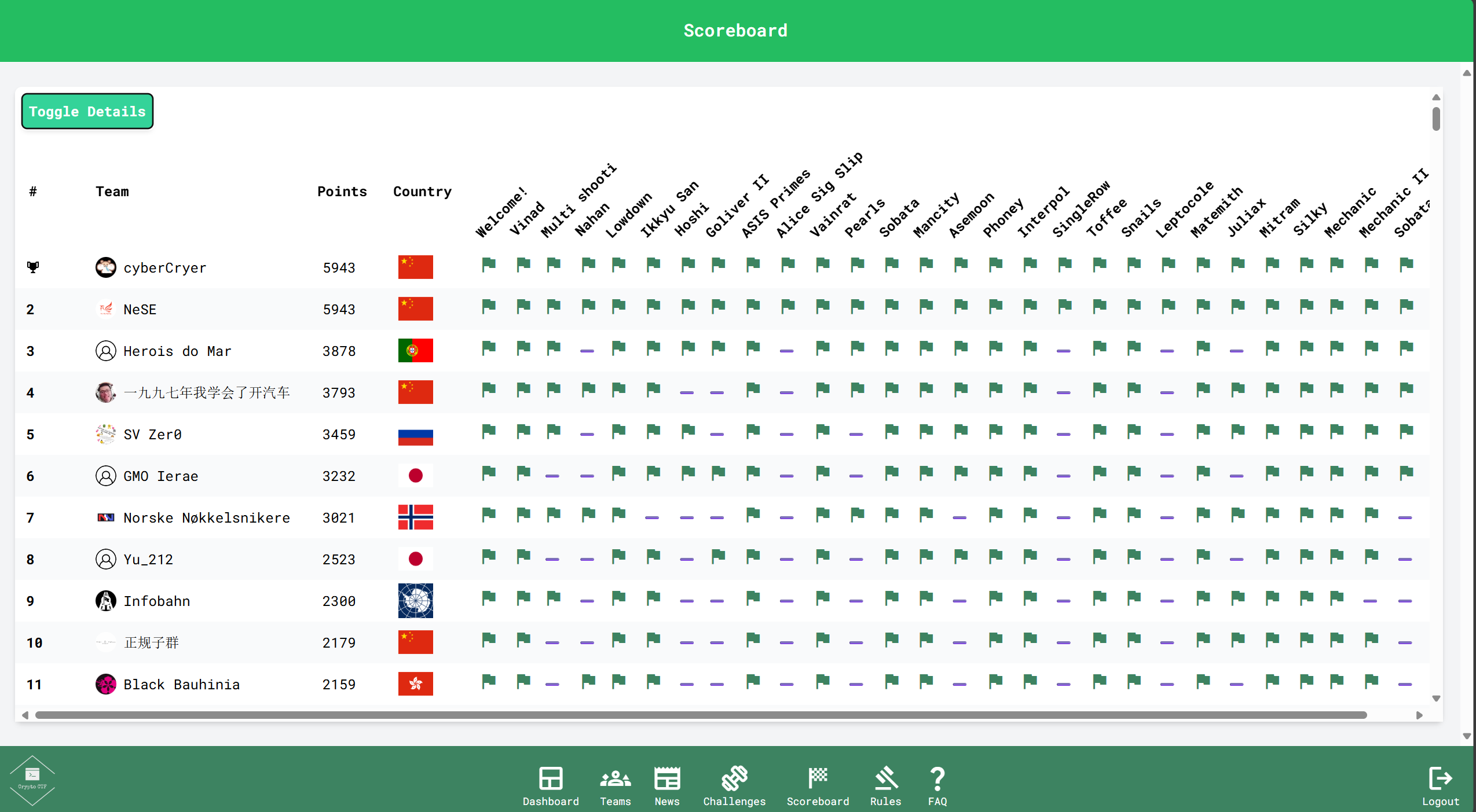
@Aqua Cat和@Q7实在太猛,赛中好多题都没来得及看就被秒了,所以不少题复现的时候都要从零开始看,流程比较长,所以这篇wp自然就有点拖。
不过也确实很摸 (=´ω`=)
输出文件就都不放了,需要的师傅应该还可以在CRYPTO CTF下载到,或者直接找我拿也行。
Warm-up
Welcome! 👋(361 solves , 27 pts)
题目
题目描述:
1 | Welcome! |
思路
后半段base64解掉:
1 | flag{w3lc0m3_T0_7h3_m4dh0u5e_h4v3_4_S4n17y_5Andw1ch!} |
Easy-Peasy
Vinad(211 solves , 34 pts)
题目
题目描述:
1 | Vinad's ‘random’ keys are as unpredictable as a cat. Poke its weak spots, steal the flag—chaos included! |
题目:
1 | #!/usr/bin/env python3 |
题目流程如下:
- 生成一个长度为512,其中每个数字均为512bit随机数的列表
R以及一个512bit的随机数r - 计算
p = vinad(r, R)以及e = vinad(r + 0x10001, R) - 给出
R及公钥n,要求分解n,解RSA得到flag
思路
对于vinad函数,其输出的每一比特其实可以看作是x与对应位置的ri在$GF(2)$下向量相加,得到的向量再与全1向量在$GF(2)$下相乘的结果。照这个思路可以把该函数写成一个$GF(2)$下的矩阵方程如下:
把这个矩阵方程拆开就知道最后输出的结果只会与输入x的1的数量有关系,所以对于确定的R来说,其vinad的输出只会有两种可能,因此e和p均在这两种可能中,就可以很轻松的解掉RSA。
exp
1 | from Crypto.Util.number import * |
Interpol(129 solves , 45 pts)
题目
题目描述:
1 | Only brute force won't crack Interpol! Its massive polynomial guards the flag fiercely. |
题目:
1 | #!/usr/bin/env sage |
题目用很奇怪的randpos函数生成了若干个$Q[x]$上的点对,这些点对中部分点的纵坐标和flag字符相关,最后将这些点对插值成一个$Q[x]$上的多项式$f(x)$,要求还原flag。
思路
看上去randpos略有点复杂, 但实际上,其中有用的仅有randint(0,1)=1的那个分支的点对,而这些点的坐标总是绝对值不超过flag长度的负数,因此爆破flag长度,并在$f(x)$上逐个代入这些横坐标,得到的纵坐标是ASCII码值时就可以得到n以及对应的flag字符和索引。
exp
1 | from Crypto.Util.number import * |
Mechanic(109 solves , 50 pts)
题目
题目描述:
1 | Mechanic’s ‘post-quantum’ lock is so easy, even Schrödinger’s cat could crack it, alive and dead. |
题目:
1 | #!/usr/bin/env python3 |
题目基于MLKEM_1024,随机生成了一个二进制长度为40的比特串,并根据每一比特具体是0还是1进行如下操作:
- 当前bit为1,生成MLKEM_1024的一对公私钥
pkey和skey,将当前明文文件进行加密,并将密文文件作为新的明文文件用于下一次加密 - 当前bit为0,生成和合法公私钥相同长度的随机串
pkey和skey
并且每一次都将skey写入到output.raw里,要求还原最初的明文文件flag.png。
思路
要想每一轮都能正常解密,主要就是要区分bit为0生成的随机的skey和真正合法的skey的区别,问一下Gemini会知道skey中会有pkey和h(pkey)的部分,因此可以对每个skey做这样的检验就知道是不是合法skey了。
exp
1 | from quantcrypt.kem import MLKEM_1024 |
Getting There
Mancity(98 solves , 54 pts)
题目
题目描述:
1 | Decipher Mancity by exploiting RSA modulus secrets, bit by bit, relation by relation. |
题目:
1 | #!/usr/bin/env python3 |
题目要分解RSA的公钥n,而组成n的两个素数生成方式满足:
- 先生成256bit的随机素数$p$
- 将$p$的每一bit扩展成两位组成$r$,扩展方式为每一bit后面加一个1
- 将$p$后面加上256个1,得到$q$
- $n = qr$
思路
很显然是一个剪枝问题,由于低位有$q$的256个1干扰,所以从高位搜索$p$的比特位即可。
exp
1 | from Crypto.Util.number import * |
Vainrat(67 solves , 72 pts)
题目
题目描述:
1 | Precision is key, Vainrat escapes sluggish calculators effortlessly. |
题目:
1 | #!/usr/bin/env sage |
记flag长度为$t$,其对应大整数值为$m$,题目主要流程如下:
生成精度为440的实数域$R$
$x_0 = 10^{-t}m$,$y_0$为$R$上的随机元素取绝对值,给出$y_0$
可无限次进行如下迭代:
当迭代次数超过12次时,就有机会获得当前的$y_i$,当超过19次时则一定能获得当前$y_i$,要求还原flag。
思路
由于当超过19次后,我们一定能连续获得每一轮的$y_i$,而关于$x_i$则没有什么信息,因此要考虑的是消去$x_i$,从而把$y_i$关联起来向前回推。
不妨拿$y_1,y_2,y_3$做例子,可以做如下推导:
所以也就有$y_1 = \frac{y_2^3}{2y_3^2 - y_2^2}$成立,因此可以从得到的连续的$y$开始,反复迭代回去,直到求出所有的$y_i$来。
求完所有$y_i$后自然有$y_1$,结合本身就有的$y_0$,可以利用$y_1 = (\frac{x_{0}+y_{0}}{2}y_{0})^{\frac{1}{2}}$求出$x_0$,也就得到了flag。需要注意的是这里m的长度是flag转为大整数后再转为字符串的长度,所以爆破范围需要大一些。
exp
1 | from Crypto.Util.number import * |
Matemith(59 solves , 80 pts)
题目
题目描述:
1 | Solving Matemith’s polynomial equations is easier than pronouncing ‘Matemith’, but that’s not saying much! |
题目:
1 | #!/usr/bin/env sage |
题目定义了六个变量$u,v,w,x,y,z$以及六个关于变量的方程$f,g,h,i,j,k$,将flag分为六个14字节的部分并代入六个变量中,得到$GF(p)$下$f,g,h,i,j,k$对应的六个等式,要求解出六个变量值从而还原完整flag。
思路
六个变量六个方程,但是方程不是线性的,所以第一思路就是用groebner试一试:
1 | R.<u, v, w, x, y, z> = PolynomialRing(GF(p)) |
可以发现并不能直接得到解,但可以得到下面几个单项构成的新等式:
1 | [y*z^2, y*z, z^2, x, y, z, 1] |
而最后三个等式是线性的,而由于flag的每个部分只有14x8=112bit,在$GF(p)$下是小量,所以可以造格求解一波。
格出来的东西和目标向量$(x,y,z,1,u,v,w)$有一定区别,前三个值做过约简,但可以有$u,v,w$的准确值。
有了这个准确值后,理想中再代回去求一次groebner就行,或者也可以直接解线性方程。但试了一下代回去groebner发现虽然解不出来,但是简化后的多项式的单项变成了:
1 | [y^2, y, z, 1] |
由于模数$p$是素数,所以稍微手动一下resultant求根就可以求出$x,y,z$。
exp
1 | R.<u, v, w, x, y, z> = PolynomialRing(GF(p)) |
1 | v1 = [1, 9278059260927794625321822521445150709925989348199550227539018734257217333155253421906997535184, 8448761634028956410528911781238729498451220906568524310219824841324137446537586214296021618303, 8832923846876892468664467862366245924256914356941763689573886659181473460260016336177890742462, 6222026266229455098581548668905780547435323354175322166684186804438675930293185506378599302869] |
1 | res = Ideal([f, g, h, i, j, k, u-U, v-V, w-W]).groebner_basis() |
1 | ff1 = res[0] |
1 | res = Ideal([f, g, h, i, j, k, u-U, v-V, w-W, y-Y, z-Z]).groebner_basis() |
1 | X = p - 9892984422801315119260311427714389408772405421306235794826916608345176797419211841055778587142 |
其他
为什么直接groebner会出不来呢?后来想了一下原因,觉得和后面的Goliver_II这个题原因也许一样:这个形式的方程一定有多解——也就是resultant之后的那个高次多项式的另外的根,也都是这个多项式系统的解之一,所以是不可能groebner出一个一次多项式直接得到所有变量的值的。
然后就是flag说的CSIDH-HNP,才想起昨年帮@yolbby验题的时候看过的这篇,可能是因为这题模仿了这篇里构造的等式结构。
不过@yolbby昨年想出的CIHNP恰好在WMCTF赛前不久被idekCTF出掉了XD
Sobata(44 solves , 102 pts)
题目
题目描述:
1 | Master Sobata by dissecting ECC secrets, then tame its walk function’s hidden path. |
题目:
1 | #!/usr/bin/env sage |
题目基于ECC,其基本信息有:
- 生成参数$p,a,b,c,d$,其中$p$为512bit的素数,$a,b$分别为$Z_p^*$下的三阶和二阶元素,$c,d$均为$Z_p$下的随机值
- 生成曲线
E = EllipticCurve(GF(p), [0, d]) - 将flag的大整数值$m$做lift到曲线$E$上,记该点为$P$
- 定义一个
walk函数,其接受曲线$E$上的一点$(x,y)$作为输入,输出$c\cdot (ax,by)$ - 定义一个
jump函数,其接受曲线$E$上的一点$(x,y)$以及一个数字$n$作为输入,输出
在此基础上,我们有无限次的交互机会:
- 输入
e,可以获得walk(P)的值 - 输入
w,可以给定曲线$E$上的一点$Q$,靶机回复walk(Q)的值 - 输入
j,可以给定曲线$E$上的一点$Q$以及一个数字$n$,靶机回复jump(Q, n)的值
要求还原flag。
思路
由于题目在交互前啥都不给,所以要先求出曲线参数才行。最开始我们输入e能获得曲线$E$上的一点,对该点反复向后walk就可以获得曲线上的很多点,所以恢复参数不是问题。
而由于$a,b$阶都很小,所以基本可以算是知道,因此要从walk(P)获得flag的话,大概可以有两个出发点:
- 直接把$c$想办法求出来
- 想办法利用
walk或jump把$c$消掉
这里可以把walk看作是两个映射的复合:第一个映射是$\phi:(x,y)\rightarrow (ax,by)$,这是曲线$E$上的自同态;第二个映射则就是普通的$[c]$,只是$c$未知。由于$a,b$的阶分别为3,2,所以$\phi^6$是一个恒等变换,这两种映射是可交换的。
可以看出第二条路非常容易走通,我们只需要令$n$为-1,就可以直接jump回初始点,然后小爆一下$a,b$就可以得到其横坐标了。
exp
1 | from Crypto.Util.number import * |
ASIS Primes(40 solves , 110 pts)
题目
题目描述:
1 | ASIS Primes is a cryptography challenge requiring primes with printable, meaningful bytes; can you generate such primes effectively? |
题目:
1 | #!/usr/bin/env python3 |
题目大意可以理解为:
- 生成两组前缀
- 需要给出素数$p,q$,这两个素数转为字节串后需满足:
- 前缀分别为给定前缀
- 均以
}结尾 - 所有字符均需要在指定字符集
string.printable[:63] + '_{-}'中 - 比特长度要求
(9 * _p * _q).bit_length() == 2 * nbit
- 给出符合要求的$p,q$后,题目就会用65536当作加密指数,输入的$p,q$当作私钥对flag加密并给出密文。
思路
每失败提交一次,nbit就会对应增大1,所以可以先把nbit刷大一点。
之后似乎除了硬爆好像也没啥好办法TT,这个比特长度还有点小麻烦,所以偷懒直接贴@Q7当时比赛的数据好了。65536的指数用nth_root就行
exp
1 | from Crypto.Util.number import * |
Ikkyu San(31 solves , 134 pts)
题目
题目描述:
1 | Ikkyu San, a sage child, developed a unique crypto-system that helps young CTF players identify and choose talented individuals. |
题目:
1 | #!/usr/bin/env sage |
依然是ECC的题目,流程为:
生成256bit的素数$q$,以及$GF(p)$下的随机值$a,b$,并用$a,b$生成曲线$E$
生成曲线$E$上的两个随机点$G,H$
题目对$E$有些奇怪的要求:
- 横坐标1不能在曲线上
- $b-a-1$不能是二次剩余
但是我的做法似乎都没用到
此外还定义了一个
fongi函数,不妨记为$f$,对于作为输入的$E$上的点$P$,返回$f(P) = x_PG + y_PH + x_GP$
参数生成完后,我们有无限次交互机会:
- 输入
g,可以输入$E$上的点$P$,得到$f(P)$ - 输入
r,可以得到$E$上的随机点 - 输入
e,可以得到$GF(p)$下的$m \cdot x_G \cdot y_H$,其中$m$是flag对应的整数值
思路
既然可以随便拿$E$上的点,那么恢复曲线方程是不成问题的,而要解得flag就是要把$G,H$求出来,为此要想办法利用g。
而我的思路很简单,只要找$E$上的低阶点作为$P$,那么当$x_GP = O$时,$f(P)= x_PG + y_PH$,此时搜集两个方程就可以解出$G,H$来。
或者也可以构造$P$和$-P$发过去,总之能消掉$P$就可以了
exp
1 | from Crypto.Util.number import * |
Nahan(8 solves , 316 pts)
题目
题目描述:
1 | Nahan hides better than a cat at bath time; do the right thing at the right moment, and it pops out with the flag! |
题目:
1 | #!/usr/bin/env python3 |
题目首先生成比特长度为$l$的secret,记为$d$,并且给了其$\frac{l}{2}$次交互次数,每次交互内容为:
- 输入$s,t$,其比特长度$k$均需满足$83 < k < 124$
- 计算$(st) \oplus 2^l$,并取nextprime作为$r$,每次的$r$不能重复
- 给出$d \oplus r$的汉明重量
这里可以先测出来secret长度是248,交互次数是124
我们要在$\frac{l}{2}$次交互内恢复$d$,并提交给靶机得到flag。
思路
由于每次交互是给$d \oplus r$的汉明重量,并且$r$已知,因此我想到了SEETF的Neutrality这一题,也许能将0、1映射到1、-1然后LLL求解。但实际测试会发现,在这个问题下,方程仅有变量数的一半的时候恢复效果很一般,所以这个思路走不通。
测了一下如果再多30次左右交互,这种方法效果才好起来
而与Neutrality一题不同的点在于,这个题目的$r$并非完全随机,而是可以自己构造的,而@hashhash正好之前看过@Aqua Cat给他分享的一道算法题和这个有关:
https://www.luogu.com/article/1dzympve
@hashhash测试了一下,发现这个可以做到64次交互恢复192bit,而剩下的bit可以用多出来的很多交互次数一个个点就行,唯一的问题在于这64次发送的数据都必须是给定的,低位和高位可以有一些扰动。
想了一下这个还是可以做到,由于$r - \delta = (st) \oplus 2^l$,就有$(r - \delta) \oplus 2^l = st $,所以可以爆破$i$,尝试分解多个$(r+i) \oplus 2^l$,来得到满足要求的$s,t$即可。
因为低位可以扰动
我这题也就完成了这一小部分,给@hashhash打打杂把每一轮要输入的$s,t$给他,因为算法的部分看着比较头大(´・ω・`)
Tough Cookie
Silky(40 solves , 110 pts)
题目
题目描述:
1 | Silky’s ‘noisy’ equations are like static on a radio—annoying, but solvable if you tune just right. |
题目:
1 | #!/usr/bin/env sage |
题目流程为:
- 生成一个长为19的向量key,记为$\mathbf{k}$,其中每个分量均为$[-5,5]$中的随机整数
- 有最多10次交互机会,可以输入
m,拿到1088组silky(key) - 如果可以提交正确的$\mathbf{k}$,就可以拿到flag
其中,silky(key)生成的是满足如下两点要求长为19的向量$\mathbf{r}_i$:
- 所有分量均在$[-555, 555]$中随机取值
- $\mathbf{r}_i - \mathbf{k}$的每个分量需落在$[-550, 550]$中
思路
将$\mathbf{k}$的每个分量分开来看的话,10次交互机会等于是给了10880次关于该分量的不等式约束,比较简单的思路是对$[-5,5]$的整数逐个检验是否符合所有不等式约束即可。
exp
1 | from pwn import * |
Toffee(36 solves , 119 pts)
题目
题目描述:
1 | Sticky situation: Toffee’s crypto seems sweet, until you’re stuck chewing on its unsolvable core. |
题目:
1 | #!/usr/bin/env sage |
题目给定曲线$E$,随机生成三个数$u, v, k$,在此基础上进行ECDSA签名,每次签名的$k$会在模曲线阶$n$下线性递推,即$k_{i+1} = uk_i + v$。依然有无限次交互机会:
- 输入
g,可以再输入一个数$x$,返回$(ux+v) \% n$ - 输入
s,可以再输入一个消息,并得到对该消息的签名$(r,s)$
我们需要获得作为私钥的flag。
思路
思路实在太直白了,首先输入两次g把$u,v$拿到,之后再签名两次,利用线性$k$的关系式把$k$消掉就能拿到flag。
exp
1 | from Crypto.Util.number import * |
Lowdown(30 solves , 138 pts)
题目
题目描述:
1 | These 0s and 1s have the digital handwriting of a drunk Ph.D., trace their signature, sign your own name, and leak their crayon-scrawled Lowdown. |
题目:
1 | #!/usr/bin/env sage |
这个题看上去似乎比较麻烦,但是实际上并不是。总的来说题目基于一个奇怪的签名,我们可以获取任意长度小于10的消息签名值,要伪造一个长度为40的随机msg的签名,并且该签名对应的整数字符串前缀要满足分别为13和37,从而获得flag。其中签名的操作如下:
首先生成一组密钥$(g,g^{ar},r)$,其中$(g,g^{ar})$为公钥,$r$为私钥,$g$为$GF(2^8)$下的随机十阶可逆矩阵,$a,r$为$[2,2^{192}-2]$的随机值
对消息$m$,其签名值$s,t$满足:
其中$n$就是nonce,每次签名在$[2,2^{192}-2]$中随机取值
验签就验证$s\cdot t^{h(m)}$和$g^{ar}$相等即可,这很显然是成立的。
思路
再仔细看下他的验签函数:
1 | def verify(sgn, pkey, msg): |
可以看出这个验签函数实在过于简单了,没有对输入做任何可能的检查,因此伪造方式也非常容易,只需要先随意输入消息$m_1$,并获取到对他的签名$(s_1,t_1)$,此时就有:
直接随意选$t_2$,先使其满足前缀37的要求,然后计算:
然后令$s_2 = \frac{s_1}{k}$,多爆破几组使得其满足前缀13的要求就可以了。
公钥都不需要拿
这里有一个坑点在于他的msg本身就.encode()过,所以再从靶机发送过来会套两层b"",收到之后不能简单.decode()就结束。
exp
1 | from pwn import * |
Mechanic II(28 solves , 146 pts)
题目
题目描述:
1 | Mechanic II cranks PQC to hilarious levels, bring a quantum wrench and a PhD in pain. |
题目:
1 | #!/usr/bin/env python3 |
题目和前置题Mechanic一样,依然基于MLKEM_1024,只不过变成了交互题,看上去就长了很多。其流程为:
- 通过一个简单的哈希爆破pow
- 生成$n=1337$对密钥,并把私钥按顺序存放在列表
SKEYS里 - 生成$[0,1336]$的随机索引$r$,封装该密钥得到
cipher, shasec = kem.encaps(KEY_PAIR[r][0]) - 计算
secret = hashlib.sha3_256(shasec + hashlib.sha3_256(shasec + str(r).encode()).digest()).hexdigest()
我们有$3n+1$次交互机会:
- 输入
d,可以再输入一个ID,靶机用该位置的私钥对cipher解封装,并给出解封装得到的shasec - 输入
r,可以再输入一个ID,靶机将该位置的私钥的末32字节改成随机字节,并添加到列表SKEYS末尾 - 输入
s提交secret,正确就拿到flag
思路
由于交互部分能做的事情很有限,手动试一试就能试出来一个事实:对于正确的索引$r$来说,其私钥末32字节无论如何变动,解封装得到的shasec都是一样的,而索引错误时shasec则会变动,因此最坏的情况$3n$次交互也刚好可以获得正确的shasec和$r$了。
至于原理为什么是这样,问了一下Gemini说这似乎是Kyber的Key Mismatch Attack,但是具体是不是以及为什么是我就不太懂了,以后有机会再研究。
exp
1 | from pwn import * |
Mitram(24 solves , 164 pts)
题目
题目描述:
1 | Solving Mitram’s equations? Time to row reduce your expectations... and your sanity. |
题目:
1 | #!/usr/bin/env sage |
题目流程为:
在$GF(2^8)$下生成$m$个$(v+m,v+m)$的矩阵,存放在列表
F中生成一个$(v+m,v+m)$的$S$矩阵,其结构为:
其中子矩阵$S_{v, m}$的第一列嵌入了flag
计算公钥矩阵列表
P,其中每个矩阵结构满足:其中$G,H$都是列表
F中对应索引的矩阵的子矩阵,makeup是如下函数:1
2
3
4
5
6def makeup(M, n):
for i in range(n):
for j in range(i, n):
M[i, j] += M[j, i]
M[j, i] = 0
return M
给出F和P,要解出$S_{v, m}$,然后用其第一列的值还原flag。
思路
又是一个看上去有点复杂,但是实际上做法特别简单的题目,注意到公钥矩阵列表P中,每一个矩阵的右上角分块为:
而$G,H$都是可以从F中提取的,所以直接找$G+G^T$可逆的组,然后就可以直接解出$S_{v, m}$了。
exp
1 | dF = |
Asemoon(10 solves , 285 pts)
题目
题目描述:
1 | No entry until Asemoon’s token breaks! Can you reverse its secrets? |
题目:
1 | #!/usr/bin/env sage |
连接上靶机后,靶机先做下面的事情:
生成64bit的
skey,记为$s$,并随机生成一个度为64的不可约多项式$G$,记其整数值为CP定义一个
recheck函数,接受输入msg和v,实际上就是对msg做初始值为v的CRC64,所以后面直接把recheck直接记为CRC这里预计算的
CT应该就是为了加快计算
之后有无限次交互机会:
- 输入
l,可以再输入一个token,记其值为$v$,如果满足$CRC(s \oplus t, v) == v$,就能拿到flag,其中$t$是当前时间的整数值去掉个位,可以看作是已知的 - 输入
g,可以得到:- $y = CRC(m, CRC(s \oplus t, 0))$的值,其中
m = b"CCTF"是固定的 - 64bit的随机素数$p$以及$5^{CP} \% p$
- $y = CRC(m, CRC(s \oplus t, 0))$的值,其中
思路
首先要拿到CRC的模多项式$G$,也就是要拿到CP,这里不知道为什么不直接给,还要搞个花里胡哨的pub_2和pub_3出来,总之简单DLP一下就能拿到$G$。
拿到$G$之后,在模$G$的商环下,参考这篇能知道,题目的recheck(msg,v)可以写成如下等式:
其中$M$是输入msg对应的多项式,$I$是输入
v对应的多项式,$b$是8倍输入msg的字节长度
所以对于我们输入g拿到的值$y$对应的多项式$Y$,记$s \oplus t$对应的多项式为$M1$,m = b"CCTF"对应的多项式为$M_2$,有:
而我们需要的token对应的多项式$J$则满足:
因此利用$Y$将$M_1x^{64}$求出来即可求出$J$,转回整数再发送给靶机就能拿到flag。
exp
不知道为啥是概率成功的,CRC部分可能写的有点小bug:
1 | from Crypto.Util.number import * |
1 | from Crypto.Util.number import * |
Sobata II(8 solves , 316 pts)
题目
题目描述:
1 | Sobata_II is a hardened variant of Sobata, optimized for secure operations in large finite fields with enhanced resistance to attacks. |
题目:
1 | #!/usr/bin/env sage |
与前置题Sobata相比,基本函数是差不多的,几个小区别在于:
- 这题域换成了$GF(p^2)$,不过与之对应的$p$从512bit变成了196bit
jump函数中的模数从曲线阶变成了$GF(p^2)$的乘法群阶$p^2-1$
思路
这题最开始被@Q7用[sc for sc in g.__class__.__mro__[-1].__subclasses__() if sc.__name__ == 'catch_warnings'][0]()._module.__builtins__['__import__']('os').system('cat flag.py')直接RCE掉了XD,不过后来@factoreal似乎发现了端倪,修了这个让重做。
由于jump的阶压根不是曲线阶,所以没太好的办法让他像Sobata一样直接跳回来,但是由于$y^2= x^3 + d$这样的曲线在$GF(p^2)$下很容易是超奇异的,阶为$(p+1)^2$,所以就反复重连一直到这个光滑然后ECDLP就好了。
exp
这题偷懒就不写了吧:)
Juliax(7 solves , 334 pts)
题目
题目描述:
1 | Juliax’s partial RSA key is like a half-baked cookie crumbling, but still oddly satisfying to crack! |
题目:
1 | #!/usr/bin/env sage |
非常纯粹的题目,$d_p,d_q$均泄露了低512-313=199位,$e$为72位,要求分解$n$解RSA得到flag。
思路
可以说是见过不少次的论文了,直接抄个板子也能很快做出来,简单描述一下思路。
首先有:
得到:
未知的$d_{ph},d_{qh}$可以被模掉,也就是:
由于$e$只有72bit,那么$k,l$自然也很小,因此把两个等式稍作变形,把未知$p,q$合成已知的$n$,就能得到仅以$k,l$为小根的多项式:
然后二元copper就能解出来$k,l$。
之后再回看前面的等式,就比如选带$k$的等式:
这个等式在模$kp$下有一个313bit的小根$d_{ph}$,所以可以单元copper一下试试。
实际测的话sage自带的
small_roots应该打300bit就差不多了,还差13bit就只能爆一爆。差的这点上界可以照论文改shift多项式解决,当然最快的还是直接抄
exp
1 | from Crypto.Util.number import * |
1 | nbit, ebit, xbit = 512, 72, 313 |
Pearls(6 solves , 354 pts)
题目
题目描述:
1 | Unlock Pearls by hunting primes, each one brings you closer to the hidden flag! |
题目:
1 | #!/usr/bin/env python3 |
题目的encrypt看上去相当奇怪,不过先不管他,总的来说题目依然基于RSA分解$n$,为此提供了无限次交互:
输入
e,可以调用他的encrypt,对任意消息进行加密说实话没看出这有啥用,公钥都知道TT
输入
p,可以获得公钥$n$以及对flag使用encrypt加密的结果输入
b,可以输入次数$l$,从而获得burnish(skey, l)的结果,burnish(skey, l)函数内容为:1
2
3
4
5def burnish(skey, l):
nbit = skey[0].bit_length()
IRE = [[getRandomRange(0, 2), getRandomNBitInteger(nbit + getRandomRange(-3, 3)), getRandomNBitInteger(int(nbit * 0.74))] for _ in range(l)]
PLS = [skey[IRE[_][0]] * IRE[_][1] - IRE[_][2] for _ in range(l)]
return PLS
思路
encrypt虽然奇怪,但是仔细看下会发现,只要有私钥$p,q$,要反向写个decrypt是很容易的,因此重心是在分解$n$的步骤上,也就是如何利用b选项的输出。
而burnish函数其实也很明显是个AGCD问题,测试一下会发现五组就可以格出来。问题在于每一次的样本不仅可能是关于$p$的近似公约数,也可能是关于$q$的,所以还要多拿一些数据然后本地简单爆一下。
exp
1 | from Crypto.Util.number import * |
Goliver II(5 solves , 375 pts)
题目
题目描述:
1 | Goliver_II is an innovative elliptic curve cryptosystem designed to present unique challenges for the new era of cryptographic security. |
题目:
1 | #!/usr/bin/env python3 |
这个题目的前置题是昨年ASIS的这道Goliver,不过两者除了都使用Secp256k1以外没有什么相同之处,所以还是要理一下流程:
首先生成ECDSA的私钥$d$,以及公钥$dG$
每次连接靶机可以签三次名,签名式子看上去平平无奇:
不过对于题目来说有几个特色:
- 每次输入的不是要签名的
msg,而是输入一个整数sign_id,靶机会用这个计算$k_i = id + m$,其中$m$是flag的前半段对应的整数值 $h_i$永远不会变动,都是对flag的前半段的hash
签名仅返回$s_i$,不返回$r_i$
- 每次输入的不是要签名的
除了这个操作外,还可以做的交互有:
- 输入
v,可以验签 - 输入
g,可以提交私钥$d$,正确则拿到flag - 输入
p,可以拿到公钥$dG$
思路
一个非常大的问题在于,对于反复重连靶机,他只有私钥$d$会随着重连变动,而$k,r$这两个值只要输入的sign_id一样,就也会一直保持相同。
$h$更是永远都不会变
所以对于一次连接,多出来的变量仅有这次连接的私钥,但是却可以在这次连接中拿到三个等式,因此三次连接之后,我们就可以拿到大于变量数的等式。而由于方程中含有$r_id$这样的二次项,所以可以考虑用groebner解这个系统。
然后grorbner似乎不能直接解出来所有变量的值,加重连次数也没有太大作用。不过观察groebner出来的多项式结构可以发现有一个仅含$h$的二次多项式,所以可以求出其两个根再分别回代,就可以解出本次的$d$并提交了。
不能直接groebner出来的原因可能就是因为一定有多解
除此之外我还试了一下把所有等式乘$r_i^{-1}$,这样等式结构会变成:
这样做的好处在于,把$k_ir_i^{-1}$以及$hr_i^{-1}$看作新变量的话,这样的方程都是线性的,而线性系统求解显然比含二次项的多变量系统求解简单。
然而试了一下会发现矩阵的kernel总是有二维,所以多解确实是无论如何避免不了的
exp
1 | from Crypto.Util.number import * |
1 | from pwn import * |
1 | Vs = GF(o)["k, " + "h, " + "".join(["r"+str(i)+", " for i in range(3)]) + "".join(["d"+str(i)+", " for i in range(nums)])[:-2]] |
1 | PR.<x> = PolynomialRing(GF(o)) |
1 | k = o - 115792089237316195423570985008687907852837564279074780560359191442700976971211 |
Brain Buster
Phoney(25 solves , 159 pts)
题目
题目描述:
1 | Phoney laughs! Until you unpick its multi-prime RSA and random message lock. |
题目:
1 | #!/usr/bin/env python3 |
也是很直白的基于RSA的题目:
- $n = pqr$,三个因子分别是512,576,640bit
- 给出两个额外信息:
- $s = (p^{-1} \% qr) + p$
- $t = q \% p$
要求分解$n$来解RSA得到flag。
思路
首先,从$s$可以建出一个三次方程:
这个方程以$p$为根,而由于$p$在模$n$下很小所以可以copper出来。
直接
small_roots会返回0,把$x$换成$2x+1$即可,因为$p$的最低位一定是1
得到$p$之后可以把$q$写成$q = kp + t$,此时$k$只是一个64bit的小量,因此可以再copper一次拿到$q$。
exp
1 | from Crypto.Util.number import * |
Snails(14 solves , 236 pts)
题目
题目描述:
1 | Breaking Snails’ sigs? Even a decrypted flag moves at glacial pace! |
题目:
1 | #!/usr/bin/env sage |
题意非常简单,基于模数为521bit素数的ECDSA,私钥是flag,我们可以对任意长为40且包含特定子串的msg做ECDSA签名,要求还原私钥。
思路
题意简单,漏洞也十分明显,注意到每次$k$的比特长度和$h(m_i)$的比特长度一样,而hash用的是sha512,所以每次都相当于泄露了$k$的高9bit,因此当HNP问题做就可以拿到私钥。此外要是限制次数,还可以刻意选一些哈希值较小的msg发送过去签名,这样子泄露的比特更多。
这其实是昨年上半年的一个CVE(CVE-2024-31497),当时看到@石卡库写的公众号还去做了下φ(゜▽゜*)♪,不过这次既然可以用无限组那就偷懒不做消d、balance、BKZ之类的优化了,私钥长度也是随便弄的
exp
1 | p = 0x013835f64744f5f06c88c8d7ebfb55e127d790e5a7a58b7172f033db4afad4aca1ae1cdb891338cf963b30ff08d6af71327770d00c472c52290a60fb43f1d070025b |
Multi shooti(12 solves , 259 pts)
题目
题目描述:
1 | The Multi-shooti code left clues out in the open. Spot them, steal the key, grab the flag, and prove it’s not so tough after all. |
题目:
1 | #!/usr/bin/env python3 |
带S盒的题看着都头大,先放一下,以后再说(,,・ω・,,)
对称和流密码这种现在我已经退化成看到就直接润的程度了
Leptocole(2 solves , 450 pts)
题目
题目描述:
1 | Leptocole’s equation is so last-year, yet here you are, still solving for ‘U’ like a nerd! |
题目:
1 | #!/usr/bin/env sage |
这个是这次撑的最久的题目,到比赛结束两小时左右才被大伙搞定。虽然题目不太好做,但是题意反而很容易理解,其流程为(计算均定义在$GF(q)$下):
生成随机矩阵$G_{k,n}$
生成一个26x26的随机置换矩阵,并在置换矩阵每个非0位置乘上一个非零系数,得到矩阵$Q_{n,n}$
计算$GQ$的行阶梯形矩阵$H_{k, n}$,也就是存在可逆矩阵$K_{k,k}$使得$KGQ = H$
这个结构的$H$就很类似编码里生成矩阵的结构
然后就是交互部分:
输入
g,可以拿到$G$和$H$输入
s,可以逐行输入一个矩阵$U$和矩阵$P$,如果满足:- $UGP = H$
- $U$和$P$均可逆
就可以拿到flag。
思路
比较明显的是这是一个编码方向的问题,虽然我对编码了解的非常有限,不过队伍里@hashhash,@yolbby,@Aqua Cat和@Q7都懂编码,所以从大伙的对话我大概了解到这是一个码等价问题(Code Equivalence Problem),更具体的说,这是一个线性码等价问题(Linear Code Equivalence Problem),也就是题目标题的LEP。
这个等价很好理解,如果我们输入的$U = K$,$P=Q$的话,显然就满足题目要求,而如果能找到其他的输入也满足这个要求,那么$U,P$和$K,Q$在这个意义下就是等价的。
然而由于懂的实在太少,所以大伙最后集中讨论这题的时候我基本等于看天书,而且比赛第二天上午家里还有急事必须要走,就全靠队友carry(;´д`)ゞ。
不过@hashhash昨年的时候就预言了一波:前年CCTF有个同源的板子,昨年有个多变量的板子,那么今年说不定就有个编码的板子——事实证明确实如此,@Q7最后找到了针对这一道题目、并且还带有代码实现的这篇论文,能一定概率解决题目设置参数的码等价问题,然后@Aqua Cat超级快手秒写交互就出了。
仓库在这里
exp
1 | from ast import literal_eval |
1 | load("lep_solver.sage") |
1 | sh.recvuntil(b"[Q]uit") |
Head-Scratcher
Hoshi(6 solves , 354 pts)
题目
题目描述:
1 | Hoshi: a cryptic puzzle demanding brilliance, where only the sharpest minds unravel its celestial secrets. |
题目:
1 | #!/usr/bin/env sage |
这个题目题意也很简单,定义一条在$Zmod(p^{12})$下的曲线,给出上面的五个点$P_i$以及他们的倍点$Q_i=s_iP_i$,其中$s_i$均小于等于$p^{11}$,求解出所有的$s_i$并发回靶机就可以拿到flag。
思路
对于这种$Zmod(p^{k})$下的DLP问题,求解$Zmod(p^{k-1})$下的部分都是简单的,而对于ECDLP来说也就是Smart’s Attack,由于上次CodegateCTF正好写了一版,所以直接拿来用,却发现存在一个问题:对于$Zmod(p^4)$下能成功求解出来,但是$Zmod(p^5)$及以上就不行了。
问了一下Gemini说是精度问题,并且超过$p^4$的部分似乎需要迭代求解,让他写了个exp再稍微改了下发现确实就行了
赛后看discord的讨论发现$Zmod(p^4)$之后之所以不行似乎还有更深层次的原因:
exp
1 | def smarts_attack_dlog(P, Q, l): |
1 | from Crypto.Util.number import * |
1 | l, n = 12, 5 |
1 | sh.recvuntil(b"[Q]uit\n") |
1 | print(sh.recvline()) |
Alice Sig Slip(3 solves , 423 pts)
题目
题目描述:
1 | I messed up and a function wiped some of Alice's data. Can you help me restore it before she notices? |
题目:
1 | #!/usr/bin/env python3 |
这个题也是卡了大伙比较久。题目基于Ed25519的签名,流程为:
在连上靶机后,靶机生成密钥对,然后对下面五个消息进行签名:
1
2
3
4
5b"Alice cracks codes in her sleep."
b"Alice never leaves a cipher unsolved."
b"No flag for those who give up too soon, says Alice."
b"Alice never gives up; that's why she always gets the flag."
b"Alice loves solving ciphers, especially when they're tricky."签名值存放格式为
[public_key, r, s, msg]之后,靶机将五个消息的签名分别进行一定数量的”擦除”,然后发送给我们。也就是实际上我们拿到的五次消息对应的签名值为:
1
2
3
4
5[public_key, r, s, msg],
["", r, s, msg],
["", "", s, msg],
["", "", "", msg],
["", "", "", ""],我们需要往这些被擦除的签名里填入值,使得五个消息均通过Ed25519的验签就能拿到flag。
需要注意的是对签名值内已有的部分不能进行篡改
思路
前置知识
由于题目用的是库函数,没有把签名具体对应的等式写出来,所以这里先简单介绍一波。
首先,Ed25519并不是常见的Weierstrass型的椭圆曲线,而是一条扭曲爱德华曲线(Twisted Edwards Curve),照该曲线的常用记法:
- 记该曲线阶为$l$,基点为$B$,
- 我们的私钥为$k$,计算$\text{SHA512}(k)$,得到一个512bit的数字,记前半部分为$s$,后半部分为$t$
- 公钥为$A = sB$
那么对于该曲线上的签名,其式子为:
其中$r = h(t || M)$,此处注意签名值为$(R, S)$而非$(r,s)$。
验签即验证下式成立:
Standard curve database贴心的给全了Ed25519的参数以及其与Weierstrass型椭圆曲线的相互转换。
做法
回看一下我们实际拿到的五条内容:
1 | [public_key, r, s, msg], |
第一、第二、第四、第五条都没有问题:第一条压根不需要填,第二条填个public_key就行,第四、第五条自己生成个私钥去签名就可以了。因此关键在于第三条——我们需要在给定$S$的条件下,伪造出指定消息的一个签名,而可以操作的是公钥$A$以及$R$的值。
漏洞点在于Ed25519有一个8阶的子群,因此我们取该子群中的一点作为公钥$A$,那么验签的时候$8h(R || A || M)\cdot A$这一部分就消去了,剩下的就是$8S\cdot B = 8R$,此时用$R = S \cdot B$就可以通过验签了。
要注意一下解析数据时的大小端序
exp
1 | p = 0x7fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffed |
1 | def hex_to_E(hexdata): |
1 | from Crypto.PublicKey import ECC |
1 | while(1): |
SingleRow(3 solves , 423 pts)
题目
题目描述:
1 | SingleRow’s crypto is one line of defense, turns out it's also one line of nope! ;) |
题目:
1 | #!/usr/bin/env sage |
这个题基于UOV,梳理一遍题意头很大,不过好就好在可以站在巨人队友的肩膀上,换个角度理解这个题就简单很多。
思路
就我们的想法而言,整个题目浓缩一下其实就剩这样一小部分:
1 | from Crypto.Util.number import * |
核心点是这样:当flag当前bit为1时,输出的是一个$m \times (m+v)$的子空间中的向量,而当前bit为0时,直接不管他的sign具体是什么操作,总之输出的向量几乎不可能在这个子空间中。
而flag我们知道是以CCTF{}包裹住的,这就天然提供了24个1,因此在剩余的26个flag字符中,我们只需要找到17个1,和这24个1拼在一起,其矩阵的秩会是40而不是41,然后再将剩余向量挨个与这个矩阵拼起来检查秩即可逐bit做出判断。
@Q7给出了两个非常聪明的想法:
- 观察前面题目的flag,以
!}结尾的概率非常高 - 几乎每个flag都有好几个下划线,而下划线的二进制表示有足足六个1
因此爆下划线的位置是最方便的做法。
exp
1 | from itertools import combinations |
1 | flag_ = bytes_to_long(b"CCTF{" + b"\x00"*26 + b"}") |
1 | #################################################################################### check bit by bit |
其他
其实这个题在第一天晚上@hashhash就想出做法了,不过无论怎么调代码或者优化,flag就是出不来。
甚至@hashhash搞了一个究极优化的对1特别稀疏、没有下划线的flag都能秒出的做法,我们当时还醒着的几个全都本地生成数据测了一下,但对题目数据还是搞不出来flag,而且当时半夜四点多,@factoreal还要睡觉了:
于是我们产生了各种各样的怀疑:
附件数据放错了
redownload之后,附件数据还是放错了TT
flag不是以
CCTF开头的,也许是flag还猜过是
ASIS,毕竟昨年有个题目就是XD,不过试了下确实也不行
然后我想到了之前给SUCTF出题的时候利用了sage 10.5版本之后与更早的版本生成随机数的区别,但是没想到能怎么影响,不过还是简单提了一嘴,然后@Aqua Cat想到了一个问题:
但是@Aqua Cat测了下在9.5和10.4都测试了下发现@hashhash的做法都可以出,所以又感觉不是这个问题,问了下Gemini也说确实是这样:
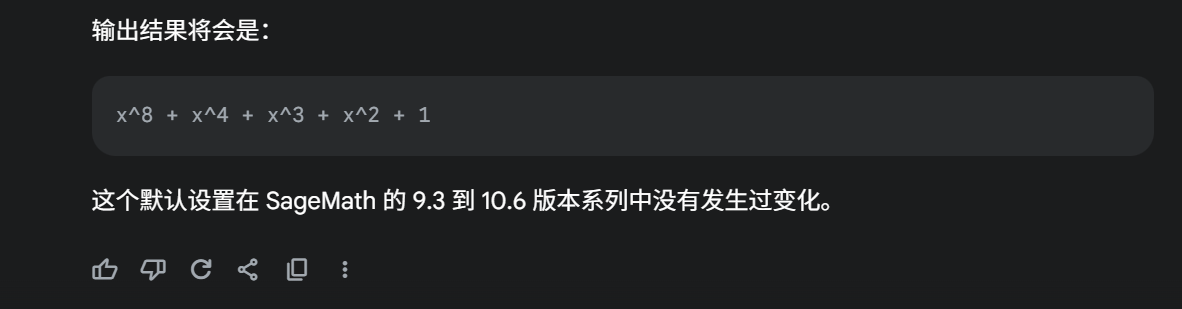
然而又过了一会儿@Aqua Cat把flag搞出来了,应该是爆破了模多项式,发现题目用的实际是:
然后赛后在discord上才看到@factoreal用的版本居然是:
好家伙,这确实太新了,要不是@hashhash弄了个几乎百分百本地能秒出的exp,还真难怀疑是这个问题。
很早很早很早之前,也就是昨年出NKCTF的这道题目的时候@rec和我提过这一点,说他很早之前也被sage不同版本的
modulus坑过,看来以后还要仔细留意下这个问题
总结
队友实在太强了,今年比赛对我来说真的算是混个老五冠军= ̄ω ̄=,赛后复现发觉审计代码的速度和写attack的速度还有很大进步空间,要慢慢努力了。
不过不管怎么说这次比赛结果很圆满,cyberCryer明年继续加油!
