2024-WMCTF-wp-crypto

写了一天的enigma还是没搞定，唉，古典！码力真的还是有点烂。

Matrix3是rec做的，不写在这篇，之后哪天有空把d3的两道matrix补上然后一起写一篇好了。

K-Cessation

题目描述：

K-Cessation
ChllengeInfo
misc/crypto 进入无界之界
## 背景：
K-Cessation 密码是一种使用 K 位轮从明文位中挑选下一个密文位的古典密码。
当加密开始时，从轮子的最后一位开始。
当轮子到达终点时，它会从头开始循环。
对于每个明文位，轮子会旋转到轮子中与明文位匹配的下一个位，并将旋转的距离附加到密文中。

因此，如果不知道轮子，就不可能解密密文。
是这样吗？


## 例子：
要使用轮子 1100011011100011100110100011110110010110010100001011111011111010 将“youtu.be/dQw4w9WgXcQ”编码为 64-Cessation：
1. 将明文转换为比特： 01111001 01101111 01110101 01110100 01110101 00101110 01100010 01100101 00101111 01100100 01010001 01110111 0011 0100 01110111 00111001 01010111 01100111 01011000 01100011 01010001
2.从wheel[-1]到轮子中的下一个“0”位，距离为3，当前轮位置为wheel[2]
3.从wheel[2]到轮子中的下一个“1”位，距离为3，当前轮子位置为wheel[5]
4. 重复步骤直到所有位都被编码
5.结果为3312121232111411211311221152515233123332223411313221112161142123243321244111111311111112111131113211132412111212112112321122115251142114213312132313311222111112


## 挑战：
一个野生Flag使用 64-Cessation 密码进行编码。
轮子内容是未知的，它是 64 位长。
密文在 ciphertext.txt 中给出。
该Flag已知是长度超过 64 个字符的 ASCII 字符串。
除此之外，该Flag的任何部分都是未知的，这意味着该Flag不是 WMCTF{} 或 FLAG{} 格式。
提交时，请将Flag改为WMCTF{}格式。
请注意，每个ASCII字节的最高有效位被随机翻转。
您需要从密文中提取Flag并提交。
为了您的方便，flag_hash.txt 中给出了该Flag的盐焗 SHA-256 哈希值。

ChllengeInfo-EN
misc/crypto Enter the realm of no realm
## Background:
K-Cessation cipher is a cipher that uses a K bit wheel to pick the next cipher bit from plaintext bit.
When encryption starts, the wheel starts at the last bit of the wheel.
The wheel loops around when it reaches the end.
For every plaintext bit, the wheel is rotated to the next bit in the wheel that matches the plaintext bit, and the distance rotated is appended to the ciphertext.

Therefore, if the wheel is not known, it is not possible to decrypt the ciphertext.
Or is it?


## Example:
To encode "youtu.be/dQw4w9WgXcQ" in 64-Cessation with the wheel 1100011011100011100110100011110110010110010100001011111011111010:
1. convert the plaintext to bits: 01111001 01101111 01110101 01110100 01110101 00101110 01100010 01100101 00101111 01100100 01010001 01110111 00110100 01110111 00111001 01010111 01100111 01011000 01100011 01010001
2. from wheel[-1] to the next "0" bit in the wheel, distance is 3, the current wheel position is wheel[2]
3. from wheel[2] to the next "1" bit in the wheel, distance is 3, the current wheel position is wheel[5]
4. repeat the steps until all bits is encoded
5. the result is 3312121232111411211311221152515233123332223411313221112161142123243321244111111311111112111131113211132412111212112112321122115251142114213312132313311222111112


## Challenge:
A flag is encoded with 64-Cessation cipher.
The wheel is not known except that it is 64 bits long.
The ciphertext is given in ciphertext.txt.
The flag is only known to be an ASCII string that is longer than 64 characters.
No part of the flag is known, which means the flag is NOT in WMCTF{} or FLAG{} format.
When submitting, please make the flag in WMCTF{} format.
Note that, The most significant bit of each ASCII byte is flipped with a random bit.
You need to extract the flag from the ciphertext and submit it.
For your convenience, a salted sha256 hash of the flag is given in flag_hash.txt.

题目：

from typing import List,Union,Literal
from Crypto.Util.number import long_to_bytes
import secrets
import random,string,re

class K_Cessation:
    '''
    ## Background:
    K-Cessation cipher is a cipher that uses a K bit wheel to pick the next cipher bit from plaintext bit.
    When encryption starts, the wheel starts at the last bit of the wheel.
    The wheel loops around when it reaches the end.
    For every plaintext bit, the wheel is rotated to the next bit in the wheel that matches the plaintext bit, and the distance rotated is appended to the ciphertext.

    Therefore, if the wheel is not known, it is not possible to decrypt the ciphertext. 
    Or is it?

    
    ## Example:
    To encode "youtu.be/dQw4w9WgXcQ" in 64-Cessation with the wheel 1100011011100011100110100011110110010110010100001011111011111010:
    1. convert the plaintext to bits: 01111001 01101111 01110101 01110100 01110101 00101110 01100010 01100101 00101111 01100100 01010001 01110111 00110100 01110111 00111001 01010111 01100111 01011000 01100011 01010001
    2. from wheel[-1] to the next "0" bit in the wheel, distance is 3, the current wheel position is wheel[2]
    3. from wheel[2] to the next "1" bit in the wheel, distance is 3, the current wheel position is wheel[5]
    4. repeat the steps until all bits is encoded
    5. the result is 3312121232111411211311221152515233123332223411313221112161142123243321244111111311111112111131113211132412111212112112321122115251142114213312132313311222111112


    ## Challenge:
    A flag is encoded with 64-Cessation cipher. 
    The wheel is not known. 
    The ciphertext is given in ciphertext.txt.
    The flag is only known to be an ascii string that is longer than 64 characters. 
    No part of the flag is known, which means the flag is NOT in WMCTF{} or FLAG{} format.
    When submitting, please make the flag in WMCTF{} format.
    The most significant bit of each byte is flipped with a random bit.
    You need to extract the flag from the ciphertext and submit it.
    For your convenience, a salted sha256 hash of the flag is given in flag_hash.txt.

    '''

    def __is_valid_wheel(self):
        hasZero = False
        hasOne = False
        for i in self.wheel:
            if not isinstance(i,int):
                raise ValueError("Wheel must be a list of int")
            if i == 0:
                hasZero = True
            elif i == 1:
                hasOne = True
            if i > 1 or i < 0:
                raise ValueError("Wheel must be a list of 0s and 1s")
        if not hasZero or not hasOne:
            raise ValueError("Wheel must contain at least one 0 and one 1")

    def __init__(self,wheel:List[int]):
        self.wheel = wheel
        self.__is_valid_wheel()
        self.state = -1
        self.finalized = False
    def __find_next_in_wheel(self,target:Literal[1,0]) -> List[int]:
        result = 1
        while True:
            ptr = self.state + result
            ptr = ptr % len(self.wheel)
            v = self.wheel[ptr]
            if v == target:
                self.state = ptr
                return [result]
            result+=1
    def __iter_bits(self,data:bytes):
        for b in data:
            for i in range(7,-1,-1):
                yield (b >> i) & 1
    def __check_finalized(self):
        if self.finalized:
            raise ValueError("This instance has already been finalized")
        self.finalized = True
    def encrypt(self,data:Union[str,bytes]) -> List[int]:
        self.__check_finalized()
        if isinstance(data,str):
            data = data.encode()
        out = []
        for bit in self.__iter_bits(data):
            rs = self.__find_next_in_wheel(bit)
            # print(f"bit={bit},rs={rs},state={self.state}")
            out.extend(rs)
        return out
    
    def decrypt(self,data:List[int]) -> bytes:
        self.__check_finalized()
        out = []
        for i in data:
            assert type(i) == int
            self.state = self.state + i
            self.state %= len(self.wheel)
            out.append(self.wheel[self.state])
        long = "".join(map(str,out))
        return long_to_bytes(int(long,2))

# generate a random wheel with k bits.
def random_wheel(k=64) -> List[int]:
    return [secrets.randbelow(2) for _ in range(k)]

# the most significant bit of each byte is flipped with a random bit.
def encode_ascii_with_random_msb(data:bytes) -> bytes:
    out = bytearray()
    for b in data:
        assert b < 128, "not ascii"
        b = b ^ (0b10000000 * secrets.randbelow(2))
        out.append(b)
    return bytes(out)

# for your convenience, here is the decoding function.
def decode_ascii_with_random_msb(data:bytes) -> bytes:
    out = bytearray()
    for b in data:
        b = b & 0b01111111
        out.append(b)
    return bytes(out)


if __name__ == "__main__":
    try:
        from flag import flag
        from flag import wheel
    except ImportError:
        print("flag.py not found, using test flag")
        flag = "THIS_IS_TEST_FLAG_WHEN_YOU_HEAR_THE_BUZZER_LOOK_AT_THE_FLAG_BEEEP"
        wheel = random_wheel(64)

    # wheel is wheel and 64 bits
    assert type(wheel) == list and len(wheel) == 64 and all((i in [0,1] for i in wheel))
    # flag is flag and string
    assert type(flag) == str
    # flag is ascii
    assert all((ord(c) < 128 for c in flag))
    # flag is long
    assert len(flag) > 64
    # flag does not start with wmctf{ nor does it end with }
    assert not flag.lower().startswith("wmctf{") and not flag.endswith("}")
    # flag also does not start with flag{
    assert not flag.lower().startswith("flag{")

    # the most significant bit of each byte is flipped with a random bit.
    plaintext = encode_ascii_with_random_msb(flag.encode())

    c = K_Cessation(wheel)
    ct = c.encrypt(plaintext)
    with open("ciphertext.txt","w") as f:
        f.write(str(ct))

    import hashlib
    # for you can verify the correctness of your decryption.
    # or you can brute force the flag hash, it is just a >64 length string :)
    with open("flag_hash.txt","w") as f:
        salt = secrets.token_bytes(16).hex()
        h = hashlib.sha256((salt + flag).encode()).hexdigest()
        f.write(h + ":" + salt)

    # demostration that decryption works
    c = K_Cessation(wheel)
    pt = c.decrypt(ct)
    pt = decode_ascii_with_random_msb(pt)
    print(pt)
    assert flag.encode() in pt

ciphertext.txt：

[2, 1, 1, 3, 1, 1, 3, 2, 1, 4, 1, 2, 3, 1, 1, 1, 2, 1, 1, 2, 2, 2, 1, 3, 1, 6, 1, 1, 4, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 1, 1, 3, 3, 2, 1, 1, 3, 1, 1, 1, 3, 4, 1, 3, 1, 2, 2, 4, 2, 5, 1, 1, 1, 3, 2, 1, 4, 2, 2, 1, 2, 1, 3, 1, 1, 1, 1, 1, 2, 3, 1, 2, 1, 1, 1, 1, 3, 4, 1, 2, 2, 4, 2, 5, 1, 2, 1, 2, 2, 1, 4, 1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 2, 2, 1, 4, 3, 1, 2, 1, 3, 1, 3, 3, 2, 1, 3, 1, 6, 2, 1, 1, 2, 1, 2, 1, 3, 1, 1, 2, 1, 2, 1, 1, 2, 1, 2, 2, 2, 3, 1, 1, 4, 1, 3, 1, 1, 1, 2, 1, 1, 2, 4, 1, 1, 5, 2, 4, 2, 2, 1, 1, 1, 2, 1, 1, 1, 2, 1, 3, 3, 1, 1, 1, 1, 1, 2, 1, 2, 3, 1, 1, 2, 1, 1, 2, 1, 2, 1, 2, 1, 1, 1, 2, 5, 1, 1, 1, 3, 1, 1, 2, 3, 1, 2, 2, 2, 1, 3, 3, 1, 1, 2, 1, 1, 4, 3, 1, 3, 4, 1, 1, 1, 2, 1, 3, 1, 6, 1, 2, 1, 1, 3, 2, 3, 1, 2, 2, 1, 3, 2, 1, 2, 2, 2, 3, 3, 3, 1, 1, 2, 4, 1, 1, 1, 1, 1, 4, 2, 1, 4, 1, 2, 3, 2, 1, 1, 1, 2, 1, 1, 1, 2, 1, 3, 2, 1, 2, 1, 1, 1, 4, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 2, 4, 2, 1, 4, 2, 4, 2, 2, 3, 1, 2, 2, 2, 1, 3, 3, 1, 2, 1, 1, 1, 1, 3, 3, 1, 3, 1, 1, 1, 1, 3, 1, 1, 4, 2, 5, 2, 1, 3, 1, 1, 2, 3, 1, 2, 2, 1, 1, 1, 1, 1, 1, 3, 1, 2, 1, 3, 1, 2, 3, 4, 4, 3, 2, 4, 2, 1, 4, 2, 4, 1, 2, 1, 3, 1, 2, 1, 1, 1, 3, 2, 1, 2, 2, 2, 3, 3, 1, 2, 1, 3, 1, 1, 1, 2, 1, 3, 4, 2, 1, 4, 1, 2, 1, 2, 2, 2, 1, 1, 2, 1, 1, 2, 2, 2, 1, 4, 2, 1, 4, 1, 1, 1, 1, 2, 4, 4, 3, 2, 4, 2, 1, 1, 1, 1, 1, 1, 1, 4, 2, 2, 3, 1, 1, 1, 2, 1, 3, 1, 4, 1, 2, 4, 1, 2, 3, 4, 1, 3, 1, 1, 1, 2, 4, 1, 1, 1, 4, 1, 1, 4, 2, 1, 4, 2, 2, 1, 1, 1, 1, 1, 2, 3, 2, 1, 4, 3, 3, 4, 4, 3, 2, 4, 2, 1, 1, 3, 2, 4, 1, 1, 2, 3, 1, 1, 1, 2, 2, 1, 1, 1, 1, 3, 1, 1, 1, 4, 3, 3, 1, 1, 2, 1, 1, 1, 1, 3, 1, 1, 4, 2, 5, 1, 1, 4, 2, 1, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 2, 1, 2, 1, 2, 4, 3, 1, 1, 1, 1, 3, 4, 3, 1, 1, 4, 1, 6, 2, 1, 1, 1, 3, 1, 1, 3, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 4, 3, 1, 1, 5, 4, 1, 2, 2, 4, 1, 6, 1, 2, 1, 1, 3, 1, 4, 1, 2, 1, 2, 1, 1, 1, 1, 4, 2, 2, 3, 1, 2, 3, 1, 3, 4, 1, 1, 3, 4, 2, 5, 1, 1, 1, 3, 2, 2, 3, 2, 1, 2, 2, 2, 2, 3, 1, 2, 1, 3, 3, 3, 1, 1, 2, 1, 3, 3, 1, 1, 4, 2, 5, 2, 4, 1, 2, 4, 1, 2, 1, 2, 1, 1, 1, 2, 3, 1, 2, 4, 1, 1, 4, 4, 1, 1, 2, 3, 2, 4, 2, 5, 1, 2, 1, 2, 1, 1, 2, 3, 1, 2, 1, 2, 1, 1, 3, 1, 1, 2, 1, 2, 3, 1, 1, 1, 3, 4, 1, 1, 2, 1, 1, 1, 2, 4, 2, 1, 1, 3, 1, 2, 1, 2, 2, 2, 1, 2, 2, 1, 1, 1, 2, 1, 3, 1, 1, 2, 1, 2, 3, 1, 1, 1, 3, 4, 1, 1, 2, 3, 1, 2, 3, 1, 6, 2, 1, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 1, 1, 1, 4, 2, 1, 4, 1, 2, 3, 1, 1, 2, 1]

flaghash.txt：

1	d650078ae91d82ebd1d586110960a789c1a15e2cbc053b9daf8d8a4905950720:b840089ce93581869e9c02a7b5aefa7b

题目基于一个特殊的加密方式：

初始化一个随机的长度为64的比特串wheel，并置初始指针为-1
把flag转为二进制串，并将他的MSB做随机处理
按flag比特进行加密。比如第一比特是0，那么指针向右循环移动至wheel下一个0的位置，并记录本次移动距离；第二比特为1，那么指针向右循环移动至wheel下一个1的位置，并记录本次移动距离。如此重复直到加密完所有比特
给出所有移动距离，要求还原明文

可以看出，如果能恢复完整的wheel，就可以直接用作为密文的距离恢复flag的各个bit。而如果MSB没有处理的话，我们就拥有了wheel中64个一定为0的位置(这些位置会产生重复)，那么就对我们恢复wheel有很大帮助了。

然而问题就在于MSB有随机处理过，所以对于flag串我们可以说几乎是一无所知，因此要想别的办法。

而注意到以下几个事实：

如果当前记录的距离为1，则本次移动涉及两个连续比特，没法得知这两个比特任意一个的信息
如果当前记录的距离为2，则本次移动涉及3个连续比特，可以知道的事实是：第二比特和第三比特一定不同
如果当前记录的距离为n，则本次移动涉及(n+1)个连续比特，可以知道的事实是：第2-n个比特一定相同，且一定和第n+1个比特不同

而我们有足够多的密文，因此我们可以通过这样的关系，确定很多一定相同或一定不同的比特，也就是把所有比特分为两类。这个时候假设其中某一类比特是0，另一部分就是1，就得到了可能的wheel，然后结合flaghash对所有可能的wheel进行爆破就可以了。

exp：

from Crypto.Util.number import *
import hashlib

c = [2, 1, 1, 3, 1, 1, 3, 2, 1, 4, 1, 2, 3, 1, 1, 1, 2, 1, 1, 2, 2, 2, 1, 3, 1, 6, 1, 1, 4, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 1, 1, 3, 3, 2, 1, 1, 3, 1, 1, 1, 3, 4, 1, 3, 1, 2, 2, 4, 2, 5, 1, 1, 1, 3, 2, 1, 4, 2, 2, 1, 2, 1, 3, 1, 1, 1, 1, 1, 2, 3, 1, 2, 1, 1, 1, 1, 3, 4, 1, 2, 2, 4, 2, 5, 1, 2, 1, 2, 2, 1, 4, 1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 2, 2, 1, 4, 3, 1, 2, 1, 3, 1, 3, 3, 2, 1, 3, 1, 6, 2, 1, 1, 2, 1, 2, 1, 3, 1, 1, 2, 1, 2, 1, 1, 2, 1, 2, 2, 2, 3, 1, 1, 4, 1, 3, 1, 1, 1, 2, 1, 1, 2, 4, 1, 1, 5, 2, 4, 2, 2, 1, 1, 1, 2, 1, 1, 1, 2, 1, 3, 3, 1, 1, 1, 1, 1, 2, 1, 2, 3, 1, 1, 2, 1, 1, 2, 1, 2, 1, 2, 1, 1, 1, 2, 5, 1, 1, 1, 3, 1, 1, 2, 3, 1, 2, 2, 2, 1, 3, 3, 1, 1, 2, 1, 1, 4, 3, 1, 3, 4, 1, 1, 1, 2, 1, 3, 1, 6, 1, 2, 1, 1, 3, 2, 3, 1, 2, 2, 1, 3, 2, 1, 2, 2, 2, 3, 3, 3, 1, 1, 2, 4, 1, 1, 1, 1, 1, 4, 2, 1, 4, 1, 2, 3, 2, 1, 1, 1, 2, 1, 1, 1, 2, 1, 3, 2, 1, 2, 1, 1, 1, 4, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 2, 4, 2, 1, 4, 2, 4, 2, 2, 3, 1, 2, 2, 2, 1, 3, 3, 1, 2, 1, 1, 1, 1, 3, 3, 1, 3, 1, 1, 1, 1, 3, 1, 1, 4, 2, 5, 2, 1, 3, 1, 1, 2, 3, 1, 2, 2, 1, 1, 1, 1, 1, 1, 3, 1, 2, 1, 3, 1, 2, 3, 4, 4, 3, 2, 4, 2, 1, 4, 2, 4, 1, 2, 1, 3, 1, 2, 1, 1, 1, 3, 2, 1, 2, 2, 2, 3, 3, 1, 2, 1, 3, 1, 1, 1, 2, 1, 3, 4, 2, 1, 4, 1, 2, 1, 2, 2, 2, 1, 1, 2, 1, 1, 2, 2, 2, 1, 4, 2, 1, 4, 1, 1, 1, 1, 2, 4, 4, 3, 2, 4, 2, 1, 1, 1, 1, 1, 1, 1, 4, 2, 2, 3, 1, 1, 1, 2, 1, 3, 1, 4, 1, 2, 4, 1, 2, 3, 4, 1, 3, 1, 1, 1, 2, 4, 1, 1, 1, 4, 1, 1, 4, 2, 1, 4, 2, 2, 1, 1, 1, 1, 1, 2, 3, 2, 1, 4, 3, 3, 4, 4, 3, 2, 4, 2, 1, 1, 3, 2, 4, 1, 1, 2, 3, 1, 1, 1, 2, 2, 1, 1, 1, 1, 3, 1, 1, 1, 4, 3, 3, 1, 1, 2, 1, 1, 1, 1, 3, 1, 1, 4, 2, 5, 1, 1, 4, 2, 1, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 2, 1, 2, 1, 2, 4, 3, 1, 1, 1, 1, 3, 4, 3, 1, 1, 4, 1, 6, 2, 1, 1, 1, 3, 1, 1, 3, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 4, 3, 1, 1, 5, 4, 1, 2, 2, 4, 1, 6, 1, 2, 1, 1, 3, 1, 4, 1, 2, 1, 2, 1, 1, 1, 1, 4, 2, 2, 3, 1, 2, 3, 1, 3, 4, 1, 1, 3, 4, 2, 5, 1, 1, 1, 3, 2, 2, 3, 2, 1, 2, 2, 2, 2, 3, 1, 2, 1, 3, 3, 3, 1, 1, 2, 1, 3, 3, 1, 1, 4, 2, 5, 2, 4, 1, 2, 4, 1, 2, 1, 2, 1, 1, 1, 2, 3, 1, 2, 4, 1, 1, 4, 4, 1, 1, 2, 3, 2, 4, 2, 5, 1, 2, 1, 2, 1, 1, 2, 3, 1, 2, 1, 2, 1, 1, 3, 1, 1, 2, 1, 2, 3, 1, 1, 1, 3, 4, 1, 1, 2, 1, 1, 1, 2, 4, 2, 1, 1, 3, 1, 2, 1, 2, 2, 2, 1, 2, 2, 1, 1, 1, 2, 1, 3, 1, 1, 2, 1, 2, 3, 1, 1, 1, 3, 4, 1, 1, 2, 3, 1, 2, 3, 1, 6, 2, 1, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 1, 1, 1, 4, 2, 1, 4, 1, 2, 3, 1, 1, 2, 1]
flag_hash = "d650078ae91d82ebd1d586110960a789c1a15e2cbc053b9daf8d8a4905950720"
salt = b"b840089ce93581869e9c02a7b5aefa7b"

########################################################################### part1 find same and diff
same_set = []
diff_set = []
idx = -1
for i in range(len(c)):
    if(c[i] == 2):
        diff_set.append(str([(idx + c[i] - 1) % 64, (idx + c[i]) % 64]))
    elif(c[i] > 2):
        temp = []
        for j in range(1,c[i]):
            temp.append((idx+j)%64)
        same_set.append(str(temp))
        diff_set.append(str([(idx + c[i] - 1) % 64, (idx + c[i]) % 64]))
    idx = (idx + c[i]) % 64

same_set = sorted(list(map(eval,set(same_set))))
diff_set = sorted(list(map(eval,set(diff_set))))

########################################################################### part2 find wheel(by hand)
WHEEL = ["*" for i in range(64)]

for brute in range(8):
    wheel = WHEEL
    temp = bin(brute)[2:].zfill(3)
    wheel[0] = int(temp[0])
    wheel[42] = int(temp[1])
    wheel[49] = int(temp[2])
    for i in range(64):
        if([i,i+1] in diff_set and wheel[i] != "*"):
            wheel[i+1] = 1 - wheel[i]
        for j in range(10):
            if([i+t for t in range(j)] in same_set and wheel[i] != "*"):
                for t in range(j):
                    wheel[i+t] = wheel[i]
    
    flag = ""
    idx = -1
    for i in range(len(c)):
        idx = (idx+c[i]) % 64
        if(i % 8 == 0):
            flag += "0"
        else:
            flag += str(wheel[idx])
    FLAG = long_to_bytes(int(flag,2))

    h = hashlib.sha256(salt + FLAG).hexdigest()
    if(h == flag_hash):
        print(FLAG)


#DoubleUmCtF[S33K1NG_tru7h-7h3_w1s3-f1nd_1n57e4d-17s_pr0f0und-4b5ence_n0w-g0_s0lv3-th3_3y3s-1n_N0ita]

FACRT

题目描述：

1	ERROR ERROR ERROR, please replace flag{} to WMCTF{}

题目：

import gmpy2
from secret import flag
from Crypto.Util.number import *
Count=20
p=getPrime(512)
q=getPrime(512)
e=65537
n=p*q
d=gmpy2.invert(e,(p-1)*(q-1))
dp=d%(p-1)
dq=d%(q-1)
print(f"n={n}")
flag=bytes_to_long(flag)
length=flag.bit_length()
print(f"length={length}")
m=[]
for i in range(Count):
    m.append(getPrime(length))
sq=[]
sq_=[]
sp=[]
for i in range(Count):
    sq.append(pow(m[i],dq,q))
    sq_.append(int('0'*32+bin(pow(m[i],dq,q))[2:][32:],2))
    sp.append(pow(m[i], dp, p))
for i in range(Count):
    assert sq_[i] < q / 32
iq=inverse(q,p)
s=[]
for i in range(Count):
    s.append(int(sq_[i]+q*(((sp[i]-sq[i])*iq)%p)))
print(f"s={s}")
print(f"c={pow(flag,e,n)}")
'''
n=147633197136297320644148532167800594954463904917041365729781214689541810163409922050566363432759473356227399211204573839844534932354354132513677032099679754947582227369942835464578888307376910610182166537589845612944804885745392209830996561055058293663757559573736079810999615542354866920007861214183738025983
length=455
s=[135516280150137458535561766358086896198348823398876741567317041366935426854394060237235814065881756890818477438426875999503748746848408802883160976139168309216479723387043154316328752466115337006276833313025698482591954333004698732007362032602920842020200559463427548622804767419825141012760232500564198606888, 87138950331850035073233755923193357352015776817591237970872234630746818824503152055070348052111940612563932340910671611099400897135890145261451245577578879099083666861166614841834235097485990689182812564858373409987914436273165881047892580175317423057893816031028632720419872660582122916390309733324086153485, 138644295462947977586933469377687701489914340911921767410183452121042506019270712424245627451242649429408423057598802920666169608453899414528460692023716837136269325732757807484480055069814533664161537001762727348850128480964361110794017997076616622537153343830644577017008185863066319652708947485342513469942, 130919765117872700420555258668777170220585743300145967201676029268553369762501611700891574139388115937578229121079450407536963982339229719500478504489500235690293048515731859346431065030206394207045994366861194654126521065191859763903957682731311119322278004810859526215299984270862147897660764896871931296525, 114700370393183453087762195804219894122789831440066263230660331964018561704119945094712846882622289910478787117536755419287483635582978440493028286129198190921201156025431173751752743507530849046089710840106416071119787801330709608148349917138686962228418379795866832374558526179470426187199100866047189895398, 5526726757049511570122924251009639296817346269475117861098612689025237993752241296662636520025051472762072465223105287132204748691454643208692589407448303681720594661639751550346640974853714675951318971703834962983574657923366839131735681149307918005820142824780727533061358686675519367812942183782965460156, 144912005915009185433389709621768898379612902758176190094171990137016617813547436225820194585543950753591409962313416349983080186189291716456666174265994068233652987757656436662736504159419091874803636330149391525094620604417895137599924048423029008070688563937967247938795175561463188529887593887274447829757, 136250954616195732816473240575012270303125387854617764474032021538389021573726037002975200362404464882071072085887627232185387656472286476406393582907753248439212389626213347657516288312775908225085848334636924022113242155272938168661245231559256589332709251562390352253724058379737367174585436687621017694623, 62581851774850409035755528242738381905999051352008432547471965980273593728343556710086776830920012955472867109461528976241913935857428013748626805913556479910568244555311572298067590116614399220857206962127377751825672045446525674748896825242976163703599291103837976885179955618472741727241520609778322846005, 145854407984474847551927547284413490204495969306617565827750995876170774717809213321826036612782367152524129825636642176629348378245478404356883485091652713207020554564450132585121134356935492165152072283066165961023761302228624528890490009909363984222514631061033009247208437816124596049012309910840440309561, 124551623006909497965848991707513696948607938882176233365140848984406516643540438381538258922460588883294565931391660391812373244670311091543926813390568684148523894758100116918211999135492588543339785067482674405654655248001114133508625872962520401753384795662160688811171758878041475228921004115541651588149, 15938340419155549703292732921378484283671988749432038679365417994992859057494159116052524559743521485794692543381549875094855921795753932087886980295291140542937847588182771711846510176440458231173636452634043298156122152860644504752015830250690063832495966826188439527832958662817314634043438801092078111173, 86793422805279107846504839960808639992922541788273836408000957039906527697664805903722395255793430323591730573513732464380853123117859130756589515125491536316134863620706530836481623063642225089209431819777355554001327119466306759145993282751212553582691384017307673738794439532271560215747589628721710135897, 108675608374666743358023889479027512878400550037574532652565479774965642002565282273742545254311704772402696446846722391711332035309818100961301897022556307435354059324998874351394451945385491984524729822436607930537193897390621277431306545936473390631504396022406944910561421866589605078829721977335264154976, 87317748227288225233288224866786892964848811364878121564104341670954340348393418506174791619641614941888448848731903276361744955803183864888079233767189621441829023235771802783069311610169253651371628757455646066049167648114996530344278325612462268009587440597096690136975144034630898406289420602499264991623, 56652314874573546743584841968373113846850609963672297223607913939552862285375621862172324584570593402935091802803893885963277174956979046479939956703429737288793705461324779449285529662821030340203158503181009684937887687542388010343147675680002397630598445715400876202643169104742361423214638787268742234287, 98735788313453186782519834728824046613708479524564270665693218086798600541964070362862728960696910092702768075145925801913657156092005722008779014906938783990621453314812381950847944890837178907520481282447677162465215252648603374266972153988621533116563623242402366677831684416116807732808111964626488086987, 127540651954215161413641876933455408716614015796900097859173650400979733321781230732298931541274922911072112231027539634566966261240603321076224739659191443221985808678247919491141075440774231707687287562522535460013252508304387645505398442899700006526196099765002065480554613895222880144277349674640005507562, 133301958266564440496259158450519409455902192149222024966338884662576908051145274628854034018802181764563054480089111531034013218222971811942750317186820576575720998626362983321816936975595432624528396429872313110972358282919447478636004224335379606216720361742943716434992065840043748957089654449955193986860, 88160039502967812710045720428993741346375421128152598672398002732708719698481663322248764249302216242451840620334870977104442381110519298390156672581547539043729567682679341598750864890008905914145991583715826910836568061276943119691386206504777140515604809396852491015959654881350560399518061528959314304087]
c=123907837039511977819816858353976764990739800475355111239750335121820426041872830656170595604631534502233882297517774737660499087852687022473212169680375890135271089504199640532421067201796868951827680690124297723304485612987566782809086630400500307531954278635605686302923551049889311808990254356288059153559
'''

题目基于RSA的CRT，但是由于把$m^{d_q}$那部分的高位进行了处理，所以得到的最终结果并不是$m^d$。

而由CRT的式子有：

$s_i = qt_i + (m_i^{d_q})_{lsb}$

写成这个形式可以发现后面那一部分相对较小，所以其实就变成了一个AGCD问题：

$s_i = qt_i + r_i$

因此格一格就好。

exp：

from Crypto.Util.number import *

Count = 20
e = 65537
n = 147633197136297320644148532167800594954463904917041365729781214689541810163409922050566363432759473356227399211204573839844534932354354132513677032099679754947582227369942835464578888307376910610182166537589845612944804885745392209830996561055058293663757559573736079810999615542354866920007861214183738025983
length = 455
s = [135516280150137458535561766358086896198348823398876741567317041366935426854394060237235814065881756890818477438426875999503748746848408802883160976139168309216479723387043154316328752466115337006276833313025698482591954333004698732007362032602920842020200559463427548622804767419825141012760232500564198606888, 87138950331850035073233755923193357352015776817591237970872234630746818824503152055070348052111940612563932340910671611099400897135890145261451245577578879099083666861166614841834235097485990689182812564858373409987914436273165881047892580175317423057893816031028632720419872660582122916390309733324086153485, 138644295462947977586933469377687701489914340911921767410183452121042506019270712424245627451242649429408423057598802920666169608453899414528460692023716837136269325732757807484480055069814533664161537001762727348850128480964361110794017997076616622537153343830644577017008185863066319652708947485342513469942, 130919765117872700420555258668777170220585743300145967201676029268553369762501611700891574139388115937578229121079450407536963982339229719500478504489500235690293048515731859346431065030206394207045994366861194654126521065191859763903957682731311119322278004810859526215299984270862147897660764896871931296525, 114700370393183453087762195804219894122789831440066263230660331964018561704119945094712846882622289910478787117536755419287483635582978440493028286129198190921201156025431173751752743507530849046089710840106416071119787801330709608148349917138686962228418379795866832374558526179470426187199100866047189895398, 5526726757049511570122924251009639296817346269475117861098612689025237993752241296662636520025051472762072465223105287132204748691454643208692589407448303681720594661639751550346640974853714675951318971703834962983574657923366839131735681149307918005820142824780727533061358686675519367812942183782965460156, 144912005915009185433389709621768898379612902758176190094171990137016617813547436225820194585543950753591409962313416349983080186189291716456666174265994068233652987757656436662736504159419091874803636330149391525094620604417895137599924048423029008070688563937967247938795175561463188529887593887274447829757, 136250954616195732816473240575012270303125387854617764474032021538389021573726037002975200362404464882071072085887627232185387656472286476406393582907753248439212389626213347657516288312775908225085848334636924022113242155272938168661245231559256589332709251562390352253724058379737367174585436687621017694623, 62581851774850409035755528242738381905999051352008432547471965980273593728343556710086776830920012955472867109461528976241913935857428013748626805913556479910568244555311572298067590116614399220857206962127377751825672045446525674748896825242976163703599291103837976885179955618472741727241520609778322846005, 145854407984474847551927547284413490204495969306617565827750995876170774717809213321826036612782367152524129825636642176629348378245478404356883485091652713207020554564450132585121134356935492165152072283066165961023761302228624528890490009909363984222514631061033009247208437816124596049012309910840440309561, 124551623006909497965848991707513696948607938882176233365140848984406516643540438381538258922460588883294565931391660391812373244670311091543926813390568684148523894758100116918211999135492588543339785067482674405654655248001114133508625872962520401753384795662160688811171758878041475228921004115541651588149, 15938340419155549703292732921378484283671988749432038679365417994992859057494159116052524559743521485794692543381549875094855921795753932087886980295291140542937847588182771711846510176440458231173636452634043298156122152860644504752015830250690063832495966826188439527832958662817314634043438801092078111173, 86793422805279107846504839960808639992922541788273836408000957039906527697664805903722395255793430323591730573513732464380853123117859130756589515125491536316134863620706530836481623063642225089209431819777355554001327119466306759145993282751212553582691384017307673738794439532271560215747589628721710135897, 108675608374666743358023889479027512878400550037574532652565479774965642002565282273742545254311704772402696446846722391711332035309818100961301897022556307435354059324998874351394451945385491984524729822436607930537193897390621277431306545936473390631504396022406944910561421866589605078829721977335264154976, 87317748227288225233288224866786892964848811364878121564104341670954340348393418506174791619641614941888448848731903276361744955803183864888079233767189621441829023235771802783069311610169253651371628757455646066049167648114996530344278325612462268009587440597096690136975144034630898406289420602499264991623, 56652314874573546743584841968373113846850609963672297223607913939552862285375621862172324584570593402935091802803893885963277174956979046479939956703429737288793705461324779449285529662821030340203158503181009684937887687542388010343147675680002397630598445715400876202643169104742361423214638787268742234287, 98735788313453186782519834728824046613708479524564270665693218086798600541964070362862728960696910092702768075145925801913657156092005722008779014906938783990621453314812381950847944890837178907520481282447677162465215252648603374266972153988621533116563623242402366677831684416116807732808111964626488086987, 127540651954215161413641876933455408716614015796900097859173650400979733321781230732298931541274922911072112231027539634566966261240603321076224739659191443221985808678247919491141075440774231707687287562522535460013252508304387645505398442899700006526196099765002065480554613895222880144277349674640005507562, 133301958266564440496259158450519409455902192149222024966338884662576908051145274628854034018802181764563054480089111531034013218222971811942750317186820576575720998626362983321816936975595432624528396429872313110972358282919447478636004224335379606216720361742943716434992065840043748957089654449955193986860, 88160039502967812710045720428993741346375421128152598672398002732708719698481663322248764249302216242451840620334870977104442381110519298390156672581547539043729567682679341598750864890008905914145991583715826910836568061276943119691386206504777140515604809396852491015959654881350560399518061528959314304087]
c = 123907837039511977819816858353976764990739800475355111239750335121820426041872830656170595604631534502233882297517774737660499087852687022473212169680375890135271089504199640532421067201796868951827680690124297723304485612987566782809086630400500307531954278635605686302923551049889311808990254356288059153559

L = Matrix(ZZ, Count, Count)
L[0,0] = 2^length
for i in range(1, Count):
    L[0,i] = s[i]
    L[i,i] = -s[0]
res = L.LLL()[0]

q = s[0] // (res[0] // 2^length)
p = n // q
assert n == p*q

print(long_to_bytes(int(pow(c, inverse(e,(p-1)*(q-1)), n))))


#flag{Th3_Simultaneous_Diophantine_Approximation_Approach}

RSA

题目：

from Crypto.Util.number import *
from secrets import flag
m = bytes_to_long(flag)
p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 0x10001

M = matrix(Zmod(n), [
    [m, -m-p-q, -m-2*p, 2*q-m],
    [m+p+q,  m, 2*q-m,  m+2*p],
    [m+2*p,  m-2*q,  m, -m-p-q],
    [m-2*q, -m-2*p,  m+p+q,  m]
])

enc = M**e

print(f"n = {n}")
print(f"e = {e}")
print(list(enc))
n=13228298199631335610499409465400552275305629934024756614227830931136508640681372951453757994834844498763877490566164031828108583453919741685657210448857955666192855872103622943922893572765718705893238315297600050789804418329650168680719372191579207505092037294294875908952803670819999025123209403251314588474192758376162806705064430837428828805477906627599506069017651159117664246131790529354533675662936081996490294431369820750274303028529977278828959613343997326534446148884333619071935180484450320323844737055406889458275298296950269660857078186043669204168045730995355857013530919638304423700701901063780318208789
e=65537
enc=[(1491873293560323909465836471682585391496137454962536255211620436893391549603126009345148985699013899435764986980919290827837440218992944453711597495517127038406936254470963878149611067609857046502282994346483454884781103538081677117421537728730737422899739818406539050745938770868537148564365984825217449546939297237128543198112642950063626687602582556615437626388875069902892432216468378684299365817407995725759407957747215159745600867120912008194130121350313833434901083388223410629737737418961006112893999319596217781130922876695397872007871395908185274519733474161410964601075476672137735633842608230612826681061, 4956025543963860548224153175168493318238985854531591968596322951867101383038318092494673400475554880419342014784571362229741642826660412082585292197764604908450405263330703286845800303018092222139976907126517882830745820723998293430203137128739850924103620078289772876248014239067659155995114953314111131752812515097213052728067061893768763077056914111566820414025280534046400995356712414837449121046062079911435309295464490263283769221830037029108374974495201782045992874653920211537537724643230986981824349266978767367402293999209162694369772760075107747609491264902786041130826876918123202134703658442941891830242, 7710011511933273600956066580006667228795766247206337007278271463871915295714373557766306241838812677910529618690854981247073325175370147283360553440166198511565970962496527743224575526922830794861623489204146092991883999208502150565496732100104360091815826333424313805145648110936043125983239009895903602879010609096750963186952687545255588633288528372363096307287365891027749166227382683937570696463897150461450791183251190323380329123556440876127657763835466077899344290052877228945633508945118354870143193111572860186690380517929737934424809644493802524411423150714171313957036859668776471063633076408076909640002, 11534398990341303260469847611439061098979668999994719829731530111550470410818410249398161750557290507614569764189238005873703309686837109506327355518339608092717603460229057410906842405901627607535605010996612762231101162949308540690378638599362997229992351236008016988744038581908756449465377928987817065146363195497304246692426541055618255515479438494976345916998240594200316617809496338857712977577830501882906692816143225556486899297950715922558009978599642835535619697869607264637171021550028689009097951803276399427016025503188133689654404551377724037837852806988185689913776323215325531565269517783734339408476), (8272272655667475062275256290232058957066644079493164645631507979269407257643054858959084594359289618344535475781592669598366940627259329603071918251093350757742450608772919657077093269747626483753261408171082167959058597605651875250516235062839356580988417216005103032704789431752339869128094449937203456721380243278949753976997368943660065728420992516032685654992370625071263250775078114517084554616874002085054985135905330486990533806699940249720584638848795544488453274230413407534397455841219333342020387788428122090873004297741106966487305425968561456558554466092569815882704042720181221565998242620838426378547, 1491873293560323909465836471682585391496137454962536255211620436893391549603126009345148985699013899435764986980919290827837440218992944453711597495517127038406936254470963878149611067609857046502282994346483454884781103538081677117421537728730737422899739818406539050745938770868537148564365984825217449546939297237128543198112642950063626687602582556615437626388875069902892432216468378684299365817407995725759407957747215159745600867120912008194130121350313833434901083388223410629737737418961006112893999319596217781130922876695397872007871395908185274519733474161410964601075476672137735633842608230612826681061, 11534398990341303260469847611439061098979668999994719829731530111550470410818410249398161750557290507614569764189238005873703309686837109506327355518339608092717603460229057410906842405901627607535605010996612762231101162949308540690378638599362997229992351236008016988744038581908756449465377928987817065146363195497304246692426541055618255515479438494976345916998240594200316617809496338857712977577830501882906692816143225556486899297950715922558009978599642835535619697869607264637171021550028689009097951803276399427016025503188133689654404551377724037837852806988185689913776323215325531565269517783734339408476, 5518286687698062009543342885393885046509863686818419606949559467264593344966999393687451752996031820853347871875309050581035258278549594402296657008691757154626884909607095200698318045842887911031614826093453957797920419121148018115222640091474847413276210960870562103807155559883955899139970393355410985595182149279411843518111743292173240172189378255236409761730285268089915079904407845416962979199038931535039503248118630426893973904973536402701301849508531248635101858831456390126301671539331965453701543943834029271584917779020531726432268541549866679756622580281184543056494059969527952637068824655703408568787), (5518286687698062009543342885393885046509863686818419606949559467264593344966999393687451752996031820853347871875309050581035258278549594402296657008691757154626884909607095200698318045842887911031614826093453957797920419121148018115222640091474847413276210960870562103807155559883955899139970393355410985595182149279411843518111743292173240172189378255236409761730285268089915079904407845416962979199038931535039503248118630426893973904973536402701301849508531248635101858831456390126301671539331965453701543943834029271584917779020531726432268541549866679756622580281184543056494059969527952637068824655703408568787, 1693899209290032350029561853961491176325960934030036784496300819586038229862962702055596244277553991149307726376926025954405273767082632179329854930518347573475252411874565533016051166864091098357633304300987288558703255380341627990340733592216210275099686058286858920208765088911242575657831474263497523327829562878858560012637889781810573289998468132623160152019410564917347628322294190496820698085105580113583601615226595193787403730579261356270949634744354490998826451014726354434764158934421631314746785252130490031259272793762135971202673634665945166330192924007170167099754596422978892135432383280045978800313, 1491873293560323909465836471682585391496137454962536255211620436893391549603126009345148985699013899435764986980919290827837440218992944453711597495517127038406936254470963878149611067609857046502282994346483454884781103538081677117421537728730737422899739818406539050745938770868537148564365984825217449546939297237128543198112642950063626687602582556615437626388875069902892432216468378684299365817407995725759407957747215159745600867120912008194130121350313833434901083388223410629737737418961006112893999319596217781130922876695397872007871395908185274519733474161410964601075476672137735633842608230612826681061, 4956025543963860548224153175168493318238985854531591968596322951867101383038318092494673400475554880419342014784571362229741642826660412082585292197764604908450405263330703286845800303018092222139976907126517882830745820723998293430203137128739850924103620078289772876248014239067659155995114953314111131752812515097213052728067061893768763077056914111566820414025280534046400995356712414837449121046062079911435309295464490263283769221830037029108374974495201782045992874653920211537537724643230986981824349266978767367402293999209162694369772760075107747609491264902786041130826876918123202134703658442941891830242), (1693899209290032350029561853961491176325960934030036784496300819586038229862962702055596244277553991149307726376926025954405273767082632179329854930518347573475252411874565533016051166864091098357633304300987288558703255380341627990340733592216210275099686058286858920208765088911242575657831474263497523327829562878858560012637889781810573289998468132623160152019410564917347628322294190496820698085105580113583601615226595193787403730579261356270949634744354490998826451014726354434764158934421631314746785252130490031259272793762135971202673634665945166330192924007170167099754596422978892135432383280045978800313, 7710011511933273600956066580006667228795766247206337007278271463871915295714373557766306241838812677910529618690854981247073325175370147283360553440166198511565970962496527743224575526922830794861623489204146092991883999208502150565496732100104360091815826333424313805145648110936043125983239009895903602879010609096750963186952687545255588633288528372363096307287365891027749166227382683937570696463897150461450791183251190323380329123556440876127657763835466077899344290052877228945633508945118354870143193111572860186690380517929737934424809644493802524411423150714171313957036859668776471063633076408076909640002, 8272272655667475062275256290232058957066644079493164645631507979269407257643054858959084594359289618344535475781592669598366940627259329603071918251093350757742450608772919657077093269747626483753261408171082167959058597605651875250516235062839356580988417216005103032704789431752339869128094449937203456721380243278949753976997368943660065728420992516032685654992370625071263250775078114517084554616874002085054985135905330486990533806699940249720584638848795544488453274230413407534397455841219333342020387788428122090873004297741106966487305425968561456558554466092569815882704042720181221565998242620838426378547, 1491873293560323909465836471682585391496137454962536255211620436893391549603126009345148985699013899435764986980919290827837440218992944453711597495517127038406936254470963878149611067609857046502282994346483454884781103538081677117421537728730737422899739818406539050745938770868537148564365984825217449546939297237128543198112642950063626687602582556615437626388875069902892432216468378684299365817407995725759407957747215159745600867120912008194130121350313833434901083388223410629737737418961006112893999319596217781130922876695397872007871395908185274519733474161410964601075476672137735633842608230612826681061)]

题目给出了一个奇怪的矩阵M：

$M = \left(\begin{matrix} m & -m-p-q & -m-2*p & 2*q-m\\ m+p+q & m & 2*q-m & m+2*p\\ m+2*p & m-2*q & m & -m-p-q\\ m-2*q & -m-2*p & m+p+q & m\\ \end{matrix}\right)$

除了RSA的公钥n、e之外再给出$C=M^e$，要求m。

M显然有点特殊，所以先拆成一个反对称阵和单位阵的和形式：

$A = \left(\begin{matrix} 0 & -m-p-q & -m-2*p & 2*q-m\\ m+p+q & 0 & 2*q-m & m+2*p\\ m+2*p & m-2*q & 0 & -m-p-q\\ m-2*q & -m-2*p & m+p+q & 0\\ \end{matrix}\right)$ $M = A + mE$

所以有：

$C = M^e = (A + mE)^e$

这样出来了一个二项式定理的形式，那么把他展开就得到：

$C = A^e + emA^{e-1} + (\frac{e}{2})m^2A^{e-2} + ... + em^{e-1}A + m^eE$

自己测试一下会发现A的偶次幂是个对角矩阵，因此最终C的非对角线元素都是上述二项式展开中A的奇数次幂贡献的。用小一点的e去factor一下非对角线元素的因子会发现这些和式均有共同因子：

PR.<m,p,q> = PolynomialRing(ZZ)
M = matrix([
    [m, -m-p-q, -m-2*p, 2*q-m],
    [m+p+q,  m, 2*q-m,  m+2*p],
    [m+2*p,  m-2*q,  m, -m-p-q],
    [m-2*q, -m-2*p,  m+p+q,  m]
])

A = matrix([
    [0, -m-p-q, -m-2*p, 2*q-m],
    [m+p+q,  0, 2*q-m,  m+2*p],
    [m+2*p,  m-2*q,  0, -m-p-q],
    [m-2*q, -m-2*p,  m+p+q,  0]
])

E = Matrix(ZZ, identity_matrix(4))

print(factor((A^1)[1,0]))
print(factor((A^3)[1,0]))
print(factor((A^5)[1,0]))
print(factor((A^7)[1,0]))

输出：

m + p + q
(-1) * (m + p + q) * (3*m^2 + 6*m*p + 5*p^2 - 2*m*q + 2*p*q + 5*q^2)
(m + p + q) * (3*m^2 + 6*m*p + 5*p^2 - 2*m*q + 2*p*q + 5*q^2)^2
(-1) * (m + p + q) * (3*m^2 + 6*m*p + 5*p^2 - 2*m*q + 2*p*q + 5*q^2)^3

所以可以提取出几组C中的代数关系：

1
2
3

(m + 2*p)*enc[1,0] == (m + p + q)*enc[2,0]
(m - 2*q)*enc[1,0] == (m + p + q)*enc[3,0]
p*q == n

然后groebner就可以解掉。

exp：

from Crypto.Util.number import *

n = 13228298199631335610499409465400552275305629934024756614227830931136508640681372951453757994834844498763877490566164031828108583453919741685657210448857955666192855872103622943922893572765718705893238315297600050789804418329650168680719372191579207505092037294294875908952803670819999025123209403251314588474192758376162806705064430837428828805477906627599506069017651159117664246131790529354533675662936081996490294431369820750274303028529977278828959613343997326534446148884333619071935180484450320323844737055406889458275298296950269660857078186043669204168045730995355857013530919638304423700701901063780318208789
e = 65537
enc = [(1491873293560323909465836471682585391496137454962536255211620436893391549603126009345148985699013899435764986980919290827837440218992944453711597495517127038406936254470963878149611067609857046502282994346483454884781103538081677117421537728730737422899739818406539050745938770868537148564365984825217449546939297237128543198112642950063626687602582556615437626388875069902892432216468378684299365817407995725759407957747215159745600867120912008194130121350313833434901083388223410629737737418961006112893999319596217781130922876695397872007871395908185274519733474161410964601075476672137735633842608230612826681061, 4956025543963860548224153175168493318238985854531591968596322951867101383038318092494673400475554880419342014784571362229741642826660412082585292197764604908450405263330703286845800303018092222139976907126517882830745820723998293430203137128739850924103620078289772876248014239067659155995114953314111131752812515097213052728067061893768763077056914111566820414025280534046400995356712414837449121046062079911435309295464490263283769221830037029108374974495201782045992874653920211537537724643230986981824349266978767367402293999209162694369772760075107747609491264902786041130826876918123202134703658442941891830242, 7710011511933273600956066580006667228795766247206337007278271463871915295714373557766306241838812677910529618690854981247073325175370147283360553440166198511565970962496527743224575526922830794861623489204146092991883999208502150565496732100104360091815826333424313805145648110936043125983239009895903602879010609096750963186952687545255588633288528372363096307287365891027749166227382683937570696463897150461450791183251190323380329123556440876127657763835466077899344290052877228945633508945118354870143193111572860186690380517929737934424809644493802524411423150714171313957036859668776471063633076408076909640002, 11534398990341303260469847611439061098979668999994719829731530111550470410818410249398161750557290507614569764189238005873703309686837109506327355518339608092717603460229057410906842405901627607535605010996612762231101162949308540690378638599362997229992351236008016988744038581908756449465377928987817065146363195497304246692426541055618255515479438494976345916998240594200316617809496338857712977577830501882906692816143225556486899297950715922558009978599642835535619697869607264637171021550028689009097951803276399427016025503188133689654404551377724037837852806988185689913776323215325531565269517783734339408476), (8272272655667475062275256290232058957066644079493164645631507979269407257643054858959084594359289618344535475781592669598366940627259329603071918251093350757742450608772919657077093269747626483753261408171082167959058597605651875250516235062839356580988417216005103032704789431752339869128094449937203456721380243278949753976997368943660065728420992516032685654992370625071263250775078114517084554616874002085054985135905330486990533806699940249720584638848795544488453274230413407534397455841219333342020387788428122090873004297741106966487305425968561456558554466092569815882704042720181221565998242620838426378547, 1491873293560323909465836471682585391496137454962536255211620436893391549603126009345148985699013899435764986980919290827837440218992944453711597495517127038406936254470963878149611067609857046502282994346483454884781103538081677117421537728730737422899739818406539050745938770868537148564365984825217449546939297237128543198112642950063626687602582556615437626388875069902892432216468378684299365817407995725759407957747215159745600867120912008194130121350313833434901083388223410629737737418961006112893999319596217781130922876695397872007871395908185274519733474161410964601075476672137735633842608230612826681061, 11534398990341303260469847611439061098979668999994719829731530111550470410818410249398161750557290507614569764189238005873703309686837109506327355518339608092717603460229057410906842405901627607535605010996612762231101162949308540690378638599362997229992351236008016988744038581908756449465377928987817065146363195497304246692426541055618255515479438494976345916998240594200316617809496338857712977577830501882906692816143225556486899297950715922558009978599642835535619697869607264637171021550028689009097951803276399427016025503188133689654404551377724037837852806988185689913776323215325531565269517783734339408476, 5518286687698062009543342885393885046509863686818419606949559467264593344966999393687451752996031820853347871875309050581035258278549594402296657008691757154626884909607095200698318045842887911031614826093453957797920419121148018115222640091474847413276210960870562103807155559883955899139970393355410985595182149279411843518111743292173240172189378255236409761730285268089915079904407845416962979199038931535039503248118630426893973904973536402701301849508531248635101858831456390126301671539331965453701543943834029271584917779020531726432268541549866679756622580281184543056494059969527952637068824655703408568787), (5518286687698062009543342885393885046509863686818419606949559467264593344966999393687451752996031820853347871875309050581035258278549594402296657008691757154626884909607095200698318045842887911031614826093453957797920419121148018115222640091474847413276210960870562103807155559883955899139970393355410985595182149279411843518111743292173240172189378255236409761730285268089915079904407845416962979199038931535039503248118630426893973904973536402701301849508531248635101858831456390126301671539331965453701543943834029271584917779020531726432268541549866679756622580281184543056494059969527952637068824655703408568787, 1693899209290032350029561853961491176325960934030036784496300819586038229862962702055596244277553991149307726376926025954405273767082632179329854930518347573475252411874565533016051166864091098357633304300987288558703255380341627990340733592216210275099686058286858920208765088911242575657831474263497523327829562878858560012637889781810573289998468132623160152019410564917347628322294190496820698085105580113583601615226595193787403730579261356270949634744354490998826451014726354434764158934421631314746785252130490031259272793762135971202673634665945166330192924007170167099754596422978892135432383280045978800313, 1491873293560323909465836471682585391496137454962536255211620436893391549603126009345148985699013899435764986980919290827837440218992944453711597495517127038406936254470963878149611067609857046502282994346483454884781103538081677117421537728730737422899739818406539050745938770868537148564365984825217449546939297237128543198112642950063626687602582556615437626388875069902892432216468378684299365817407995725759407957747215159745600867120912008194130121350313833434901083388223410629737737418961006112893999319596217781130922876695397872007871395908185274519733474161410964601075476672137735633842608230612826681061, 4956025543963860548224153175168493318238985854531591968596322951867101383038318092494673400475554880419342014784571362229741642826660412082585292197764604908450405263330703286845800303018092222139976907126517882830745820723998293430203137128739850924103620078289772876248014239067659155995114953314111131752812515097213052728067061893768763077056914111566820414025280534046400995356712414837449121046062079911435309295464490263283769221830037029108374974495201782045992874653920211537537724643230986981824349266978767367402293999209162694369772760075107747609491264902786041130826876918123202134703658442941891830242), (1693899209290032350029561853961491176325960934030036784496300819586038229862962702055596244277553991149307726376926025954405273767082632179329854930518347573475252411874565533016051166864091098357633304300987288558703255380341627990340733592216210275099686058286858920208765088911242575657831474263497523327829562878858560012637889781810573289998468132623160152019410564917347628322294190496820698085105580113583601615226595193787403730579261356270949634744354490998826451014726354434764158934421631314746785252130490031259272793762135971202673634665945166330192924007170167099754596422978892135432383280045978800313, 7710011511933273600956066580006667228795766247206337007278271463871915295714373557766306241838812677910529618690854981247073325175370147283360553440166198511565970962496527743224575526922830794861623489204146092991883999208502150565496732100104360091815826333424313805145648110936043125983239009895903602879010609096750963186952687545255588633288528372363096307287365891027749166227382683937570696463897150461450791183251190323380329123556440876127657763835466077899344290052877228945633508945118354870143193111572860186690380517929737934424809644493802524411423150714171313957036859668776471063633076408076909640002, 8272272655667475062275256290232058957066644079493164645631507979269407257643054858959084594359289618344535475781592669598366940627259329603071918251093350757742450608772919657077093269747626483753261408171082167959058597605651875250516235062839356580988417216005103032704789431752339869128094449937203456721380243278949753976997368943660065728420992516032685654992370625071263250775078114517084554616874002085054985135905330486990533806699940249720584638848795544488453274230413407534397455841219333342020387788428122090873004297741106966487305425968561456558554466092569815882704042720181221565998242620838426378547, 1491873293560323909465836471682585391496137454962536255211620436893391549603126009345148985699013899435764986980919290827837440218992944453711597495517127038406936254470963878149611067609857046502282994346483454884781103538081677117421537728730737422899739818406539050745938770868537148564365984825217449546939297237128543198112642950063626687602582556615437626388875069902892432216468378684299365817407995725759407957747215159745600867120912008194130121350313833434901083388223410629737737418961006112893999319596217781130922876695397872007871395908185274519733474161410964601075476672137735633842608230612826681061)]
enc = Matrix(Zmod(n), enc)

########################################### 
#(m + 2*p)*enc[1,0] == (m + p + q)*enc[2,0]
#(m - 2*q)*enc[1,0] == (m + p + q)*enc[3,0]
#p*q == n

PR.<m,p,q> = PolynomialRing(Zmod(n))
f1 = (m + 2 * p) - (inverse(enc[1,0],n)*enc[2,0])*(m + p + q)
f2 = (m - 2 * q) - (inverse(enc[1,0],n)*enc[3,0])*(m + p + q)
f3 = p*q
res = Ideal([f1,f2,f3]).groebner_basis()
for i in res:
    print(i)

q = 98199204383444167136509999317652307746300154257439691314026803510437035509888229764173492052858804263577571331383214859652229706329210472593337809065208882042178413249493877596701444929209070708258353144837330382092255133776768117120874000890494449018234172972678168219613884207547781528635959091301251971281
p = n // q
assert p*q == n

PR.<m> = PolynomialRing(Zmod(n))
f = (m + 2 * p) - (inverse(enc[1,0],n)*enc[2,0])*(m + p + q)
#print(f)
flag = inverse(3297056809289327500256202079127136134187438944961708132751779704042134248345975436322191479293257096389543469387818190390952261259850867719244868774056284786555129809594382750795637970645528822198427409878547718771238431341613753773735778866319889665322786887273473714741059398430312523411707495791556075878244637630480194633873896328931631465317325085583101546945701547571540285337915330695525854299979138422312974757786532911019780366620715999126086808046470039825598115253747158220517041862628277627457873544852999345612018379688444091864667014856637790925604130983328623143861756949881991846056060324187971651968,n) * (-1498891588977545370451304005269054204989297955532246655702497171972634294190353786886109979315712227670838063747138944971165078237866699516737057265958406033545290094866918511445027202221306581865115556251808822409761737528633460237914954126481851519653767357154958076960906373574059921391655491951867500826108554012342761055413189807372591262833424798009944360120455674246600349563624996782442874590028504156102295527090123626799675614654662807183634567377812300847810842883813710868799454486184658344859843573551816770639242317817513006458632518373823719039586807296528828652532914106040726579904539566401034957917)

print(long_to_bytes(int(flag) % n))


#WMCTF{QU4t3rni0n_4nd_Matr1x_4r3_4un}

C O N N E C T 1 0 N

题目描述：

1	Hand 1n Hand, Heart t0 Heart

题目：

from Crypto.Util.number import *
from os import urandom
import random
from secret import flag

def padding(flag,length):
    head_length = random.randint(1,length-len(flag))
    tail_length = length-len(flag)-head_length
    while 1:
        re = urandom(head_length)+flag+urandom(tail_length)
        if (bin(bytes_to_long(re)).count('1')) % 2:
            return re

def shuffle(left,right):
    xor_string = [0]*left+[1]*right
    random.shuffle(xor_string)
    xor_string = int(''.join(str(i) for i in xor_string),2)
    return xor_string

l,r = 63,65
flag = padding(flag,(len(flag)//4+1)*4)
S = [bytes_to_long(padding(flag[len(flag)//4*i:len(flag)//4*(i+1)],(l+r)//8)) for i in range(4)]
data = [[[shuffle(r,l)^^S[_] if j == '1' else shuffle(l,r)^^S[_] for j in (bin(shuffle(r,l)^^S[_])[2:].rjust(l+r,'0') if i == '1' else bin(shuffle(l,r)^^S[_])[2:].rjust(l+r,'0'))] for i in bin(S[_])[2:].rjust(l+r,'0')] for _ in range(4)]

print(data)

output很长不放在这里，自己本地生成些数据做也是一样的。

这次来自@yolbby ，当时他出完之后我验了这道题，所以就没有在赛中打。

yolbby出题很有意思，先只管出，然后我们一起再看能不能做XD

这题是他之前给他们学校招新赛的躲猫猫中一个题目的升级，不过真的升级太多了，所以打法完全不一样，因此也没有必要去找那个题目做参考。

总而言之题目加密流程如下：

将flag前后填上随机字节，使得其填充至指定长度，并保证填充后的flag的0、1比特数量不同
把flag分成长度相等的四部分，并转为整数，记在列表S里
对S中的每一部分分别进行后续加密

由于S的四部分都是分开的，所以假设就加密第一部分好了。

因为这么做可以少一层括号，括号多了真的头大TT

先看一下shuffle这个函数，对于输入(l，r)，它的功能是输出一个随机比特串，但这个比特串0的数量为l，1的数量为r。

又因为题目生成的随机串只有(63,65)和(65,63)两种，不妨就把他们分别记为串a和串b，并记S[0]对应的比特串是m，那么加密流程是：

对m按位加密，记当前位为s（以下以当前bit为1举例）：
如果s = 1，则生成随机串b1，并记：
- 对于c的每一位，记当前位为t，
- 如果t = 1，则生成随机串b2，并计算d，放到data中：
  $d = b_2 \oplus m$
- 如果t = 0，则生成随机串a2，并计算e，放到data中：
  $e = a_2 \oplus m$

由于内外套了两层与m的异或，很难直接看出什么性质，所以我们不妨先假设一个简化的情形，也就是外层不与m异或：

data = [[shuffle(r,l)^^secret if j == '1' else shuffle(l,r)^^secret for j in (bin(shuffle(r,l))[2:].rjust(128,'0') if i == '1' else bin(shuffle(l,r))[2:].rjust(128,'0'))] for i in bin(secret)[2:].rjust(128,'0')]

此时我们知道，如果m当前位s=1，那么data对应的这一行会有65个e串，63个d串；否则会有63个e串，65个d串。

m和data中的数据都是一个128bit的比特串，我们考虑对他们做一个映射：

$\phi: (\{0,1\},\oplus) \rightarrow (\{1,-1\},\times)$

这个映射显然是个同态，因为：

$\phi(x_1 \oplus x_2) = \phi(x_1) \times \phi(x_2)$

我们用data中的第一行展开分析，记第一行中每个数据分别为ci，那么此时m与ci的异或就可以同态到乘法：

$m \oplus c_i \rightarrow (m'_{1}c'_{i1},m'_{2}c'_{i2},...,m'_{128}c'_{i,128})$

而我们知道m与ci的异或值要么是a串要么是b串，而由于a、b两种串做映射后变成1、-1的数量相差2，所以这其实告诉了我们一个映射后向量的内积关系：

$\mathbf{m'} \cdot \mathbf{c_i'} = \pm 2$

而这具体是2还是-2我们暂时不得而知，因为我们不清楚每个ci对应的是d串还是e串，但是有一个事情是确定的，那就是第一行d、e两种串的数量分别是63或者65，具体a是63还是b是63取决于m的第一bit。

既然总量上有差异，那么考虑把第一行所有内积进行加和，就得到：

$\mathbf{m'} \cdot \sum_{i = 1}^{128} \mathbf{c_i'} = \pm 4$

之所以是正负4，这是因为有63对两两抵消掉了，只剩下单出来的两个a串或b串，所以为正负4。

而现在要解决的问题是：到底每一行是正4还是-4？我们知道m当前bit如果是0，这一行d串更多，那么加和中会单出两个b串，所以会得到4；同理如果m当前bit是1就会得到-4。因此我们可以把所有加和写成一个矩阵方程：

$\mathbf{m'} \cdot \sum_{i = 1}^{128}\sum_{j = 1}^{128} \mathbf{c_{ij}'} = 4\mathbf{m'}$

把cij组成的矩阵记作M，就有：

$\mathbf{m'}M = 4\mathbf{m'}$

也就是：

$\mathbf{m'}(M - 4E) = (0,0,...,0)$

所以如果是这种情况就简单了，我们只需要求矩阵方程就可以得到m’，再映射回m。

在这个思路基础上，题目在外层多套了一层与m的异或，这使得下面的式子不一定成立：

$\mathbf{m'} \cdot \sum_{i = 1}^{128} \mathbf{c_i'} = \pm 4$

此时成立的应该是：（因为每更换一bit就会少一对a、b串，而多出两个单的a串或b串）

$\mathbf{m'} \cdot \sum_{i = 1}^{128} \mathbf{c_i'} = \pm 4k$

那么就有：

$\mathbf{m'} M = (0,0,...,0) \quad(mod\;4)$

而实际上进一步测试可以发现m一定满足且仅满足如下两种情况之一，具体是哪种取决于m汉明重量的奇偶性，事实上由于padding的特殊性一定满足模8为0：

$\mathbf{m'} M = (4,4,...,4) \quad(mod\;8)$ $\mathbf{m'} M = (0,0,...,0) \quad(mod\;8)$

不过不管哪种情况，由于m’是1、-1组成的短向量所以都可以BKZ。

exp：

from Crypto.Util.number import *

with open(r"output.txt", "r") as f:
    data = eval(f.readline())

for datai in data:
    M = matrix(128,128)
    v0 = zero_matrix(128)[0]

    M = matrix(128,128)
    for i in range(128):
        for j in range(128):
            temp = bin(datai[i][j])[2:].zfill(128)
            m = [-1 if tt == '1' else 1 for tt in temp]
            for k in range(128):
                M[k,i] += m[k]

    L = block_matrix(ZZ,[
        [identity_matrix(128),M],
        [0,8*identity_matrix(128)]
    ])
    L[:,-128:] *= 2^10

    res = L.BKZ(block_size=28)
    for i in res:
        if(all (j == 1 or j == -1 for j in i[:128])):
            flag1 = ""
            flag2 = ""
            for t in i[:128]:
                if(t == -1):
                    flag1 += "0"
                    flag2 += "1"
                else:
                    flag1 += "1"
                    flag2 += "0"
            print(long_to_bytes(int(flag1,2)))
            print(long_to_bytes(int(flag2,2)))


#WMCTF{CW
#02nec71on_Pw
#TUnSt4b13_2v
#_under_3L}

#WMCTF{C02nec71on_UnSt4b13_under_3L}

*Turing

题目描述：

1	Do as Turing did.

题目：

重要一点的文件大概是以下几个：

from hashlib import sha256
import socketserver
import signal
import string
import random
import os
from string import ascii_uppercase
from random import shuffle, choice, randint
from pyenigma import *
from myenigma import myReflector, myrotors

flag = 


def check(s1, s2):
    if len(s1) != len(s2):
        return False
    count = 0
    for i in range(len(s1)):
        if s1[i] == s2[i]:
            count += 1
    if (count/len(s1)) > 0.85:
        return True
    return False


class Task(socketserver.BaseRequestHandler):
    def _recvall(self):
        BUFF_SIZE = 2048
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline:
                msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self, prompt=b'[-] '):
        self.send(prompt, newline=False)
        return self._recvall()

    def proof_of_work(self):
        signal.alarm(60)
        random.seed(os.urandom(8))
        proof = ''.join(
            [random.choice(string.ascii_letters+string.digits) for _ in range(20)])
        _hexdigest = sha256(proof.encode()).hexdigest()
        self.send(f"[+] sha256(XXXX+{proof[4:]}) == {_hexdigest}".encode())
        x = self.recv(prompt=b'[+] Plz tell me XXXX: ')
        if len(x) != 4 or sha256(x+proof[4:].encode()).hexdigest() != _hexdigest:
            return False
        return True

    def handle(self):
        if not self.proof_of_work():
            self.send(b'[!] Wrong!')
            return
        signal.alarm(150)
        key = ?
        letters = list(ascii_uppercase)
        others = "".join([choice(letters) for i in range(30)])
        pos = randint(0, len(others))
        text = others[:pos]+key+others[pos:]
        dayrotors = tuple(random.sample(myrotors, 3))
        for times in range(10):
            tmpkey = "".join([choice(letters) for i in range(3)])
            shuffle(letters)
            plugin = " ".join([letters[2*i]+letters[2*i+1] for i in range(10)])
            myEnigma = enigma.Enigma(myReflector, *dayrotors, tmpkey, plugin)
            ctx = myEnigma.encipher(text)
            self.send(ctx.encode())
        datekey = "".join([choice(letters) for i in range(3)])
        shuffle(letters)
        plugin = " ".join([letters[2*i]+letters[2*i+1] for i in range(10)])
        myEnigma = enigma.Enigma(myReflector, *dayrotors, datekey, plugin)
        ctx = myEnigma.encipher(text)
        self.send(ctx.encode())
        self.send(b"now give me the plaintext:")
        ans = self.recv().decode()

        if not check(ans, text):
            self.send(b'nonono')
            return

        self.send(b'here is your flag')
        self.send(flag)


class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass


class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
    pass


if __name__ == "__main__":
    HOST, PORT = '0.0.0.0', 8840
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    print(HOST, PORT)
    server.serve_forever()

msg.txt：

Some of the German ciphertexts have been decrypted. Maybe you can find something different.

SIXOCLOCKTHEWEATHERTODAYISCLEARRAININTHEEVENING
HEILHITLERMORNINGGREETINGSTHEWEATHERTODAYISRAINYSUNNYLATER
GOODMORNINGHOWAREYOUTHEWEATHERTODAYISCLOUDYWITHASLIGHTCHANCEOFSHOWERS
HIHOHEILHITLERTHEWEATHERTODAYISHOTANDHUMID
GREETINGSTHEWEATHERTODAYISWINDYANDCOLDTAKEGOODCARE
HELLOTHEWEATHERTODAYISSUNNYANDBRIGHTHAVEAGREATDAY
HEILHITLERMORNINGTHEWEATHERTODAYISFOGGYINTHEMORNINGCLEARINGUPLATER
HIHOWASYOURNIGHTTHEWEATHERTODAYISCOOLANDPLEASANT
GOODMORNINGHEILHITLERTHEWEATHERTODAYISRAINYWITHATHUNDERSTORMLATER
HELLOTHEWEATHERTODAYISHOTANDDRYREMEMBERTODRINKWATER
MORNINGGREETINGSTHEWEATHERTODAYISMISTYANDMOISTFEELINGREFRESHING

由于确实一点都不了解enigma，所以要先找点东西学习一下，结合题目描述知道应该是要考图灵对enigma的破译，所以找了以下一些资料看：

(99+ 封私信 / 80 条消息) 《模仿游戏》中艾伦·图灵是如何破译英格玛的？ - 知乎 (zhihu.com)

【中字】二战间谍战——英格玛密码机下（解密）@阿尔法小分队科教组_哔哩哔哩_bilibili

【计算机博物志】战争密码（下集）炸弹机_哔哩哔哩_bilibili

看完这几个会发现不管是加密方式还是破译方式，enigma都比想象的要简单很多，先简单总结一下。

组成

对于题目中的enigma，它有以下几个主要部件：

五个加密转子(rotor)：每个转子代表着一个字母间的单表代换，记为I、II、III、IV、V。
一个反射器，仍然代表一个单表代换
一个插线板(plugin)：在输入和输出时将插线板连接的字母进行交换

密钥

每次加密时有以下一些不同的配置，这些配置共同构成本次enigma加密的密钥：

五个rotors里面选取其中三个并作排列，如：IV、V、II

种数共有 $A(5,3) = 5 \cdot 4 \cdot 3 = 60$
每个被选中的rotor需要设置一个起始刻度，如：Q、V、M

种数共有 $26^3 = 17576$ 种
插线板需要选择十对字母两两组合，如：AB、CD、EF、GH、IJ、KL、MN、OP、QR、ST

种数共有 $\prod_{i=0}^{9}(\frac{26-2i}{2}) \approx 2^{69}$ 种

剩下没有配对的六个字母可以看作自己和自己交换(也就是不交换)，如：UU、VV、WW、XX、YY、ZZ

所以一次enigma加密的密钥可以看成一个三元组：

key =（（IV、V、II）、（Q、V、M）、（AB、CD、EF、GH、IJ、KL、MN、OP、QR、ST））

对于破译者来说，如果这三个元素都获得了，就可以解本次enigma的全部密文。

加密

简单来讲，enigma加密的输入输出都是一个英语字母串，并且是按字符来的。我们不妨假设明文是TANG，那么以T这单个字符被上述密钥加密为例，具体来说过程是：

输入T，经过plugin，变为S
B经过第一层转子IV，变为$\alpha$
$\alpha$经过第二层转子V，变为$\beta$
$\beta$经过第三层转子II，变为$\delta$
$\delta$经过反射器，变为$\gamma$
$\gamma$经过第三层转子II，变为$\theta$
$\theta$经过第二层转自V，变为$\epsilon$
$\epsilon$经过第一层转子IV，假设变为E
E经过plugin，变为F

这就是单次字符加密的全过程，而随着输入字符变多，三个rotor会按如下规律转动(不然为什么叫转子)：

每输入一个字符，第一层转子转动一格
第一层转子转动一圈，第二个转子就转动一格
第二层转子转动一圈，第三个转子就转动一格

所以在第一个字符T被加密之后，第一个转子会转一格，那么我们加密第二个字符A的时候第一个转子的单表代换就发生了改变，所以即使第二个输入字母还是T，他的结果也不会和第一个相同。

具体来说对于字符的一次加密流程图如下：（这个图少了plug的部分）

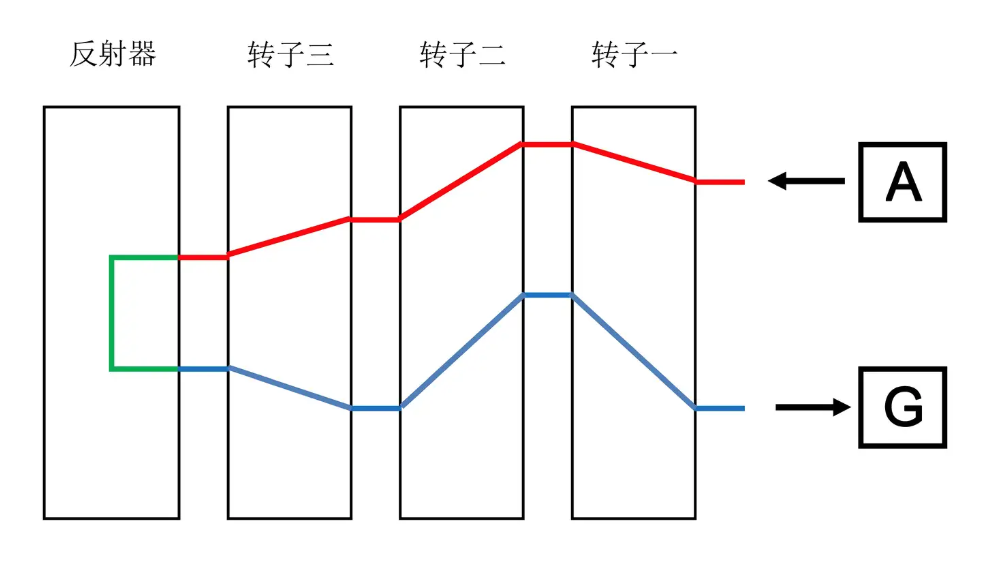
性质

enigma机主要有两个重要性质：

如果转子配置与plugin配置完全一样，那么如果加密 $\alpha$ 得到 $\beta$，在同样的配置下则一定有加密 $\beta$ 得到 $\alpha$，这个性质也叫自反性

从上面的单字符加密示意图也可以看出来，这有点光路图的感觉，而光路是可逆的XD，所以有完整密钥三元组的话，只需要用密钥配置enigma机，然后加密一遍密文就行了
任何字符在任何转子配置下一定不会加密得到其本身，也就是无论什么时候加密 $\alpha$ 都一定不会得到 $\alpha$

了解上面这些对这个题目就已经差不多了，接下来就回到题目。

题目

题意很简单：

连接上靶机后，靶机先生成30个随机英语字母，然后随机选定一个位置pos，在pos处插入一段key，得到待加密的明文text
用不同的enigma密钥对text进行加密，并发送密文，重复11次(10次tmpkey和1次datekey本质上来说没啥区别)
不同的enigma密钥指密钥的三个部分都完全不同：
- 随机选的三个rotors以及排列顺序
- 三个rotors对应的起始刻度
- plugin的设置
要求我们在150s内发送回一段文本ans，ans和text相同字母占比超过0.85就可以拿到flag

恢复text中的key

我们除了密文以外没有关于密钥的任何信息，好在题目还给了个task里完全没有出现过的msg，而很容易就联想到这个msg的内容应该和未知的静态key有关，而最合理的猜测就是key就在这段msg中。

与靶机简单交互一下会发现key的长度应该是17，所以现在的问题就是key究竟是msg中的哪17个字符。

此时我们就要利用上面讲的第二个性质：任何字符在任何转子配置下一定不会加密得到其本身，所以我们可以拿msg中的所有17个连续字符来与每次交互的11个密文做比对。具体步骤类似于滑动窗口，我们可以把11个密文以及我们假设的长为17的key一起排列起来，如下：

OSXJMOYNOBIUZBYHLTMLIMUDTBICTWVXSZEKHKAVPJKSLIP
KXORTUUSVUXTTPILXXPXYKOSHJJNVYHWYGPMAWXPPDYVRFB
EXFQKJIHGJNDPUQNLLCDWPQSFLBZRXPQKJYUDVDNARPLNJC
ZYYGFLWHSOQAFJAYKUNKQUEWNGIRQCTJSEDAGGOLPEUOCIV
FAZUNPEFDRKUOZXYAYRCRSEJTPFRHHODCQDCVMAWQBAKWXQ
AYNWCKPGAHMRATCQAFZNUZTTHCICBYEXLXTGPOYNIINBEMR
OAWFCWZMJWYAWNUNJNBDMLKGNNLTETMXJEGRDPXTZNHGEJK
TCHIIJVNOVHUWLUFUQMWJHPXZHBUOXLKWVBMWXXJNDYOJKM
QOMDJITPSUGFPCJTHJGZXISEVGQIWBKNQCFYROCZJBITTBK
IIOKAPDFKFZRPKDJMAXNQYONBYDRSFREUDWBQWHXLVQUJNS
FISNDRDZBHKJISFHVJXNRMRFAHCPILZANOUONMEGZGNFLXP

XXXXXXXXXXXXXXXXX

我们可以爆破msg里所有17个连续字符当作这段XXXXXXXXXXXXXXXXX，虽然位置pos我们并不知道，但是有一个事情是定的：这11个密文加密的都是同一个text，也就是key被加密的位置一样，所以如果当前爆破的key能够满足下面条件的话：

key在某一个pos，与上面11段密文在当前位置的那一段都没有相同的字符

这就说明它满足enigma的性质，就有可能是正确的key，反之则一定不是正确的key，可以用代码简单验证一下：

from pyenigma import rotor 
from string import ascii_uppercase
import random
from pyenigma import *
from itertools import *
from tqdm import *
from random import randint,choice,shuffle

########################################################################## data
myReflector=rotor.Reflector('WOEHCKYDMTFRIQBZNLVJXSAUGP',"myReflector")
myrotor1=rotor.Rotor('UHQAOFBEPIKZSXNCWLGJMVRYDT',"A",name="myrotor1")
myrotor2=rotor.Rotor('RIKHFBUJDNCGWSMZVXEQATOLYP',"A",name="myrotor2")
myrotor3=rotor.Rotor('ENQXUJSIVGOMRLHYCDKTPWAFZB',"A",name="myrotor3")
myrotor4=rotor.Rotor('JECGYWNDPQUSXZMKHRLTAVFOIB',"A",name="myrotor4")
myrotor5=rotor.Rotor('EYDBNSFAPJTMGURLOIWCHXQZKV',"A",name="myrotor5")
myrotors=[myrotor1,myrotor2,myrotor3,myrotor4,myrotor5]

msgs = ["SIXOCLOCKTHEWEATHERTODAYISCLEARRAININTHEEVENING",
"HEILHITLERMORNINGGREETINGSTHEWEATHERTODAYISRAINYSUNNYLATER",
"GOODMORNINGHOWAREYOUTHEWEATHERTODAYISCLOUDYWITHASLIGHTCHANCEOFSHOWERS",
"HIHOHEILHITLERTHEWEATHERTODAYISHOTANDHUMID",
"GREETINGSTHEWEATHERTODAYISWINDYANDCOLDTAKEGOODCARE",
"HELLOTHEWEATHERTODAYISSUNNYANDBRIGHTHAVEAGREATDAY",
"HEILHITLERMORNINGTHEWEATHERTODAYISFOGGYINTHEMORNINGCLEARINGUPLATER",
"HIHOWASYOURNIGHTTHEWEATHERTODAYISCOOLANDPLEASANT",
"GOODMORNINGHEILHITLERTHEWEATHERTODAYISRAINYWITHATHUNDERSTORMLATER",
"HELLOTHEWEATHERTODAYISHOTANDDRYREMEMBERTODRINKWATER",
"MORNINGGREETINGSTHEWEATHERTODAYISMISTYANDMOISTFEELINGREFRESHING"]
msg = "".join(msgs)


ciphers = []
keypos = randint(0,len(msg)-17)
key = msg[keypos:keypos+17]
letters = list(ascii_uppercase)
others = "".join([choice(letters) for i in range(30)])
pos = randint(0, len(others))
text = others[:pos]+key+others[pos:]
dayrotors = tuple(random.sample(myrotors, 3))
for times in range(10):
    tmpkey = "".join([choice(letters) for i in range(3)])
    shuffle(letters)
    plugin = " ".join([letters[2*i]+letters[2*i+1] for i in range(10)])
    myEnigma = enigma.Enigma(myReflector, *dayrotors, tmpkey, plugin)
    ctx = myEnigma.encipher(text)
    ciphers.append(ctx)
datekey = "".join([choice(letters) for i in range(3)])
shuffle(letters)
plugin = " ".join([letters[2*i]+letters[2*i+1] for i in range(10)])
myEnigma = enigma.Enigma(myReflector, *dayrotors, datekey, plugin)
ctx = myEnigma.encipher(text)
ciphers.append(ctx)


########################################################################## find key
def check(a,b):
    return all(i != j for i,j in zip(a,b))

for i in range(len(msg)-17):
    mykey = msg[i:i+17]

    for j in range(30):
        RIGHT = 1
        for cipher in ciphers:
            cpos = cipher[j:j+17]
            if(check(mykey, cpos) == False):
                RIGHT = 0
                break

        if(RIGHT == 1):
            print("possible_pos =", j, "possible_key =", mykey)

print(pos, key)

可以发现会有多个可能的key，说明密文组数还是不太够，但由于key显然是静态的，所以多次交互求个交集就可以了，最后可以得到key是：

1	key = "THEWEATHERTODAYIS"

恢复enigma的密钥

在拥有key的同时，我们也拥有了pos，所以现在我们现在拥有很多个明密文对如下：（数据只做示例用）

    THEWEATHERTODAYIS

RSQVJWPNHTWXTUYYXUSLJPHZZGSVEQJULPNTKEUKTSNLUTY
TBYWYJSPCWKTVJHMQPGYMLNFPOAHDVSIHNILKYSFKRKYLQB
BFDFWJIZGQKWZVBQRPJVHHDNNIKFYMNEOCGIQGZUWNOWBRY
BKZCZWYPYGHTLVZLEWZBDWXOWKKCAMARACMQFWNNVWJEMWX
FGQNJQCMMFFCTUBCWVDDGVUQGIQJSUEHCGBZCZJQSNMPEXF
MRKOZUUVFJMQSIBEMKQMZUGBZWTUPHJFHUFKKYJHTMGWBEK
AUUXGIQKPPDQPMXXIVKCQLVKIXGSQVOETMFSJJTHFPIFEPO
CVLGZCNZTRNEFAPSFMFUMKVKNOVIOJEMAKRMWHMGQNZLTKU
UEOSAUISNVEUFLNDIZHUDEZKUZHEVLNDBFOMCWXXHUXGUPL
GNSTEFKMSGZTYNASKBJUUASCFEAWQBNBVMDLWUGOXMXNLFE
IZGOPPYMQUGPCAIPXGFAFWZUKGWRZGRUBYGCCTRDCCPNFIO

然而每次enigma加密用的密钥三元组都是不一样的，也就是说这么多组明密文对，每组其实都对应一个不同的enigma机，我们只需要破解其中一台，就可以恢复完整text了。因此不妨选第一组做示例：

1
2
3

    THEWEATHERTODAYIS

RSQVJWPNHTWXTUYYXUSLJPHZZGSVEQJULPNTKEUKTSNLUTY

此时我们知道的明密文对应关系是：

1
2
3

----THEWEATHERTODAYIS--------------------------

----JWPNHTWXTUYYXUSLJ--------------------------

图灵把这种明密文对叫做一个crib，而我们现在要做的就是利用这个crib去破解这台enigma完全未知的密钥三元组，我们再回顾一下这三元组分别是什么，有多少种可能：

每次加密时有以下一些不同的配置，这些配置共同构成本次enigma加密的密钥：

五个rotors里面选取其中三个并作排列，如：IV、V、II

种数共有 $A(5,3) = 5 \cdot 4 \cdot 3 = 60$

每个被选中的rotor需要设置一个起始刻度，如：Q、V、M

种数共有 $26^3 = 17576$ 种

插线板需要选择十对字母两两组合，如：AB、CD、EF、GH、IJ、KL、MN、OP、QR、ST

种数共有 $\prod_{i=0}^{9}(\frac{26-2i}{2}) \approx 2^{69}$ 种

剩下没有配对的六个字母可以看作自己和自己交换(也就是不交换)，如：UU、VV、WW、XX、YY、ZZ

可以看出如果直接暴力求解的话，复杂度其实主要来自于plug的设置，如果已知plug的话，剩下要爆破的复杂度一共为：

$A(5,3) \cdot 26^3 = 1054560 \approx 2^{21}$

这就很容易接受了。

而图灵做的工作意义很重大，他做到的事情概括下来是：

假设给定一个或多个crib

crib肯定越多越好，越长越好，因为额外信息就更多
爆破密钥的前两个组成元素，也就是rotors和起始刻度
求出所有可能的plug设置

也就是说，图灵可以用2^21左右的可以接受的复杂度来求出少数的可能的plug，这就很厉害了。

效率很低的dfs

而其实这个工作的思路虽然说不容易想到，但图灵已经做出了成果，而理解这个成果其实并不难，核心思路就是剪枝+回溯，我们以刚才的crib做例子：

1
2
3

----THEWEATHERTODAYIS--------------------------

----JWPNHTWXTUYYXUSLJ--------------------------

我们爆破所有rotors和起始刻度，也就是我们除了plug的设置以外，当前的enigma已经可以跑起来了。那么对第一个字符T，我们知道其加密为了J，我们需要：

假设plug中的设置含有”TA”，那么T经过plug会到A
把A送进我们当前配置好的enigma进行加密，他会出来一个确定的字符，假设为B
B经过plug得到J，说明plug中一定也含有”BJ”

既然没有产生矛盾，那我们就继续向下推进一个字符，来到第二个字符H：

由于plug中每个字符仅能与一个字符配对，而此时A、B在刚才的推导中都出现过了，所以我们此时假设plug中含有”HC”
把C送进我们当前配置好的enigma进行加密，他会出来一个确定的字符，假设为T
T经过plug得到W，说明plug中一定也含有”TW”

此时就产生了矛盾，因为plug中每个字符仅能与一个字符配对，不会同时出现”TA”和”TW”。

这说明我们的假设中有地方出错了，那么我们就需要一层层向上回溯，而第一个回溯到的猜测点是”HC”，所以我们下面猜”HD”，然后如法炮制。

如果H和所有字母配对都会产生矛盾怎么办？这说明我们最开始猜测的”TA”就不对，那么我们就需要回溯到最开始，并猜测”TB”，然后往后进行。

如果T和所有字母配对都会产生矛盾怎么办？这说明一个事情：我们配置的enigma机出了问题，也就是说本次爆破的rotors和起始刻度是错误的，所以此时我们就该更换下一个待爆破的enigma机的配置，然后重复刚才的猜测-回溯过程了。

这一部分代码如下：

from pyenigma import rotor 
from string import ascii_uppercase
import random
from pyenigma import *
from itertools import *
from tqdm import *
from random import randint,choice,shuffle
import copy

########################################################################## data
myReflector=rotor.Reflector('WOEHCKYDMTFRIQBZNLVJXSAUGP',"myReflector")
myrotor1=rotor.Rotor('UHQAOFBEPIKZSXNCWLGJMVRYDT',"A",name="myrotor1")
myrotor2=rotor.Rotor('RIKHFBUJDNCGWSMZVXEQATOLYP',"A",name="myrotor2")
myrotor3=rotor.Rotor('ENQXUJSIVGOMRLHYCDKTPWAFZB',"A",name="myrotor3")
myrotor4=rotor.Rotor('JECGYWNDPQUSXZMKHRLTAVFOIB',"A",name="myrotor4")
myrotor5=rotor.Rotor('EYDBNSFAPJTMGURLOIWCHXQZKV',"A",name="myrotor5")
myrotors=[myrotor1,myrotor2,myrotor3,myrotor4,myrotor5]


key = "THEWEATHERTODAYIS"
letters = list(ascii_uppercase)
others = "".join([choice(letters) for i in range(30)])
pos = randint(0, len(others))
text = others[:pos]+key+others[pos:]
dayrotors = tuple(random.sample(myrotors, 3))
tmpkey = "".join([choice(letters) for i in range(3)])
shuffle(letters)
plugin = " ".join([letters[2*i]+letters[2*i+1] for i in range(10)])
myEnigma = enigma.Enigma(myReflector, *dayrotors, tmpkey, plugin)
ctx = myEnigma.encipher(text)


########################################################################## dfs
def check(plug):
    for i in ascii_uppercase:
        if(plug.count(i) >= 2):
            return False
    return True


def test(idx, rotors, XYZ, a, b, d, plug):
    temp_Enigma = enigma.Enigma(myReflector, *rotors, XYZ)
    temp_msg = "A"*idx + b
    c = (temp_Enigma.encipher(temp_msg))[-1]

    if(plug[ord(c)-ord("A")] == "*" or plug[ord(c)-ord("A")] == d):
        return c, True
    else:
        return c, False


def find(idx, rotors, XYZ, plug):
    if(check(plug) == False):
        return    
    if(idx == 17):
        print(plug)
        return

    temp_plug = copy.deepcopy(plug)

    a = pt[idx]
    d = ct[idx]
    if(plug[ord(a)-ord("A")] != "*"):
        b = plug[ord(a)-ord("A")]

        if(plug[ord(b)-ord("A")] != a and plug[ord(b)-ord("A")] != "*"):
            return
        
        c, res = test(idx, rotors, XYZ, a, b, d, plug)

        if(res == True):
            temp_plug[ord(a)-ord("A")] = b
            temp_plug[ord(b)-ord("A")] = a
            temp_plug[ord(c)-ord("A")] = d
            temp_plug[ord(d)-ord("A")] = c
            find(idx+1, rotors, XYZ, temp_plug)
    
    else:
        for b in ascii_uppercase:
            if(plug[ord(b)-ord("A")] != "*"):
                continue

            c, res = test(idx, rotors, XYZ, a, b, d, plug)

            if(res == True):
                temp_plug[ord(a)-ord("A")] = b
                temp_plug[ord(b)-ord("A")] = a
                temp_plug[ord(c)-ord("A")] = d
                temp_plug[ord(d)-ord("A")] = c
                find(idx+1, rotors, XYZ, temp_plug)

                temp_plug = copy.deepcopy(plug)

    return


########################################## show right plug config
if(1):
    right = ["*" for i in range(26)]
    for j in range(10):
        right[ord(plugin[3*j+0]) - ord("A")] = plugin[3*j+1]
        right[ord(plugin[3*j+1]) - ord("A")] = plugin[3*j+0]
    for i in range(26):
        if(right[i] == '*'):
            right[i] = chr(i+ord("A"))
    
    print(right)


########################################## data
pt = text
ct = ctx
key = "THEWEATHERTODAYIS"
plug = ["*" for i in range(26)]


########################################## assume we know the rotors and tmpkey
if(1):
    find(0, dayrotors, tmpkey, plug)


########################################## assume we don't know the rotors and tmpkey
if(0):
    length = 26**3
    for i in tqdm(product(letters,repeat=3), total=length):
        for j in permutations(myrotors,3):
            i = "".join(i)
            j = myrotors[:3]
            find(0, j, i, plug)

可以测试出来这样回溯找到正确plug的概率是相当高的，然而问题就在于：他太慢了。测一下要爆的时间得要40h-250h不等（和实际的crib本身结构有关）。

而本身德军用enigma，他们的密钥是一天一换的，所以就算放在当时，我现在写的脚本可能实时性都不够强XD，因此要换思路。

Turing’s method

而图灵用的是一种更巧妙的剪枝思路，具体来说他做了下面的事情：

我们仍然以刚才的crib为例：

1
2
3

----THEWEATHERTODAYIS--------------------------

----JWPNHTWXTUYYXUSLJ--------------------------

由于enigma的自反性，crib中的明密文可以在同样的配置下互相加密得到，所以可以先把crib的结构绘制成图：
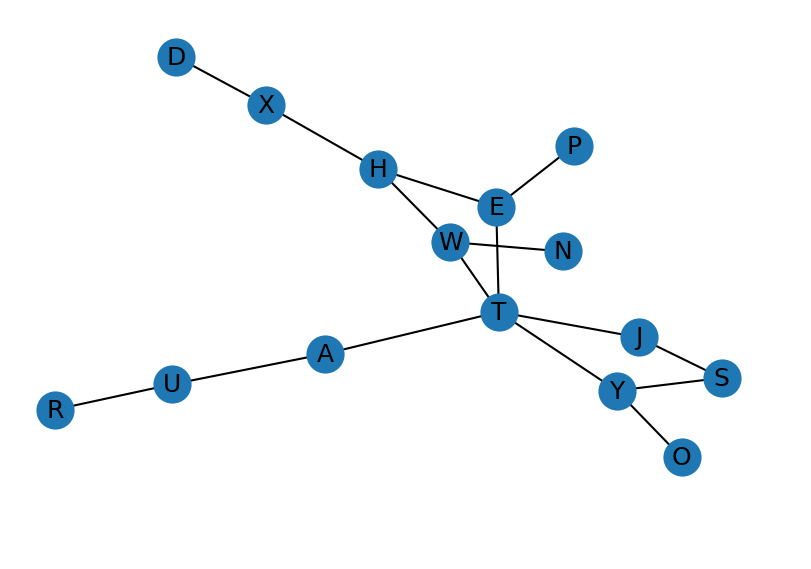
图中存在很特殊的结构，就是环，比如对于”TJSY”这个环，他是该段crib以下部分的明密文形成的：
1
2
3
----T---------T---Y-S--------------------------

----J---------Y---S-J--------------------------

利用crib中这种环结构，我们可以进一步简化我们的搜索思路。我们从环的任意一个节点开始，比如T，假设他经过plug变成A，那么此时在给定的配置下，我们可以畅通无阻的跑一遍这个环，直到他回到T，也就是：（小写的字母代表变量）

      ----T---------T---Y-S--------------------------
plugin    |         |   | |
      ----A---------r---q-p--------------------------
enigma    |         |   | |
      ----o---------q---p-o--------------------------
plugin    |         |   | |
      ----J---------Y---S-J--------------------------

为什么说畅通无阻呢？因为我们假设plugin存在”TA”后，假设A经过给定配置的enigma会得到o，那么plugin就一定会有”Jo”，o又可以用enigma跑出p，就一定有”Sp”，如此类推，最后从上图中的第二个链条可以得到一个”Tr”。

那么，按照我们的推断，这个r一定得是A才行，否则说明我们的推断出错了。

这个环结构的好处在于，我们绕过了J、Y、S的plugin设置，只需要讨论T的同时，就可以知道J、Y、S的哪些plugin设置才是合理的。
而又因为enigma的自反性，一旦推出矛盾项，可以说明整个逻辑链条上的所有plugin设置都是不合理的。比如我们以假设”TA”开始推测，一路推测出”RJ”、”SE”、”XY”，最后产生矛盾的”TB”，这代表”TA”、”RJ”、”SE”、”XY”、”TB”都一定是不合理的，所以我们下一次推测就不需要再讨论”TB”了，从”TC”开始就行。

然而对于一个环来说，即使我们当前爆破的enigma参数推的不正确，对于环依然是有一定概率存在字母，使得其不产生矛盾的。而这个概率直观来看也就是1/26。

而我们要爆破的enigma配置参数范围是：

$60 \cdot 26^3 = 1054560 \approx 2^{21}$

所以要想可能的plugin越少，就需要crib的环尽可能多，如果crib有三个环乃至四个环，那么得到的plugin就越少，就越可能正确。

因此如果从题目角度看，多roll一些crib，然后挑选其中环多一些的去爆破应该耗时会少很多，准确率也更高，用代码测试一下要roll到四个环及以上也并不需要太多次数：

from pyenigma import rotor 
from string import ascii_uppercase
from random import *
from pyenigma import *
from itertools import *
from tqdm import *
import networkx as nx


myReflector=rotor.Reflector('WOEHCKYDMTFRIQBZNLVJXSAUGP',"myReflector")
myrotor1=rotor.Rotor('UHQAOFBEPIKZSXNCWLGJMVRYDT',"A",name="myrotor1")
myrotor2=rotor.Rotor('RIKHFBUJDNCGWSMZVXEQATOLYP',"A",name="myrotor2")
myrotor3=rotor.Rotor('ENQXUJSIVGOMRLHYCDKTPWAFZB',"A",name="myrotor3")
myrotor4=rotor.Rotor('JECGYWNDPQUSXZMKHRLTAVFOIB',"A",name="myrotor4")
myrotor5=rotor.Rotor('EYDBNSFAPJTMGURLOIWCHXQZKV',"A",name="myrotor5")
myrotors=[myrotor1,myrotor2,myrotor3,myrotor4,myrotor5]


####################### find some rings
count1 = 0
while(1):
    ########################################################## gen
    letters = list(ascii_uppercase)
    key = "THEWEATHERTODAYIS"
    text = key
    dayrotors = [myrotors[0],myrotors[1],myrotors[2]]

    tmpkey = "".join([choice(letters) for i in range(3)])
    shuffle(letters)

    ttttt = [letters[2*i]+letters[2*i+1] for i in range(10)]
    plugin = " ".join(ttttt)
    for i in ascii_uppercase:
        if(i not in plugin):
            ttttt.append(i+i)
    myEnigma = enigma.Enigma(myReflector, *dayrotors, tmpkey, plugin)
    ctx = myEnigma.encipher(text)


    ########################################################## test 
    ############################################ find ring
    pt = text
    ct = ctx
    rings = []
    pair = [pt,ct]

    G = nx.Graph()
    G.add_edges_from([(pt[i],ct[i]) for i in range(17)])
    cycles = nx.simple_cycles(G)
    rings = []
    for i in cycles:
        rings.append(i)
    
    if(len(rings) >= 4):
        print(rings)
        print(count1)
        print(pt)
        print(ct)
        break

    count1 += 1

那么接下来就实现一下这种基于多环的dfs：

from pyenigma import rotor 
from string import ascii_uppercase
from random import *
from pyenigma import *
from itertools import *
from tqdm import *
import networkx as nx
import copy


myReflector=rotor.Reflector('WOEHCKYDMTFRIQBZNLVJXSAUGP',"myReflector")
myrotor1=rotor.Rotor('UHQAOFBEPIKZSXNCWLGJMVRYDT',"A",name="myrotor1")
myrotor2=rotor.Rotor('RIKHFBUJDNCGWSMZVXEQATOLYP',"A",name="myrotor2")
myrotor3=rotor.Rotor('ENQXUJSIVGOMRLHYCDKTPWAFZB',"A",name="myrotor3")
myrotor4=rotor.Rotor('JECGYWNDPQUSXZMKHRLTAVFOIB',"A",name="myrotor4")
myrotor5=rotor.Rotor('EYDBNSFAPJTMGURLOIWCHXQZKV',"A",name="myrotor5")
myrotors=[myrotor1,myrotor2,myrotor3,myrotor4,myrotor5]


####################### find some rings
count1 = 0
while(1):
    ########################################################## gen
    letters = list(ascii_uppercase)
    key = "THEWEATHERTODAYIS"
    text = key
    dayrotors = [myrotors[0],myrotors[1],myrotors[2]]

    tmpkey = "".join([choice(letters) for i in range(3)])
    shuffle(letters)

    plugin = " ".join([letters[2*i]+letters[2*i+1] for i in range(10)])
    myEnigma = enigma.Enigma(myReflector, *dayrotors, tmpkey, plugin)
    ctx = myEnigma.encipher(text)


    ########################################################## test 
    ############################################ find ring
    pt = text
    ct = ctx
    rings = []
    pair = [pt,ct]

    G = nx.Graph()
    G.add_edges_from([(pt[i],ct[i]) for i in range(17)])
    cycles = nx.simple_cycles(G)
    rings = []
    for i in cycles:
        rings.append(i)
    
    ####################### choose ring nums >= 10 to avoid collision
    if(len(rings) >= 8):
        if(0):
            print(rings)
            print(count1)
            print(pt)
            print(ct)
        break

    count1 += 1


########################################## add idx to ring
def add_idx_to_ring(ring):
    temp_ring = 2*ring
    idx_ring = []
    idx = 0
    temp_pair = temp_ring[0] + temp_ring[1]
    while(1):
        for i in range(17):
            if(pt[i] + ct[i] == temp_pair or pt[i] + ct[i] == temp_pair[::-1]):
                idx_ring.append([ring[idx],i])
                idx += 1
                temp_pair = temp_ring[idx] + temp_ring[idx+1]
                break
        if(len(idx_ring) == len(ring)):
            return idx_ring

idx_rings = []
for ring in rings:
    idx_rings.append(add_idx_to_ring(ring))
for i in range(len(idx_rings)):
    idx_rings[i] = idx_rings[i] + [idx_rings[i][0]]


########################################## dfs
def check(plug):
    for i in ascii_uppercase:
        if(plug.count(i) >= 2):
            return False
    return True

def record_bad_plug(plug):
    global bad_plug_dic
    for i,j in enumerate(plug):
        if(j == "*"):
            continue
        x,y = chr(i+ord("A")), j
        if(y in bad_plug_dic[x]):
            bad_plug_dic[x].remove(y)
        if(x in bad_plug_dic[y]):
            bad_plug_dic[y].remove(x)

def check_ring(a, b, ring, rotors, XYZ, plug):
    checkb = b
    temp_plug = copy.deepcopy(plug)

    temp_plug[ord(a)-ord("A")] = b
    temp_plug[ord(b)-ord("A")] = a

    pin = 0
    idx = ring[pin][1]

    while(1):
        temp_Enigma = enigma.Enigma(myReflector, *rotors, XYZ)
        temp_msg = "A"*idx + b
        c = (temp_Enigma.encipher(temp_msg))[-1]

        pin = pin + 1
        d = ring[pin][0]
        idx = ring[pin][1]
        b = c

        temp_plug[ord(c)-ord("A")] = d
        temp_plug[ord(d)-ord("A")] = c
        
        if(pin == len(ring) - 1):
            if(checkb == b):
                return True, temp_plug
            else:
                record_bad_plug(temp_plug)
                return False, temp_plug


def find(rings, plug ,rotors, XYZ):
    if(check(plug) == False):
        return
    
    if(rings == []):
        print(plug)
        return

    ring = rings[0]
    a = ring[0][0]

    temp_plug = copy.deepcopy(plug)

    if(plug[ord(a)-ord("A")] != "*"):
        b = plug[ord(a)-ord("A")]
        res, temp_plug = check_ring(a, b, ring, rotors, XYZ, temp_plug)
        if(res == True):
            find(rings[1:], temp_plug, rotors, XYZ)
            temp_plug = copy.deepcopy(plug)
        else:
            temp_plug = copy.deepcopy(plug)
            return
    
    else:
        temp = copy.deepcopy(bad_plug_dic[a])
        for b in temp:
            res, temp_plug = check_ring(a, b, ring, rotors, XYZ, temp_plug)
            if(res == True):
                find(rings[1:], temp_plug, rotors, XYZ)
            temp_plug = copy.deepcopy(plug)
    

########################################## show right plug config
if(1):
    right = ["*" for i in range(26)]
    for j in range(10):
        right[ord(plugin[3*j+0]) - ord("A")] = plugin[3*j+1]
        right[ord(plugin[3*j+1]) - ord("A")] = plugin[3*j+0]
    for i in range(26):
        if(right[i] == '*'):
            right[i] = chr(i+ord("A"))
    print(right)


plug = ["*" for i in range(26)]
########################################## assume we know the rotors and tmpkey
if(0):
    bad_plug_dic = {}
    for i in ascii_uppercase:
        bad_plug_dic[i] = [t for t in ascii_uppercase]
    find(idx_rings, plug, dayrotors, tmpkey)


########################################## assume we don't know the rotors and tmpkey
if(1):
    length = 26**3
    for i in tqdm(product(letters,repeat=3), total=length):
        for j in permutations(myrotors,3):
            bad_plug_dic = {}
            for tt in ascii_uppercase:
                bad_plug_dic[tt] = [t for t in ascii_uppercase]
            i = "".join(i)
            j = myrotors[:3]
            find(idx_rings, plug, j, i)

这个脚本耗时就相对来说能接受很多了，爆破完所有一般只需要一小时以内，对于赛题来说，不管是多进程还是直接多次交互赌一个起始刻度都可以控制时间在150s内。

注意两点：

上面控制了一直到roll出环数量大于等于8才开始搜索，不然可能的plugin会有点多。
最后得到的plugin貌似还是缺一些字符配对，不过我们可以有多种处理方式：
- 1.对有输出的rotors及配置，再进行一次刚才低效率的彻底的深搜
- 2.直接爆破剩余的字符，这个复杂度并不大

不得不说这个破译真的很艺术，奈何码力不够强，比赛中知道破译手段但是码不出来，还是要多练习。