糖醋小鸡块的blog
0%

Crypto趣题-古典密码

发表于 更新于 分类于 Valine：

该文章主要记录一些古典密码相关的趣题

Ex Viginere?

题目来源：MoeCTF 2021

加密流程解读

题目描述：

1
2
这难道是维吉尼亚吗？
text is a plain English text which only consists of lowercase letters (without any symbol)

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from random import randint
from secret import a, b, text, key, flag
from hashlib import*

table = 'abcdefghijklmnopqrstuvwxyz'
assert key in text
assert a * b < 100
assert flag == b'moectf{' + key.encode() + b'}'
assert md5(key.encode()+b'How_Interesting_the_Cryptography_Is').hexdigest() == '196cf7098c7ea6e3e4d03691fb9d4f58'

k1 = []
k2 = []

sequence = [0, 1]
n = randint(114514,1919810)
for i in range(65536):#2**16
    sequence.append((sequence[-1] + sequence[-2]) % n)

for i in range(a):
    k1.append(sequence[randint(0, 65536)] % 26)

for i in range(b):
    k2.append(sequence[randint(0, 65536)] % 26)

c = ''.join(table[((ord(x) - 97) * (k1[i % a]) + k2[i % b]) % 26] for i, x in enumerate(text))

f = open(r'./cipher','w')
f.write(c)
f.close()

并且给定cipher文件，其中内容为长度为108361的字母文本：

image-20230929101431427

把加密程序一点一点读完，可以提取出以下信息：

  • 最终 flag 由 key 组成，其中 key 是被加密的原文中的某个字符串
  • key 在原文中的位置未知，且长度未知
  • 生成一个随机数 n，作为之后生成 sequence 序列的模数
  • sequence 序列其实就是模 n 意义下的斐波那契数列，共生成 65536 项
  • 从 sequence 序列中随机选择 a 项并模 26，作为加密所需的 k1 序列
  • 从 sequence 序列中随机选择 b 项并模 26，作为加密所需的 k2 序列
  • 对原文中的每一个字符 m 进行仿射加密得到密文，其中仿射加密的 A 为 k1[i % a]，B 为 k2[i % b]

此外还有一些额外信息：

  • 一段有关 key 的md5值
  • a*b < 100

引入重合指数

因为密文很长，所以可以用统计方面的思想来解决题目，因此引入重合指数的概念：重合指数是指字符串中两个随机元素相同的概率。因此，假如我们仅考虑完全由英文字符组成的文本，那么一个文本的重合指数就按如下方式计算：(重合指数以 In 表示,p(a)表示 a 在文本中出现的频率)

1
In = p(a)*p(a) + p(b)*p(b) + p(c)*p(c) + ... + p(z)*p(z)

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
table = ascii_lowercase

#obj:待分割字符串  #sec:分割长度
def cut(obj, sec):
    return [obj[i:i+sec] for i in range(0,len(obj),sec)]

#计算重合指数
def In(c):
    freq = {i:0 for i in table}
    for i in range(len(table)):
        freq[table[i]] = c.count(table[i]) / len(c)
    index = 0
    for i in table:
        index += freq[i] * freq[i]
    return index

那么对于下列两种文本分别计算重合指数，就能看出它们的区别：(文本字符均足够多，符合统计概念)

1、完全随机的英文文本(26个字母均随机生成，因此出现频率相当，均为 1/26)

2、正常的英文文本(26个字符有使用频率上的差别)，一般来说如下：

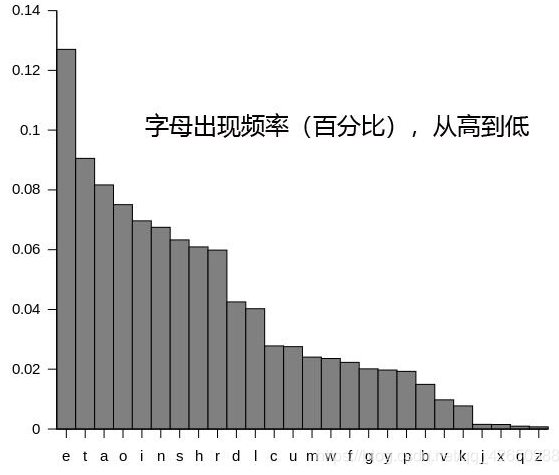
image-20230930103629784

1、

2、

由此，我们就有了一个区分随机文本与英文文本的重要依据。

解题

part1：找出密钥长度

重合指数如何应用到题目里呢？首先想明白一点：被同一个密钥(a、b均相同)加密的明文，一定会变成同一个密文。因此我们如果能够找到所有被同一个密钥加密的密文组，那么该密文组的重合指数是符合正常英文文本的(可以仔细想想)

所以我们就需要先由重合指数找到哪些密文是被同一个密钥加密的，实际上这就是在求 gcd(a,b) ,而由题目条件 a*b < 100，因此我们可以很快爆破出来：

1
2
3
4
5
6
7
8
9
10
11
#part1 依据重合指数找出a*b=77
t = c
if(1):
    for i in range(1,100):
        temp = cut(t,i)
        temp1 = ["" for m in range(i)]
        for k in range(len(temp)-1):
            temp1[0] += temp[k][0]
        index = In("".join(temp1[0]))
        if(index > 0.060):
            print("lenkey = ",i,"   In = ",index)

爆破得到a*b = 77，因此a=7，b=11或a=11，b=7

part2：确定密钥内容

确定了密钥长度后，现在就需要确定密钥的内容具体是什么，也就是 k1、k2里究竟是什么数字。

首先会发现一个 trick，那就是 sequence 序列的生成根本没什么用，由于最终是在mod 26 下进行计算，因此直接把sequence 当成一个由 0-25 组成的随机序列就可以。那么怎么确定呢，依然是利用重合指数，只是要换一种用法。

先引入一个结论：

假设 $ p1, p2 , p3…, pn$为递减的概率分布( $ p1\geq p2 \geq p3…\geq pn$ )，令$ q1’, q2’ , q3’…, qn’$为 $ q1, q2 , q3…, qn$的任意置换，则当 $ q1’, q2’ , q3’…, qn’$ 恰好也为递减的概率分布时，下式取得最大值：

这个结论的证明并不复杂，可以自行尝试。

这个结论有什么用呢？我们现在先把密文按长度为 77 分组，并取出每组的第一个字母组成一个新的密文串，那么这个新的密文串的所有字符，都是被k1[0]、k2[0]这个密钥加密的。那么我们爆破的密钥空间大小一共就只有12*26 = 312(参考仿射密码)。

爆破的依据是什么？仍然是重合指数，对于现在被加密的密文，它自身的重合指数是符合0.065的，因为是单表代换；但是加密过后，各个字符的频率发生了错位。比如正常英文文本中频率最高的是 e，而加密后可能变成了 z。那么把正常英文文本的概率分布当作p，把加密文本的概率分布当作q，就能发现可以利用刚才引入的结论来进行爆破了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#part2 依据与英语字频吻合指数找出具体的k1、k2
if(1):
    for i in range(11):
        for a in range(26):
            if GCD(a,26)!= 1 :
                continue
            for b in range(26):
                temp = cut(t,77)
                temp1 = ["" for m in range(77)]
                for k in range(len(temp)-1):
                    temp1[i] += temp[k][i]
                m = ''
                for x in temp1[i]:
                    m += table[((table.index(x)-b)*inverse(a,26))%26]
                index = In_m("".join(m))
                #print(index)
                if(index > 0.060):
                    print("a = ",a,"   b = ",b,",index = ",index)

之所以只爆破11个而不爆破全部77个，道理也很简单，爆破11个已经能够找出全部的k1、k2了。

part3：爆破md5

知道了密钥后就很轻松，就是个纯粹的爆破问题了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#part3 爆破密钥md5
if(1):
    m = ""
    k1 = [9,7,25,11,11,19,5,3,25,9,7]
    k2 = [25,19,18,19,25,20,8]
    a = 11
    b = 7
    for i in range(len(t)):
        temp = ((table.index(t[i])-k2[i%b])*inverse(k1[i%a],26))%26
        m += table[temp]

    Pad = b'How_Interesting_the_Cryptography_Is'
    MD5 = '196cf7098c7ea6e3e4d03691fb9d4f58'
    for i in range(30):
        for j in range(len(m)-i):
            key = m[j:j+i]
            if (md5(key.encode()+Pad).hexdigest() == MD5):
                print('moectf{'+key+'}')
                break

完整exp：(记得改一下if条件)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
from string import *
from Crypto.Util.number import *
from hashlib import *

with open(r'E:\vscode\cipher','r') as f:
    c = f.read()
f.close()

table = ascii_lowercase
dic = {'a': 0.08167,'b': 0.01492,'c': 0.02782,'d':0.04253,'e': 0.12702,'f':0.02228,'g': 0.02015,'h':0.06094,'i':0.06966,'j':0.00153,'k':0.00772,'l':0.04025,'m':0.02406,'n':0.06749,'o':0.07507,'p':0.01929,'q':0.00095,'r':0.05987,'s':0.06327,'t':0.09056,'u':0.02758,'v':0.00978,'w':0.02360,'x':0.00150,'y':0.01974,'z':0.00074}

#obj:待分割字符串  #sec:分割长度
def cut(obj, sec):
    return [obj[i:i+sec] for i in range(0,len(obj),sec)]

#计算重合指数
def In(c):
    freq = {i:0 for i in table}
    for i in range(len(table)):
        freq[table[i]] = c.count(table[i]) / len(c)
    index = 0
    for i in table:
        index += freq[i] * freq[i]
    return index

#计算与英语字频吻合指数
def In_m(c):
    freq = {i:0 for i in table}
    for i in range(len(table)):
        freq[table[i]] = c.count(table[i]) / len(c)
    index = 0
    for i in table:
        index += freq[i] * dic[i]
    return index

#part1 依据重合指数找出a*b=77
t = c
if(0):
    for i in range(1,100):
        temp = cut(t,i)
        temp1 = ["" for m in range(i)]
        for k in range(len(temp)-1):
            temp1[0] += temp[k][0]
        index = In("".join(temp1[0]))
        if(index > 0.060):
            print("lenkey = ",i,"   In = ",index)

#part2 依据与英语字频吻合指数找出具体的k1、k2
if(0):
    for i in range(11):
        for a in range(26):
            if GCD(a,26)!= 1 :
                continue
            for b in range(26):
                temp = cut(t,77)
                temp1 = ["" for m in range(77)]
                for k in range(len(temp)-1):
                    temp1[i] += temp[k][i]
                m = ''
                for x in temp1[i]:
                    m += table[((table.index(x)-b)*inverse(a,26))%26]
                index = In_m("".join(m))
                #print(index)
                if(index > 0.060):
                    print("a = ",a,"   b = ",b,",index = ",index)

#part3 爆破密钥md5
if(0):
    m = ""
    k1 = [9,7,25,11,11,19,5,3,25,9,7]
    k2 = [25,19,18,19,25,20,8]
    a = 11
    b = 7
    for i in range(len(t)):
        temp = ((table.index(t[i])-k2[i%b])*inverse(k1[i%a],26))%26
        m += table[temp]

    Pad = b'How_Interesting_the_Cryptography_Is'
    MD5 = '196cf7098c7ea6e3e4d03691fb9d4f58'
    for i in range(30):
        for j in range(len(m)-i):
            key = m[j:j+i]
            if (md5(key.encode()+Pad).hexdigest() == MD5):
                print('moectf{'+key+'}')
                exit()
                
#moectf{pieceofchocolate}

一个很纯粹的古典密码分析过程，其实是非常有意思也非常有价值的。



Unstable_time_machine

题目来源：暂不明确

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from sympy import totient,mobius
from tqdm import tqdm

secrets=b'xxx...xxx'

def Time_Machine(n):
    ans=0
    for k in tqdm(range(1,n+1)):
        for j in range(1,k+1):
            for i in range(1,j+1):
                ans+=j//i*(totient(i)+mobius(i))
    return ans

c=[]
for i in range(len(secrets)):
   c.append(Time_Machine(9999*secrets[i]))
print(c)

'''
[11827965311995932558558, 436740119853412116456, 41650252425798979676175, 50626127671556204573190, 41650252425798979676175, 60980101311350323854180, 963563059779422880492, 75413523978530416956915, 436740119853412116456, 43341417116799148415475, 86365877055447093121710, 65537436405378983697036, 43341417116799148415475, 40009068720753857066727, 75413523978530416956915, 436740119853412116456, 89280922053913796530170, 63227978177791478672610, 78047807265358355987991, 436740119853412116456, 75413523978530416956915, 63227978177791478672610, 436740119853412116456, 72846494790687055657395, 63227978177791478672610, 56664683419644282294873, 80750509186740318135738, 43341417116799148415475, 436740119853412116456, 58792701246489673616637, 89280922053913796530170, 436740119853412116456, 65537436405378983697036, 78047807265358355987991, 92269143789218304195771, 92269143789218304195771, 56664683419644282294873, 43341417116799148415475, 436740119853412116456, 36872675850292365936996, 48724893081131391463482, 43341417116799148415475, 36872675850292365936996, 41650252425798979676175, 436740119853412116456, 63227978177791478672610, 45083567393314209309726, 436740119853412116456, 75413523978530416956915, 50626127671556204573190, 58792701246489673616637, 43341417116799148415475, 1864884862832210879220, 436740119853412116456, 11827965311995932558558, 436740119853412116456, 43341417116799148415475, 86365877055447093121710, 65537436405378983697036, 43341417116799148415475, 40009068720753857066727, 75413523978530416956915, 436740119853412116456, 75413523978530416956915, 48724893081131391463482, 43341417116799148415475, 436740119853412116456, 65537436405378983697036, 70345565162259426664317, 63227978177791478672610, 46877717850904608344028, 70345565162259426664317, 36872675850292365936996, 58792701246489673616637, 436740119853412116456, 75413523978530416956915, 63227978177791478672610, 436740119853412116456, 70345565162259426664317, 78047807265358355987991, 60980101311350323854180, 436740119853412116456, 45083567393314209309726, 63227978177791478672610, 70345565162259426664317, 436740119853412116456, 89280922053913796530170, 43341417116799148415475, 36872675850292365936996, 70345565162259426664317, 72846494790687055657395, 1561103367493488746697, 8905422223361768646663, 7434854394795874666620, 19766534787409257458523, 8393017568869581586191, 20736491520823134042987, 10000251324957046694310, 95331756776933061303633, 89280922053913796530170, 2210983036628738475708, 78047807265358355987991, 33924401628947906025510, 54594963263249504183781, 60980101311350323854180, 2210983036628738475708, 83522804274246348745272, 33924401628947906025510, 75413523978530416956915, 50626127671556204573190, 58792701246489673616637, 43341417116799148415475, 33924401628947906025510, 40009068720753857066727, 2210983036628738475708, 58792701246489673616637, 65537436405378983697036, 56664683419644282294873, 43341417116799148415475, 86365877055447093121710, 50626127671556204573190, 75413523978530416956915, 89280922053913796530170, 33924401628947906025510, 80750509186740318135738, 43341417116799148415475, 70345565162259426664317, 89280922053913796530170, 33924401628947906025510, 83522804274246348745272, 43341417116799148415475, 2401069164267674760552, 2401069164267674760552, 493945107805384908948, 101685064551886104386625]
'''

题目内容很简单，给了一个Time_Machine()函数，然后对secret的每个字节乘上9999，再进行该函数运算，并给出函数值，要求还原secret。

预期解是拟合一个多项式去拟合，从而将函数内部的三层循环用一个拟合后的表达式直接算出，并与secret做对照得到flag。但是既然我将他分类到古典密码中，说明肯定有古典密码的做法，接下来就讲一讲这个做法。

首先要注意到一点，仔细观察这个函数：

1
2
3
4
5
6
7
def Time_Machine(n):
    ans=0
    for k in tqdm(range(1,n+1)):
        for j in range(1,k+1):
            for i in range(1,j+1):
                ans+=j//i*(totient(i)+mobius(i))
    return ans

三层循环，每层循环最内部其实都可以看作加上一个正数(mobius函数有可能为-1，但对加和的影响基本可以忽略不计)。也就是说，如果我们只关注Time_Machine()函数的自变量和返回值：

那么这个函数有一个很重要的性质：单调递增

这也就是说，对于secret中的每两个字符，如果第一个字符的ASCII码大于第二个字符，那么其乘9999后的函数值也会大于第二个字符。特殊一点，举几个在这题里面将会用到的一些例子就是：

那么接下来我们就根据这一点对secret进行分析。

统计频率

我们首先用如下程序统计出密文中每个数值出现次数：

1
2
3
4
tt = [11827965311995932558558, 436740119853412116456, 41650252425798979676175, 50626127671556204573190, 41650252425798979676175, 60980101311350323854180, 963563059779422880492, 75413523978530416956915, 436740119853412116456, 43341417116799148415475, 86365877055447093121710, 65537436405378983697036, 43341417116799148415475, 40009068720753857066727, 75413523978530416956915, 436740119853412116456, 89280922053913796530170, 63227978177791478672610, 78047807265358355987991, 436740119853412116456, 75413523978530416956915, 63227978177791478672610, 436740119853412116456, 72846494790687055657395, 63227978177791478672610, 56664683419644282294873, 80750509186740318135738, 43341417116799148415475, 436740119853412116456, 58792701246489673616637, 89280922053913796530170, 436740119853412116456, 65537436405378983697036, 78047807265358355987991, 92269143789218304195771, 92269143789218304195771, 56664683419644282294873, 43341417116799148415475, 436740119853412116456, 36872675850292365936996, 48724893081131391463482, 43341417116799148415475, 36872675850292365936996, 41650252425798979676175, 436740119853412116456, 63227978177791478672610, 45083567393314209309726, 436740119853412116456, 75413523978530416956915, 50626127671556204573190, 58792701246489673616637, 43341417116799148415475, 1864884862832210879220, 436740119853412116456, 11827965311995932558558, 436740119853412116456, 43341417116799148415475, 86365877055447093121710, 65537436405378983697036, 43341417116799148415475, 40009068720753857066727, 75413523978530416956915, 436740119853412116456, 75413523978530416956915, 48724893081131391463482, 43341417116799148415475, 436740119853412116456, 65537436405378983697036, 70345565162259426664317, 63227978177791478672610, 46877717850904608344028, 70345565162259426664317, 36872675850292365936996, 58792701246489673616637, 436740119853412116456, 75413523978530416956915, 63227978177791478672610, 436740119853412116456, 70345565162259426664317, 78047807265358355987991, 60980101311350323854180, 436740119853412116456, 45083567393314209309726, 63227978177791478672610, 70345565162259426664317, 436740119853412116456, 89280922053913796530170, 43341417116799148415475, 36872675850292365936996, 70345565162259426664317, 72846494790687055657395, 1561103367493488746697, 8905422223361768646663, 7434854394795874666620, 19766534787409257458523, 8393017568869581586191, 20736491520823134042987, 10000251324957046694310, 95331756776933061303633, 89280922053913796530170, 2210983036628738475708, 78047807265358355987991, 33924401628947906025510, 54594963263249504183781, 60980101311350323854180, 2210983036628738475708, 83522804274246348745272, 33924401628947906025510, 75413523978530416956915, 50626127671556204573190, 58792701246489673616637, 43341417116799148415475, 33924401628947906025510, 40009068720753857066727, 2210983036628738475708, 58792701246489673616637, 65537436405378983697036, 56664683419644282294873, 43341417116799148415475, 86365877055447093121710, 50626127671556204573190, 75413523978530416956915, 89280922053913796530170, 33924401628947906025510, 80750509186740318135738, 43341417116799148415475, 70345565162259426664317, 89280922053913796530170, 33924401628947906025510, 83522804274246348745272, 43341417116799148415475, 2401069164267674760552, 2401069164267674760552, 493945107805384908948, 101685064551886104386625]
dic = {i:0 for i in tt}
for i in tt:
    dic[i] += 1

打印出的结果为：

1
2
3
{11827965311995932558558: 2, 436740119853412116456: 18, 41650252425798979676175: 3, 50626127671556204573190: 4, 60980101311350323854180: 3, 963563059779422880492: 1, 75413523978530416956915: 9, 43341417116799148415475: 14, 86365877055447093121710: 3, 65537436405378983697036: 5, 40009068720753857066727: 3, 89280922053913796530170: 6, 63227978177791478672610: 7, 78047807265358355987991: 4, 72846494790687055657395: 2, 56664683419644282294873: 3, 80750509186740318135738: 2, 58792701246489673616637: 5, 92269143789218304195771: 
2, 36872675850292365936996: 4, 48724893081131391463482: 2, 45083567393314209309726: 2, 1864884862832210879220: 1, 70345565162259426664317: 6, 46877717850904608344028: 1, 1561103367493488746697: 1, 8905422223361768646663: 1, 7434854394795874666620: 1, 19766534787409257458523: 1, 8393017568869581586191: 1, 20736491520823134042987: 1, 10000251324957046694310: 1, 95331756776933061303633: 1, 2210983036628738475708: 3, 33924401628947906025510: 5, 54594963263249504183781: 1, 83522804274246348745272: 2, 2401069164267674760552: 2, 
493945107805384908948: 1, 101685064551886104386625: 1}

同时，打印出字典长度可以看到只有40个可见字符，然后secret长度却为135，说明有多个字符重复出现了，应该可以进行一点语义分析。

数值排序

然后，为了利用单调性，我们将字典中的键值对按数值顺序排好，如：

1
2
3
4
5
6
7
sequence = []
for i in sorted(dic.keys()) : 
    sequence.append((i, dic[i])) 
for i in range(len(sequence)):
    print(sequence[i],end = ",")
    if(i % 4 == 0):
        print()

每四个一行打印，主要是为了观察的方便，结果如下：

1
2
3
4
5
6
7
8
9
10
(436740119853412116456, 18),(493945107805384908948, 1),(963563059779422880492, 1),(1561103367493488746697, 1),
(1864884862832210879220, 1),(2210983036628738475708, 3),(2401069164267674760552, 2),(7434854394795874666620, 1),
(8393017568869581586191, 1),(8905422223361768646663, 1),(10000251324957046694310, 1),(11827965311995932558558, 2),
(19766534787409257458523, 1),(20736491520823134042987, 1),(33924401628947906025510, 5),(36872675850292365936996, 4),
(40009068720753857066727, 3),(41650252425798979676175, 3),(43341417116799148415475, 14),(45083567393314209309726, 2),
(46877717850904608344028, 1),(48724893081131391463482, 2),(50626127671556204573190, 4),(54594963263249504183781, 1),
(56664683419644282294873, 3),(58792701246489673616637, 5),(60980101311350323854180, 3),(63227978177791478672610, 7),
(65537436405378983697036, 5),(70345565162259426664317, 6),(72846494790687055657395, 2),(75413523978530416956915, 9),
(78047807265358355987991, 4),(80750509186740318135738, 2),(83522804274246348745272, 2),(86365877055447093121710, 3),
(89280922053913796530170, 6),(92269143789218304195771, 2),(95331756776933061303633, 1),(101685064551886104386625, 1)

词频分析

根据刚才的数值排序及频率列表，我们很快能确定以下几个字符：

1
" ","e","{","}"

这分别是因为：

  • 出现频率最高的值在数值排序中也在第一，所以应该是空格
  • 出现频率第二的值根据英语词频，应该是e
  • 大括号的ASCII码很靠后，因此最后两个应该就是左右大括号

所以我们第一步可以先手动赋一下这几个字符的初值：

1
2
3
4
dic_secret[436740119853412116456] = " "
dic_secret[43341417116799148415475] = "e"
dic_secret[101685064551886104386625] = "}"
dic_secret[95331756776933061303633] = "{"

然后，我们可以用以下函数将已知的字符代回原secret观察：

1
2
3
4
5
6
7
def output(dic_secret):
    for i in tt:
        try:
            print(dic_secret[i],end = "")
        except:
            print("*",end = "")
    print()

原secret此时如下：

1
* ****** e**e** *** ** ****e ** *****e **e** ** ***e* * e**e** **e ******* ** *** *** *e**********{************e******e******e****e***}

同时，我们把已知的几个字符插入数值序列中，就可以直观的看到数值大小顺序，函数如下：

1
2
3
4
5
6
7
def out_unknown(sequence,dic_secret):
    for i in sequence:
        if(i[0] in dic_secret.keys()):
            print(dic_secret[i[0]],end = "")
        else:
            print("*",end = "")
    print()

结果如下：

1
*****************e*******************{}

进一步分析

首先，由于知道flag头是DASCTF，那么我们其实就又可以确定六个字符，其对应结果如下：

1
2
3
* ****** e**e** *** ** ****e ** *****e **e** ** ***e* * e**e** **e ******* ** *** *** *e****DASCTF{************e******e******e****e***}

 ******ACDF*ST****e*******************{}

然后我们又已知，e后面应该全是小写字母了，我们不妨按倒序zyx….给他先排好，函数如下：

1
2
3
4
5
6
7
8
9
init = ord("z")
not_in_list = []
for i in range(len(sequence)-3,-1,-1):
    if(sequence[i][0] == 43341417116799148415475):
        break
    while(init in not_in_list):
        init -= 1
    dic_secret[sequence[i][0]] = chr(init)
    init -= 1

其中，not_in_list是为了去除接下来观察发现的多余字母，然后查看打印结果进行微调：

1
2
3
* *k*o*t exqe*t ypu tp spmve ny quzzme *je** ph tkne* * exqe*t tje qrpir*n tp ruo hpr ye*rs*DASCTF{y*u*lo*w*tkne***nqmexkty*very*we***}

 ******ACDF*ST****ehijklmnopqrstuvwxyz{}

可以看出有几个单词明显不对：

1
exqe*t ypu spmve tje...

那么就去除q，j这两个不应该出现的字母，重新打印：

1
2
3
4
5
6
7
8
9
10
11
12
13
init = ord("z")
not_in_list = [ord("q"),ord("j")]
for i in range(len(sequence)-3,-1,-1):
    if(sequence[i][0] == 43341417116799148415475):
        break
    while(init in not_in_list):
        init -= 1
    dic_secret[sequence[i][0]] = chr(init)
    init -= 1
   
* *i*n*t expe*t you to solve my puzzle *he** of time* * expe*t the progr*m to run for ye*rs*DASCTF{y*u*kn*w*time***mplexity*very*we***}

 ******ACDF*ST****efghiklmnoprstuvwxyz{}

可以发现这下明显合理多了，我们继续假设e前面的四个是小写字母(其实通过词频也可以看出这四个不会是大写字母)，继续打印观察结果，此时我们把break点调为大写T对应的数字：

1
2
3
4
5
6
7
8
9
10
11
12
13
init = ord("z")
not_in_list = [ord("q"),ord("j")]
for i in range(len(sequence)-3,-1,-1):
    if(sequence[i][0] == 20736491520823134042987):
        break
    while(init in not_in_list):
        init -= 1
    dic_secret[sequence[i][0]] = chr(init)
    init -= 1

* didn*t expect you to solve my puzzle bhebd of time* * expect the progrbm to run for yebrs*DASCTF{y*uakn*watimeac*mplexityaveryawe***}

 ******ACDF*STabcdefghiklmnoprstuvwxyz{}

显然可以判断出b不应该出现，加入到not_in_list中：

1
2
3
* didn*t expect you to solve my puzzle ahead of time* * expect the program to run for years*DASCTF{y*u`kn*w`time`c*mplexity`very`we***}

 ******ACDF*ST`acdefghiklmnoprstuvwxyz{}

此时基本上句子已经成型了，从语义已经可以推断剩下的字母，比如：

1
2
* didn*t
y*u

三个符号分别对应的是大写I，单引号’，数字0，然后进一步可以由ASCII码表确定最后几个字符，就能得到完整的secret了。

1
2
3
I didn't expect you to solve my puzzle ahead of time. I expect the program to run for years,DASCTF{y0u_kn0w_time_c0mplexity_very_we11!}

 !',.01ACDFIST_acdefghiklmnoprstuvwxyz{}

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
def out_sequence(sequence):
    for i in range(len(sequence)):
        print(sequence[i],end = ",")
        if(i % 4 == 3):
            print()

def output(dic_secret):
    for i in tt:
        try:
            print(dic_secret[i],end = "")
        except:
            print("*",end = "")
    print()

def out_unknown(sequence,dic_secret):
    for i in sequence:
        if(i[0] in dic_secret.keys()):
            print(dic_secret[i[0]],end = "")
        else:
            print("*",end = "")
    print()

tt = [11827965311995932558558, 436740119853412116456, 41650252425798979676175, 50626127671556204573190, 41650252425798979676175, 60980101311350323854180, 963563059779422880492, 75413523978530416956915, 436740119853412116456, 43341417116799148415475, 86365877055447093121710, 65537436405378983697036, 43341417116799148415475, 40009068720753857066727, 75413523978530416956915, 436740119853412116456, 89280922053913796530170, 63227978177791478672610, 78047807265358355987991, 436740119853412116456, 75413523978530416956915, 63227978177791478672610, 436740119853412116456, 72846494790687055657395, 63227978177791478672610, 56664683419644282294873, 80750509186740318135738, 43341417116799148415475, 436740119853412116456, 58792701246489673616637, 89280922053913796530170, 436740119853412116456, 65537436405378983697036, 78047807265358355987991, 92269143789218304195771, 92269143789218304195771, 56664683419644282294873, 43341417116799148415475, 436740119853412116456, 36872675850292365936996, 48724893081131391463482, 43341417116799148415475, 36872675850292365936996, 41650252425798979676175, 436740119853412116456, 63227978177791478672610, 45083567393314209309726, 436740119853412116456, 75413523978530416956915, 50626127671556204573190, 58792701246489673616637, 43341417116799148415475, 1864884862832210879220, 436740119853412116456, 11827965311995932558558, 436740119853412116456, 43341417116799148415475, 86365877055447093121710, 65537436405378983697036, 43341417116799148415475, 40009068720753857066727, 75413523978530416956915, 436740119853412116456, 75413523978530416956915, 48724893081131391463482, 43341417116799148415475, 436740119853412116456, 65537436405378983697036, 70345565162259426664317, 63227978177791478672610, 46877717850904608344028, 70345565162259426664317, 36872675850292365936996, 58792701246489673616637, 436740119853412116456, 75413523978530416956915, 63227978177791478672610, 436740119853412116456, 70345565162259426664317, 78047807265358355987991, 60980101311350323854180, 436740119853412116456, 45083567393314209309726, 63227978177791478672610, 70345565162259426664317, 436740119853412116456, 89280922053913796530170, 43341417116799148415475, 36872675850292365936996, 70345565162259426664317, 72846494790687055657395, 1561103367493488746697, 8905422223361768646663, 7434854394795874666620, 19766534787409257458523, 8393017568869581586191, 20736491520823134042987, 10000251324957046694310, 95331756776933061303633, 89280922053913796530170, 2210983036628738475708, 78047807265358355987991, 33924401628947906025510, 54594963263249504183781, 60980101311350323854180, 2210983036628738475708, 83522804274246348745272, 33924401628947906025510, 75413523978530416956915, 50626127671556204573190, 58792701246489673616637, 43341417116799148415475, 33924401628947906025510, 40009068720753857066727, 2210983036628738475708, 58792701246489673616637, 65537436405378983697036, 56664683419644282294873, 43341417116799148415475, 86365877055447093121710, 50626127671556204573190, 75413523978530416956915, 89280922053913796530170, 33924401628947906025510, 80750509186740318135738, 43341417116799148415475, 70345565162259426664317, 89280922053913796530170, 33924401628947906025510, 83522804274246348745272, 43341417116799148415475, 2401069164267674760552, 2401069164267674760552, 493945107805384908948, 101685064551886104386625]
dic = {i:0 for i in tt}
for i in tt:
    dic[i] += 1

sequence = []
for i in sorted(dic.keys()) : 
    sequence.append((i, dic[i])) 
#out_sequence(sequence)


#init
dic_secret = {}
dic_secret[436740119853412116456] = " "
dic_secret[43341417116799148415475] = "e"
dic_secret[101685064551886104386625] = "}"
dic_secret[95331756776933061303633] = "{"
dic_secret[7434854394795874666620] = "A"
dic_secret[8393017568869581586191] = "C"
dic_secret[8905422223361768646663] = "D"
dic_secret[10000251324957046694310] = "F"
dic_secret[19766534787409257458523] = "S"
dic_secret[20736491520823134042987] = "T"


init = ord("z")
not_in_list = [ord("q"),ord("j"),ord("b")]
for i in range(len(sequence)-3,-1,-1):
    if(sequence[i][0] == 20736491520823134042987):
        break
    while(init in not_in_list):
        init -= 1
    dic_secret[sequence[i][0]] = chr(init)
    init -= 1

#final
dic_secret[436740119853412116456] = " "
dic_secret[493945107805384908948] = "!"
dic_secret[963563059779422880492] = "\'"
dic_secret[1561103367493488746697] = ","
dic_secret[1864884862832210879220] = "."
dic_secret[2210983036628738475708] = "0"
dic_secret[2401069164267674760552] = "1"

dic_secret[11827965311995932558558] = "I"
dic_secret[33924401628947906025510] = "_"

output(dic_secret)
out_unknown(sequence,dic_secret)

#DASCTF{y0u_kn0w_time_c0mplexity_very_we11!}